Cat Swarm Optimization
Last Updated :
28 Nov, 2022
Nature is replete with social compartments to carry out various jobs. Even if the final goal of all persons and collective conduct is survival, for various reasons: hunting, protection, navigation and foraging animals work and interact in groups, herds, schools, colonies and flocks. It is very interesting that creatures find the optimal situations and perform tasks efficiently in groups. It is clear that such optimal and efficient conduct has been evolved throughout the millennia. So we inspire them to fix our issues is fairly logical. This is the main aim of a study field called swarm intelligence (SI). Many algorithms have been proposed in the field of swarm intelligence (SI) e.g. Ant Colony Optimization (ACO), Particle Swarm Optimization (PSO), Grey Wolf Optimizer (GWO) etc.
In this article, we shall discuss the Cat Swarm Optimization technique which is a swarm-based optimization.
Inspiration:
Cat Swarm Optimization is clearly inspired by the behaviour of cats in the real world. According to biology, there are about 32 different cat species from lions to cheetahs and from tigers to domestic cats. Even though they live in quite different environments many behavioural attributes are similar. Despite being in most times inactive, cats have a strong curiosity.
Before defining the mathematical model of the algorithm, one must know that there are two different states of being for any cat.
- Seeking mode: Cats are inactive in this state i.e. resting, looking around or in a state to move to another location.
- Tracking mode: Cats are active in this state i.e. they change their current position.
Mathematical Model:
Let’s define the model of cat swarm optimization. Every cat in a solution space has its own N dimensions dN, velocity for each dimension 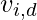 , a flag that suggests whether the cat is in either of the two modes (seeking or tracking) and finally a fitness value that represents the accommodation of cats to the fitness function.
, a flag that suggests whether the cat is in either of the two modes (seeking or tracking) and finally a fitness value that represents the accommodation of cats to the fitness function.
We desire to find the optimal position for a cat.
Seeking mode: As already mentioned cats in this state are inactive. This mode has four essential factors namely: seeking memory pool (SMP), seeking a range of the selected dimension (SRD), counts of dimension to change (CDC), and self-position considering (SPC).
- SMP: Defines the memory for each cat indicating the points pursued by a cat.
- SRD: declares the mutative ratio for the selected dimensions.
- CDC: How many dimensions will be varied is indicated by this factor.
- SPC: Whether the position at which the cat is already placed will be a candidate point for a cat to move to. It is a Boolean value (either true or false).
NOTE: Regardless of the value of SPC the value of SMP is not influenced.
1. If SPC is True Then
j=SMP
Else
j=SMP-1
2. Present position of cat Ck is copied j times.
3. Depending on the value of CDC the value of SRD is either decremented or incremented.
4. Calculate the Fitness value (FV) of all candidate points.
5. If all the FV are not equal, FV are converted to selection probability:
 where i ranges in (0,j)
where i ranges in (0,j) 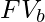 can be set to
can be set to 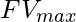 or
or 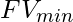 depending on the goal of fitness function either maximize or minimize. 6. Randomly select the candidate points and replace the current position of cat Ck.
depending on the goal of fitness function either maximize or minimize. 6. Randomly select the candidate points and replace the current position of cat Ck.
Tracing mode: Once a cat is in tracing mode, the cat is assigned with its velocity as 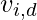 .
.
1. Update the velocities of each cat according to:
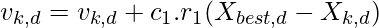 where d ranges in [1,N]
where d ranges in [1,N] 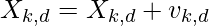 c1 is a constant, r1 ranges in [0,1] and
c1 is a constant, r1 ranges in [0,1] and 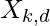 and
and 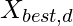 are the position of cat Ck in dimension d and the position of a cat with the best FV respectively.2. If
are the position of cat Ck in dimension d and the position of a cat with the best FV respectively.2. If  Then
Then  Else
Else 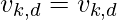
CSO algorithm
In order to merge both the modes, we must keep in mind that the cats spend most of the time in seeking mode. Therefore, we define a mixture ratio (MR) that suggests how much of either of the modes to take into account while performing CSO. It is quite evident that we must keep the value of MR very low to account for cats spending the most time in seeking mode.
1. Create M cats.
2. Randomly drop the M cats in N dimensional solution space. Assign the velocities of each cat in
accordance to 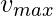 .3. Distribute the cats to tracing mode according to MR and rest to seeking mode.4. Apply the position of the cat
.3. Distribute the cats to tracing mode according to MR and rest to seeking mode.4. Apply the position of the cat 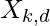 into the fitness function and calculate the fitness value FV.5. Move the cats according to their flag value. If Ck is in tracing mode apply the tracing mode process to it, if not then apply seeking mode process.6. Redistribute the cats according to MR.7. Repeat from step 4 to 6 until termination condition is met.
into the fitness function and calculate the fitness value FV.5. Move the cats according to their flag value. If Ck is in tracing mode apply the tracing mode process to it, if not then apply seeking mode process.6. Redistribute the cats according to MR.7. Repeat from step 4 to 6 until termination condition is met.
By applying the CSO we get the 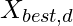 which is the position of a cat with the best FV.
which is the position of a cat with the best FV.
This is how the CSO algorithm works.
Reference:
https://link.springer.com/chapter/10.1007/978-3-540-36668-3_94
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...