Partial Least Squares Singular Value Decomposition (PLSSVD)
Last Updated :
25 Oct, 2023
Partial Least Squares Singular Value Decomposition (PLSSVD) is a sophisticated statistical technique employed in the realms of multivariate analysis and machine learning. This method merges the strengths of Partial Least Squares (PLS) and Singular Value Decomposition (SVD), offering a powerful tool to extract crucial information from high-dimensional data while effectively mitigating issues like multicollinearity and noise.
Partial Least Squares (PLS)
Partial Least Squares Singular Value Decomposition (PLSSVD)
PLSSVD is a variant of PLS that uses singular value decomposition (SVD) to extract the latent variables from X.
SVD is a matrix factorization technique that decomposes a matrix into three simpler matrices: U, Σ (Sigma), and V.
The PLSSVD algorithm can be summarized in the following steps:
- Perform SVD on the predictor matrix X.
- Calculate the weight vector, w, as the first column of the right singular vector matrix V.
- Calculate the scores, t, as the linear combination of X using w.
- Calculate the loading vector, p, as the weights for the original variables in X.
- Update X and Y by removing the explained variance.
- Repeat steps 2-5 until the desired number of latent variables are extracted.
The PLS model can then be used to predict Y for new observations by simply calculating the linear combination of the latent variables for those observations.
Mathematical Explanation of PLSSVD
- The PLSSVD algorithm can be expressed mathematically as follows:
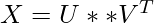
![Rendered by QuickLaTeX.com w = V[:, 0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fc603f41807b9ccd758725ffa216bce2_l3.png)
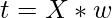
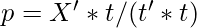
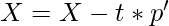
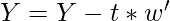
- Repeat steps 2-6 until the desired number of latent variables are extracted.
- Once the latent variables have been extracted, the PLS model can be used to predict Y for new observations using the same equation as for PLS.
Similarities and Differences between PCA and PLSSVD
Similarities:
- Both Principal Component Analysis (PCA) and PLSSVD are dimensionality reduction techniques.
- They aim to capture the most important information in high-dimensional data.
- Dimensionality Reduction: Both PCA and PLS-SVD are techniques used to reduce the dimensionality of high-dimensional data. They aim to capture the most important information while reducing the number of variables.
- Orthogonal Transformations: Both methods use orthogonal transformations to achieve dimensionality reduction. In PCA, the principal components are orthogonal to each other, and in PLS-SVD, the latent variables are orthogonal components.
- Linear Techniques: PCA and PLS-SVD are linear techniques, meaning they work well when relationships between variables are primarily linear.
Differences:
- Objective:
- PCA: PCA aims to maximize the variance in the data. It identifies new orthogonal axes (principal components) such that the data’s variance is maximized along these axes. PCA is an unsupervised technique and does not consider any specific relationship with a target variable.
- PLS-SVD: PLS-SVD focuses on maximizing the covariance between the predictor variables (X) and the response variable (Y). It identifies latent variables that explain both the variance in X and its covariance with Y. PLS-SVD is a supervised technique and is specifically designed for modeling relationships between X and Y.
- Use Case:
- PCA: PCA is often used for data compression, noise reduction, and visualization. It’s useful for exploring the intrinsic structure of data, clustering, and reducing the dimensionality of features.
- PLS-SVD: PLS-SVD is used when there is a predictive relationship between X and Y, such as in regression or classification tasks. It’s employed to find components in X that are relevant for predicting Y. PLS-SVD is particularly beneficial when dealing with multicollinearity or when you want to maximize predictive power.
- Output:
- PCA: The output of PCA includes principal components, which are linear combinations of the original variables. These components are ordered by their explained variance.
- PLS-SVD: The output of PLS-SVD includes latent variables, which are also linear combinations of the original variables. These latent variables are chosen to maximize the covariance between X and Y.
- Uniqueness of Components:
- PCA: Each principal component is unique and orthogonal to others. They capture the maximum variance in the data.
- PLS-SVD: Latent variables are not necessarily unique; multiple sets of latent variables can be derived to maximize covariance between X and Y, depending on the problem’s complexity.
PLS-SVD Related Concepts
Multicollinearity:
- When two or more independent variables in a regression model are significantly associated, multicollinearity develops.
- PLS-SVD handles multicollinearity by generating latent variables that represent the greatest possible covariance between predictor factors and response variables.
Latent Variables:
- PLS-SVD constructs unobservable variables to describe underlying patterns in the data.
- These latent variables are linear combinations of the original variables.
Singular Value Decomposition (SVD):
- In PLS-SVD, SVD is a matrix factorization technique that decomposes data matrices into orthogonal components.
- It aids in the identification of latent variables that maximize the covariance between predictor and response variables.
Regression and Classification:
- PLS-SVD can be used for regression tasks to predict continuous target variables and for classification tasks to predict categorical target variables.
Syntax of class PLSSVD
In scikit-learn (sklearn), the PLSSVD class can be found in the sklearn.cross_decomposition module.
Here’s the syntax:
sklearn.cross_decomposition.PLSSVD(n_components=2, *, scale=True, copy=True)
Parameters:
- n_components: The number of latent variables (components) to compute.
- scale: A Boolean flag indicating whether to scale X and Y before modeling. Scaling is often important to ensure proper analysis when the scales of variables differ
You can adjust the n_components parameter based on your specific analysis needs to control the dimensionality of the latent variables generated by the PLSSVD algorithm. The scale parameter determines whether your data should be mean-centered and scaled before applying PLSSVD. This preprocessing step can be crucial, especially when dealing with datasets with variables of varying scales.
Steps to Perform Partial Least Squares Singular Value Decomposition (PLS-SVD)
Consider the following scenario: you want to forecast the alcohol concentration of wine based on several chemical properties. You’ll utilize PLS-SVD to build latent variables that represent the underlying relationships between these qualities and alcohol content.
Import Libraries:
Import the necessary libraries, including scikit-learn (sklearn).
Python3
from sklearn.cross_decomposition import PLSRegression
from sklearn.datasets import load_wine
import matplotlib.pyplot as plt
|
Prepare Your Data:
- Sort your information into predictor variables (X) and target variables (y).
Python
wine = load_wine()
X = wine.data
y = wine.target
|
Instantiate PLS-SVD Model:
- Create an instance of the PLSRegression model.
- n_components specifies the number of latent variables (components) to compute.
Python3
pls = PLSRegression(n_components=2)
|
Fit the Model:
- Fit the PLS-SVD model to your data.
Transform Data:
- Use the transform method to compute the latent variables.
Python3
X_latent = pls.transform(X)
|
Visualization Results:
- Examine the latent variables to understand the relationships between your predictor variables and the target variable.
Python3
plt.scatter(X_latent[:, 0], X_latent[:, 1], c=y, cmap='viridis')
plt.xlabel('Latent Variable 1')
plt.ylabel('Latent Variable 2')
plt.title('PLS-SVD Latent Variables')
plt.colorbar(label='Alcohol Content')
plt.show()
|
Output:
.png)
PLS-SVD has developed two latent variables in this case that represent the correlations between chemical characteristics and alcohol concentration in wine. The scatter plot depicts how these latent variables aid in differentiating between levels of alcohol concentration in the wine dataset.
Applications of PLS-SVD:
Below are some of the key applications of PLS-SVD:
- Regression Analysis: PLS-SVD is commonly used in regression analysis, particularly in cases where there are multiple predictor variables (X) and one or more response variables (Y). It helps identify latent variables (components) in X that have the highest covariance with Y, making it effective for modeling complex relationships.
- Classification: In addition to regression, PLS-SVD can be applied to classification tasks. It helps reduce the dimensionality of the feature space while preserving the information necessary for accurate classification. This is especially valuable when dealing with high-dimensional data and the risk of overfitting.
- Image Processing: PLS-SVD can be used for image compression and denoising. By capturing the most significant components of an image, it helps reduce storage requirements and improve image quality.
- Quality Control: PLS-SVD plays a role in quality control and process optimization in manufacturing industries. It helps detect deviations from desired product specifications and suggests adjustments to maintain product quality.
- Market Research: PLS-SVD is used in market research to analyze customer surveys and feedback data. It helps identify underlying factors that influence customer preferences and purchasing behavior.
- Financial Modeling: PLS-SVD can be employed in financial modeling to analyze financial time series data and identify latent factors that influence asset prices and market movements.
These are just a few examples of the diverse range of applications for PLS-SVD. Its ability to handle high-dimensional, noisy, and correlated data while capturing underlying patterns and relationships makes it a valuable tool in various domains.
Share your thoughts in the comments
Please Login to comment...