Orthogonal Projections
Last Updated :
16 Oct, 2021
Orthogonal Sets:
A set of vectors 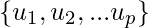 in
in 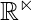 is called orthogonal set, if
is called orthogonal set, if  . if
. if 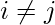
Orthogonal Basis
An orthogonal basis for a subspace W of  is a basis for W that is also an orthogonal set.
is a basis for W that is also an orthogonal set.
Let S = 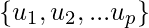 be the orthogonal basis for a W of
be the orthogonal basis for a W of 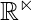 is a basis for W that is also a orthogonal set. We need to calculate
is a basis for W that is also a orthogonal set. We need to calculate 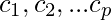 such that :
such that :
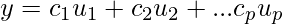
Let’s take the dot product of u_1 both side.
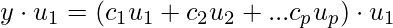
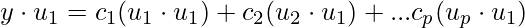
Since, this is orthogonal basis 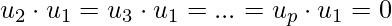 . This gives
. This gives 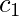 :
:
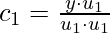
We can generalize the above equation

Orthogonal Projections
Suppose {u_1, u_2,… u_n} is an orthogonal basis for W in 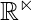 . For each y in W:
. For each y in W:

Let’s take 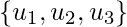 is an orthogonal basis for
is an orthogonal basis for 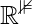 and W = span
and W = span 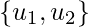 . Let’s try to write a write y in the form
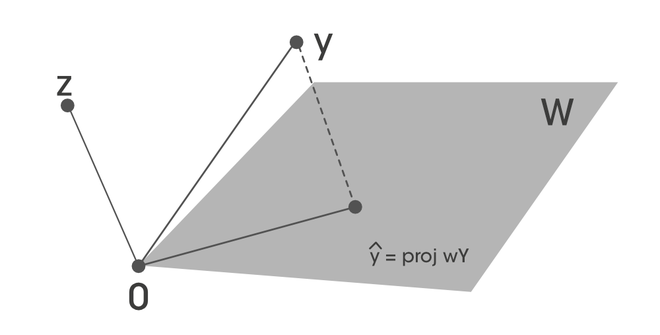
. Let’s try to write a write y in the form 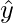 belongs to W space, and z that is orthogonal to W.
belongs to W space, and z that is orthogonal to W.
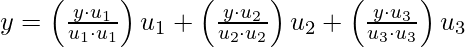
where

and
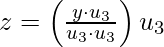 [Tex]y= \hat{y} + z[/Tex]
[Tex]y= \hat{y} + z[/Tex]
Now, we can see that z is orthogonal to both 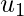 and
and 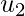 such that:
such that:
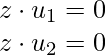

Orthogonal Decomposition Theorem:
Let W be the subspace of 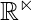 . Then each y in
. Then each y in 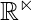 can be uniquely represented in the form:
can be uniquely represented in the form:
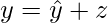
where 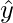 is in W and z in W^{\perp}. If
is in W and z in W^{\perp}. If 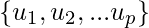 is an orthogonal basis of W. then,
is an orthogonal basis of W. then,
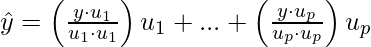
thus:
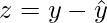
Then, 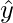 is the orthogonal projection of y in W.
is the orthogonal projection of y in W.
Best Approximation Theorem
Let W is the subspace of 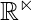 , y any vector in
, y any vector in 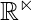 . Let v in W and different from
. Let v in W and different from 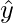 . Then
. Then 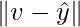 also in W.
also in W.
 is orthogonal to W, and also orthogonal to
is orthogonal to W, and also orthogonal to 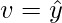 . Then y-v can be written as:
. Then y-v can be written as:
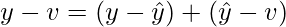
Thus:
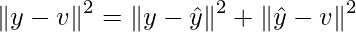
Thus, this can be written as:
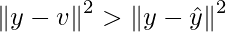
and
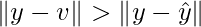

References:
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...