Ordered Prime Signature
Last Updated :
03 Aug, 2022
Given a number n, find the ordered prime signatures and using this find the number of divisor of given n.
Any positive integer, ‘n’ can be expressed in the form of its prime factors. If ‘n’ has p1, p2, … etc. as its prime factors, then n can be expressed as :
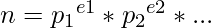
Now, arrange the obtained exponents of the prime factors of ‘n’ in non-decreasing order. The arrangement thus obtained is called the ordered prime signature of the positive integer ‘n’.
Example:
Input : n = 20
Output :
The Ordered Prime Signature of 20 is :
{ 1, 2 }
The total number of divisors of 20 is 6
Input : n = 13
Output :
The Ordered Prime Signature of 13 is :
{ 1 }
The total number of divisors of 13 is 2
Explanation :
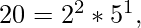 ordered prime signature of 20 = { 1, 2 }
ordered prime signature of 20 = { 1, 2 }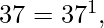 ordered prime signature of 37 = { 1 }
ordered prime signature of 37 = { 1 }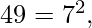 ordered prime signature of 49 = { 2 }
ordered prime signature of 49 = { 2 }
It can be ascertained from the above discussion that the prime signature of 1 is { 1 }. Furthermore, all prime numbers have the same signature, i.e { 1 } and the prime signature of a number, that is the k-th power of a prime number (say, 25 which is the 2-nd power of 5), is always { k }.
For example :
Ordered Prime signature of 100 = { 2, 2 }, as 100 = 2^2 × 5^2
Now adding one to each element gives { 3, 3 } and the product is 3 × 3 = 9,
i.e the total number of divisors of 100 is nine.
They are 1, 2, 4, 5, 10, 20, 25, 50, 100.
Approach :
1) Find the prime factorization of the number
2) Store each exponent corresponding to a prime factor, in a vector
3) Sort the vector in ascending order
4) Add one to each element present in the vector
5) Multiply all the elements
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> primes(int n)
{
bool prime[n + 1];
memset(prime, true, sizeof(prime));
for (int i = 2; i * i <= n; i++)
{
if (prime[i] == true) {
for (int j = i * 2; j <= n; j += i)
prime[j] = false;
}
}
vector<int> arr;
for (int i = 2; i <= n; i++)
{
if (prime[i])
arr.push_back(i);
}
return arr;
}
vector<int> signature( int n)
{
vector<int> r = primes(n);
map<int, int> factor;
map<int, int>::iterator it;
vector<int> sort_exp;
int k, t = n;
it = factor.begin();
for (int i = 0; i < r.size(); i++)
{
if (n % r[i] == 0) {
k = 0;
while (n % r[i] == 0) {
n = n / r[i];
k++;
}
factor.insert(it, pair<int, int>(r[i], k));
sort_exp.push_back(k);
}
}
sort(sort_exp.begin(), sort_exp.end());
cout << " The Ordered Prime Signature of " <<
t << " is : \n{ ";
for (int i = 0; i < sort_exp.size(); i++)
{
if (i != sort_exp.size() - 1)
cout << sort_exp[i] << ", ";
else
cout << sort_exp[i] << " }\n";
}
return sort_exp;
}
void divisors(int n)
{
int f = 1, l;
vector<int> div = signature(n);
l = div.size();
for (int i = 0; i < l; i++)
{
div[i] += 1;
f *= div[i];
}
cout << "The total number of divisors of " <<
n << " is " << f << "\n";
}
int main()
{
int n = 13;
divisors(n);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static class pair
{
int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
static Vector<Integer> primes(int n)
{
boolean []prime = new boolean[n + 1];
Arrays.fill(prime, true);
for (int i = 2; i * i <= n; i++)
{
if (prime[i] == true) {
for (int j = i * 2; j <= n; j += i)
prime[j] = false;
}
}
Vector<Integer> arr = new Vector<>();
for (int i = 2; i <= n; i++)
{
if (prime[i])
arr.add(i);
}
return arr;
}
static Vector<Integer> signature( int n)
{
Vector<Integer> r = primes(n);
HashMap<Integer,Integer> factor = new HashMap<>();
Vector<Integer> sort_exp = new Vector<>();
int k, t = n;
int it = 0;
for (int i = 0; i < r.size(); i++)
{
if (n % r.get(i) == 0)
{
k = 0;
while (n % r.get(i) == 0)
{
n = n / r.get(i);
k++;
}
factor.put(r.get(i), k);
sort_exp.add(k);
}
}
Collections.sort(sort_exp);
System.out.print(" The Ordered Prime Signature of " +
t+ " is : \n{ ");
for (int i = 0; i < sort_exp.size(); i++)
{
if (i != sort_exp.size() - 1)
System.out.print(sort_exp.get(i) + ", ");
else
System.out.print(sort_exp.get(i) + " }\n");
}
return sort_exp;
}
static void divisors(int n)
{
int f = 1, l;
Vector<Integer> div = signature(n);
l = div.size();
for (int i = 0; i < l; i++)
{
f *= (div.get(i) + 1);
}
System.out.print("The total number of divisors of " +
n + " is " + f + "\n");
}
public static void main(String[] args)
{
int n = 13;
divisors(n);
}
}
|
Python3
def primes(n):
prime = [True for _ in range(n + 1)]
for i in range(2, int(n ** 0.5) + 1):
if (prime[i] == True):
for j in range(2 * i, n + 1, i):
prime[j] = False
arr = []
for i in range(2, n + 1):
if (prime[i]):
arr.append(i)
return arr
def signature(n):
r = primes(n)
factor = dict()
sort_exp = []
t = n
for i in range(len(r)):
if (n % r[i] == 0):
k = 0
while (n % r[i] == 0):
n //= r[i]
k = k + 1
factor[r[i]] = k
sort_exp.append(k)
sort_exp.sort()
print(" The Ordered Prime Signature of ", t, " is :")
print("{", end=" ")
for i in range(len(sort_exp)):
if (i != len(sort_exp) - 1):
print(sort_exp[i], end=", ")
else:
print(sort_exp[i], "}")
return sort_exp
def divisors(n):
f = 1
div = signature(n)
l = len(div)
for i in range(l):
div[i] += 1
f *= div[i]
print("The total number of divisors of ", n, " is ", f)
n = 13
divisors(n)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static List<int> primes(int n)
{
bool []prime = new bool[n + 1];
for (int i = 0; i < n + 1; i++)
prime[i] = true;
for (int i = 2; i * i <= n; i++)
{
if (prime[i] == true)
{
for (int j = i * 2;
j <= n; j += i)
prime[j] = false;
}
}
List<int> arr = new List<int>();
for (int i = 2; i <= n; i++)
{
if (prime[i])
arr.Add(i);
}
return arr;
}
static List<int> signature( int n)
{
List<int> r = primes(n);
var factor = new Dictionary<int, int>();
List<int> sort_exp = new List<int>();
int k, t = n;
for (int i = 0; i < r.Count; i++)
{
if (n % r[i] == 0)
{
k = 0;
while (n % r[i] == 0)
{
n = n / r[i];
k++;
}
factor.Add(r[i], k);
sort_exp.Add(k);
}
}
sort_exp.Sort();
Console.Write(" The Ordered Prime Signature of " +
t + " is : \n{ ");
for (int i = 0; i < sort_exp.Count; i++)
{
if (i != sort_exp.Count - 1)
Console.Write(sort_exp[i] + ", ");
else
Console.Write(sort_exp[i] + " }\n");
}
return sort_exp;
}
static void divisors(int n)
{
int f = 1, l;
List<int> div = signature(n);
l = div.Count;
for (int i = 0; i < l; i++)
{
div[i] += 1;
f *= div[i];
}
Console.Write("The total number of divisors of " +
n + " is " + f + "\n");
}
static void Main()
{
int n = 13;
divisors(n);
}
}
|
Javascript
<script>
function primes(n)
{
let prime = new Array(n+1).fill(true);
for (let i = 2; i * i <= n; i++)
{
if (prime[i] == true) {
for (let j = i * 2; j <= n; j += i)
prime[j] = false;
}
}
let arr = new Array();
for (let i = 2; i <= n; i++)
{
if (prime[i])
arr.push(i);
}
return arr;
}
function signature(n)
{
let r = primes(n);
let factor = new Map();
let sort_exp = new Array();
let k;
let t = n;
for (let i = 0; i < r.length; i++)
{
if (n % r[i] == 0) {
k = 0;
while (n % r[i] == 0) {
n = Math.floor(n / r[i]);
k = k + 1;
}
factor.set(r[i], k);
sort_exp.push(k);
}
}
sort_exp.sort();
document.write(" The Ordered Prime Signature of ", t, " is :\n");
document.write("{");
for (let i = 0; i < sort_exp.length; i++)
{
if (i != sort_exp.length - 1)
document.write(sort_exp[i],",");
else
document.write(sort_exp[i], " } \n");
}
return sort_exp;
}
function divisors(n)
{
let f = 1;
let l;
let div = signature(n);
l = div.length;
for (let i = 0; i < l; i++)
{
div[i] += 1;
f *= div[i];
}
document.write("The total number of divisors of ", n, " is ", f);
}
let n = 13;
divisors(n);
</script>
|
Output: The Ordered Prime Signature of 13 is :
{ 1 }
The total number of divisors of 13 is 2
Application :
Finding the ordered prime signature of a number has utilities in finding number of divisors. In fact, the total number of divisors of a number can be inferred from the ordered prime signature of that number. To accomplish this, just add one to each element present in the ordered prime signature and then multiply those elements. The product, thus obtained gives the total number of divisors of the number (including 1 and the number itself).
Share your thoughts in the comments
Please Login to comment...