Number of days after which tank will become empty

Given a tank with capacity C liters which is completely filled in starting. Everyday tank is filled with l liters of water and in the case of overflow extra water is thrown out. Now on i-th day i liters of water is taken out for drinking. We need to find out the day at which tank will become empty the first time.

Examples:

Input : Capacity = 5        
        l = 2
Output : 4
At the start of 1st day, water in tank = 5    
and at the end of the 1st day = (5 - 1) = 4
At the start of 2nd day, water in tank = 4 + 2 = 6
but tank capacity is 5 so water = 5
and at the end of the 2nd day = (5 - 2) = 3
At the start of 3rd day, water in tank = 3 + 2 = 5
and at the end of the 3rd day = (5 - 3) = 2
At the start of 4th day, water in tank = 2 + 2 = 4
and at the end of the 4th day = (4 - 4) = 0
    So final answer will be 4

We can see that tank will be full for starting (l + 1) days because water taken out is less than water being filled. After that, each day water in the tank will be decreased by 1 more liter and on (l + 1 + i)th day (C – (i)(i + 1) / 2) liter water will remain before taking drinking water. 

Now we need to find a minimal day (l + 1 + K), in which even after filling the tank by l liters we have water less than l in tank i.e. on (l + 1 + K – 1)th day tank becomes empty so our goal is to find minimum K such that, 
C – K(K + 1) / 2 <= l

We can solve above equation using binary search and then (l + K) will be our answer. Total time complexity of solution will be O(log C) 

C++

// C/C++ code to find number of days after which
// tank will become empty
#include <bits/stdc++.h>
using namespace std;

// Utility method to get sum of first n numbers
int getCumulateSum(int n)
{
    return (n * (n + 1)) / 2;
}

// Method returns minimum number of days after
// which tank will become empty
int minDaysToEmpty(int C, int l)
{
    // if water filling is more than capacity then
    // after C days only tank will become empty
    if (C <= l)
        return C;

    // initialize binary search variable
    int lo = 0;
    int hi = 1e4;
    int mid;

    // loop until low is less than high
    while (lo < hi) {
        mid = (lo + hi) / 2;

        // if cumulate sum is greater than (C - l)
        // then search on left side
        if (getCumulateSum(mid) >= (C - l))
            hi = mid;

        // if (C - l) is more then search on
        // right side
        else
            lo = mid + 1;
    }

    // final answer will be obtained by adding
    // l to binary search result
    return (l + lo);
}

// Driver code to test above methods
int main()
{
    int C = 5;
    int l = 2;

    cout << minDaysToEmpty(C, l) << endl;
    return 0;
}

Java

// Java code to find number of days after which
// tank will become empty
public class Tank_Empty {

    // Utility method to get sum of first n numbers
    static int getCumulateSum(int n)
    {
        return (n * (n + 1)) / 2;
    }

    // Method returns minimum number of days after
    // which tank will become empty
    static int minDaysToEmpty(int C, int l)
    {
        // if water filling is more than capacity then
        // after C days only tank will become empty
        if (C <= l)
            return C;

        // initialize binary search variable
        int lo = 0;
        int hi = (int)1e4;
        int mid;

        // loop until low is less than high
        while (lo < hi) {

            mid = (lo + hi) / 2;

            // if cumulate sum is greater than (C - l)
            // then search on left side
            if (getCumulateSum(mid) >= (C - l))
                hi = mid;

            // if (C - l) is more then search on
            // right side
            else
                lo = mid + 1;
        }

        // final answer will be obtained by adding
        // l to binary search result
        return (l + lo);
    }

    // Driver code to test above methods
    public static void main(String args[])
    {
        int C = 5;
        int l = 2;

        System.out.println(minDaysToEmpty(C, l));
    }
}
// This code is contributed by Sumit Ghosh

Python3

# Python3 code to find number of days
# after which tank will become empty

# Utility method to get
# sum of first n numbers
def getCumulateSum(n):

    return int((n * (n + 1)) / 2)


# Method returns minimum number of days
# after  which tank will become empty
def minDaysToEmpty(C, l):

    # if water filling is more than
    # capacity then after C days only
    # tank will become empty
    if (C <= l) : return C

    # initialize binary search variable
    lo, hi = 0, 1e4

    # loop until low is less than high
    while (lo < hi):
        mid = int((lo + hi) / 2)

        # if cumulate sum is greater than (C - l)
        # then search on left side
        if (getCumulateSum(mid) >= (C - l)):
            hi = mid

        # if (C - l) is more then
        # search on right side
        else:
            lo = mid + 1

    # Final answer will be obtained by
    # adding l to binary search result
    return (l + lo)

# Driver code
C, l = 5, 2
print(minDaysToEmpty(C, l))

# This code is contributed by Smitha Dinesh Semwal.

C#

// C# code to find number
// of days after which
// tank will become empty
using System;

class GFG
{

    // Utility method to get
    // sum of first n numbers
    static int getCumulateSum(int n)
    {
        return (n * (n + 1)) / 2;
    }

    // Method returns minimum
    // number of days after
    // which tank will become empty
    static int minDaysToEmpty(int C,
                              int l)
    {
        // if water filling is more
        // than capacity then after
        // C days only tank will
        // become empty
        if (C <= l)
            return C;

        // initialize binary
        // search variable
        int lo = 0;
        int hi = (int)1e4;
        int mid;

        // loop until low is
        // less than high
        while (lo < hi)
        {

            mid = (lo + hi) / 2;

            // if cumulate sum is
            // greater than (C - l)
            // then search on left side
            if (getCumulateSum(mid) >= (C - l))
                hi = mid;

            // if (C - l) is more then
            // search on right side
            else
                lo = mid + 1;
        }

        // final answer will be
        // obtained by adding
        // l to binary search result
        return (l + lo);
    }

    // Driver code
    static public void Main ()
    {
        int C = 5;
        int l = 2;

        Console.WriteLine(minDaysToEmpty(C, l));
    }
}

// This code is contributed by ajit

Javascript

<script>

// Javascript code to find number
// of days after which
// tank will become empty

// Utility method to get
// sum of first n numbers
function getCumulateSum(n)
{
    return parseInt((n * (n + 1)) / 2, 10);
}

// Method returns minimum
// number of days after
// which tank will become empty
function minDaysToEmpty(C, l)
{

    // If water filling is more
    // than capacity then after
    // C days only tank will
    // become empty
    if (C <= l)
        return C;

    // Initialize binary
    // search variable
    let lo = 0;
    let hi = 1e4;
    let mid;

    // Loop until low is
    // less than high
    while (lo < hi)
    {
        mid = parseInt((lo + hi) / 2, 10);

        // If cumulate sum is
        // greater than (C - l)
        // then search on left side
        if (getCumulateSum(mid) >= (C - l))
            hi = mid;

        // If (C - l) is more then
        // search on right side
        else
            lo = mid + 1;
    }

    // Final answer will be
    // obtained by adding
    // l to binary search result
    return (l + lo);
}

// Driver code
let C = 5;
let l = 2;

document.write(minDaysToEmpty(C, l));

// This code is contributed by rameshtravel07
</script>

Output:

4

Alternate Solution : 
It can be solved mathematically with a simple formula:

Let’s Assume C>L. Let d be the amount of days after the Lth when the tank become empty.During that time, there will be (d-1)refills and d withdrawals. 
Hence we need to solve this equation : 

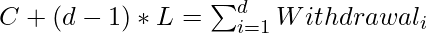
Sum of all withdrawals is a sum of arithmetic progression,therefore : 

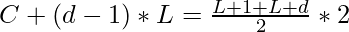
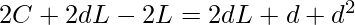
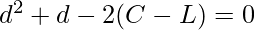
Discriminant = 1+8(C-L)>0,because C>L. 
Skipping the negative root, we get the following formula: 

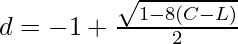
Therefore, the final answer is: 

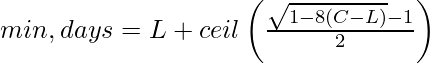
C++

// C/C++ code to find number of days after which
// tank will become empty
#include <bits/stdc++.h>
using namespace std;

// Method returns minimum number of days after
// which tank will become empty
int minDaysToEmpty(int C, int l)
{
    if (l >= C)
        return C;

    double eq_root = (std::sqrt(1+8*(C-l)) - 1) / 2;
    return std::ceil(eq_root) + l;
}

// Driver code to test above methods
int main()
{
    cout << minDaysToEmpty(5, 2) << endl;
    cout << minDaysToEmpty(6514683, 4965) << endl;
    return 0;
}

Java

// Java code to find number of days
// after which tank will become empty
import java.lang.*;
class GFG {

// Method returns minimum number of days
// after which tank will become empty
static int minDaysToEmpty(int C, int l)
{
    if (l >= C) return C;

    double eq_root = (Math.sqrt(1 + 8 *
                     (C - l)) - 1) / 2;
    return (int)(Math.ceil(eq_root) + l);
}

// Driver code
public static void main(String[] args)
{
    System.out.println(minDaysToEmpty(5, 2));
    System.out.println(minDaysToEmpty(6514683, 4965));
}
}

// This code is contributed by Smitha Dinesh Semwal.

Python3

# Python3 code to find number of days
# after which tank will become empty
import math

# Method returns minimum number of days
# after which tank will become empty
def minDaysToEmpty(C, l):

    if (l >= C): return C

    eq_root = (math.sqrt(1 + 8 * (C - l)) - 1) / 2
    return math.ceil(eq_root) + l

# Driver code
print(minDaysToEmpty(5, 2))
print(minDaysToEmpty(6514683, 4965))

# This code is contributed by Smitha Dinesh Semwal.

C#

// C# code to find number
// of days after which
// tank will become empty
using System;

class GFG
{

// Method returns minimum
// number of days after
// which tank will become empty
static int minDaysToEmpty(int C,
                          int l)
{
    if (l >= C) return C;

    double eq_root = (Math.Sqrt(1 + 8 *
                     (C - l)) - 1) / 2;
    return (int)(Math.Ceiling(eq_root) + l);
}

// Driver code
static public void Main ()
{
    Console.WriteLine(minDaysToEmpty(5, 2));
    Console.WriteLine(minDaysToEmpty(6514683,
                                     4965));
}
}

// This code is contributed by ajit

PHP

<?php
// PHP code to find number
// of days after which
// tank will become empty

// Method returns minimum
// number of days after
// which tank will become empty
function minDaysToEmpty($C, $l)
{
    if ($l >= $C)
        return $C;

    $eq_root = (int)sqrt(1 + 8 *
                   ($C - $l) - 1) / 2;
    return ceil($eq_root) + $l;
}

// Driver code
echo minDaysToEmpty(5, 2), "\n";
echo minDaysToEmpty(6514683,
                    4965), "\n";

// This code is contributed
// by akt_mit
?>

Javascript

<script>

// Javascript code to find number
// of days after which
// tank will become empty

// Method returns minimum
// number of days after
// which tank will become empty
function minDaysToEmpty(C, l)
{
    if (l >= C) return C;

    let eq_root = (Math.sqrt(1 + 8 *
                            (C - l)) - 1) / 2;
    return (Math.ceil(eq_root) + l);
}

// Driver code
document.write(minDaysToEmpty(5, 2) + "</br>");
document.write(minDaysToEmpty(6514683, 4965));

// This code is contributed by suresh07

</script>

Output :

4
8573

Thanks to Andrey Khayrutdinov for suggesting this solution.
If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.