Next smallest prime palindrome
Last Updated :
19 Jul, 2022
Given a positive integer N where 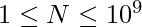 . The task is to find the smallest prime palindrome greater than or equal to N.
. The task is to find the smallest prime palindrome greater than or equal to N.
Examples:
Input: 8
Output: 11
Input: 7000000000
Output: 10000500001
Approach:
The Naive approach is to loop from N + 1 until we found the next smallest prime palindrome greater than or equal to N.
Efficient Approach:
Let’s say P = R is a the next smallest prime-palindrome greater than or equal to N.
Now since R is a palindrome, the first half of the digits of R can be used to determine R up to two possibilities. Let k be the first half of the digits in R. For eg. if k = 123, then R = 12321 or R = 123321.
Thus, we iterate through each k upto 105 and create the associated palindrome R, and check whether R is a prime or not.
Also, we will handle the odd and even palindromes separately, and break them when we found our result.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
bool isPrime(ll n)
{
if (n < 2) return false;
for (ll i = 2; i <= sqrt(n); i++)
{
if (n % i == 0) return false;
}
return true;
}
ll nextPrimePalindrome(ll N)
{
for (ll k = 1; k < 1000000; k++)
{
string s = to_string(k);
string z(s.begin(), s.end());
reverse(z.begin(), z.end());
ll x = stoll(s + z.substr(1));
if (x >= N and isPrime(x)) return x;
s = to_string(k);
z = string(s.begin(), s.end());
reverse(z.begin(), z.end());
x = stoll(s + z);
if (x >= N and isPrime(x)) return x;
}
}
int main()
{
ll N = 7000000000;
cout << nextPrimePalindrome(N) << endl;
return 0;
}
|
Java
class GFG
{
static boolean isPrime(long n)
{
if (n < 2) return false;
for (long i = 2; i <= Math.sqrt(n); i++)
{
if (n % i == 0) return false;
}
return true;
}
static String reverse(String s)
{
String s1 = "";
for(int i = s.length() - 1; i >= 0; i--)
s1 += s.charAt(i);
return s1;
}
static long nextPrimePalindrome(long N)
{
for (long k = 1; k < 1000000l; k++)
{
String s = ""+k;
String z;
z = reverse(s);
long x = Long.parseLong(s + z.substring(1, z.length()));
if (x >= N && isPrime(x))
return x;
s = ""+(k);
z = s;
z = reverse(z);
x = Long.parseLong(s + z);
if (x >= N && isPrime(x)) return x;
}
return -1;
}
public static void main(String args[])
{
long N = 7000000000l;
System.out.println( nextPrimePalindrome(N) );
}
}
|
Python3
import math
def is_prime(n):
return n > 1 and all(n % d for d in range(2, int(math.sqrt(n)) + 1))
def NextprimePalindrome(N):
for k in range(1, 10**6):
s = str(k)
x = int(s + s[-2::-1])
if x >= N and is_prime(x):
return x
s = str(k)
x = int(s + s[-1::-1])
if x >= N and is_prime(x):
return x
N = 7000000000
print(NextprimePalindrome(N))
|
C#
using System;
class GFG
{
static bool isPrime(long n)
{
if (n < 2) return false;
for (long i = 2; i <= Math.Sqrt(n); i++)
{
if (n % i == 0) return false;
}
return true;
}
static String reverse(String s)
{
String s1 = "";
for(int i = s.Length - 1; i >= 0; i--)
s1 += s[i];
return s1;
}
static long nextPrimePalindrome(long N)
{
for (long k = 1; k < 1000000; k++)
{
String s = ""+k;
String z;
z = reverse(s);
long x = long.Parse(s + z.Substring(1, z.Length - 1));
if (x >= N && isPrime(x))
return x;
s = ""+(k);
z = s;
z = reverse(z);
x = long.Parse(s + z);
if (x >= N && isPrime(x)) return x;
}
return -1;
}
public static void Main(String []args)
{
long N = 7000000000;
Console.WriteLine( nextPrimePalindrome(N) );
}
}
|
Javascript
<script>
function isPrime( n)
{
if (n < 2) return false;
for (var i = 2; i <= Math.sqrt(n); i++)
{
if (n % i == 0) return false;
}
return true;
}
function reverse( s)
{
var s1 = "";
for(var i = s.length - 1; i >= 0; i--)
s1 += s[i];
return s1;
}
function nextPrimePalindrome( N)
{
for (var k = 1; k < 1000000; k++)
{
var s = ""+k;
var z;
z=reverse(s);
var x = Number(s + z.substring(1,z.length));
if (x >= N && isPrime(x)) return x;
s = ""+k;
z = s;
z=reverse(z);
x = Number(s + z);
if (x >= N && isPrime(x)) return x;
}
}
var N = 7000000000;
document.write(nextPrimePalindrome(N) + "<br>");
</script>
|
Time Complexity: O(N*sqrt(N)) where N is upper limit and the sqrt(N) term comes from checking if a candidate is prime.
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...