Modulus of all pairwise consecutive elements in an Array
Last Updated :
09 Sep, 2022
Given an array of 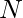 elements. The task is to print the modulus of all of the pairwise consecutive elements. That is for all pair of consecutive elements say ((a[i], a[i+1])), print (a[i] % a[i+1]).
elements. The task is to print the modulus of all of the pairwise consecutive elements. That is for all pair of consecutive elements say ((a[i], a[i+1])), print (a[i] % a[i+1]).
Note: Consecutive pairs of an array of size N are (a[i], a[i+1]) for all i ranging from 0 to N-2.
Examples:
Input: arr[] = {8, 5, 4, 3, 15, 20}
Output: 3 1 1 3 15
Input: arr[] = {5, 10, 15, 20}
Output: 5 10 15
Approach: The solution is to traverse the array and calculate and print the modulus of every pair (arr[i], arr[i+1]).
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
void pairwiseModulus(int arr[], int n)
{
for (int i = 0; i < n - 1; i++) {
cout << (arr[i] % arr[i + 1]) << " ";
}
}
int main()
{
int arr[] = { 8, 5, 4, 3, 15, 20 };
int n = sizeof(arr) / sizeof(arr[0]);
pairwiseModulus(arr, n);
return 0;
}
|
C
#include <stdio.h>
void pairwiseModulus(int arr[], int n)
{
for (int i = 0; i < n - 1; i++) {
printf("%d ",arr[i] % arr[i + 1]);
}
}
int main()
{
int arr[] = { 8, 5, 4, 3, 15, 20 };
int n = sizeof(arr) / sizeof(arr[0]);
pairwiseModulus(arr, n);
return 0;
}
|
Java
import java.util.*;
class Geeks {
static void pairwiseModulus(int arr[], int n)
{
for (int i = 0; i < n - 1; i++) {
System.out.println((arr[i] % arr[i + 1]));
}
}
public static void main(String args[])
{
int arr[] = { 8, 5, 4, 3, 15, 20 };
int n = arr.length;
pairwiseModulus(arr, n);
}
}
|
Python3
def pairwiseModulus(arr, n):
for i in range(0, n - 1, 1):
print((arr[i] % arr[i + 1]),
end = " ")
if __name__ == '__main__':
arr = [8, 5, 4, 3, 15, 20]
n = len(arr)
pairwiseModulus(arr, n)
|
C#
using System;
class Geeks {
static void pairwiseModulus(int[] arr, int n)
{
for (int i = 0; i < n - 1; i++) {
Console.WriteLine((arr[i] % arr[i + 1]));
}
}
public static void Main(String []args)
{
int[] arr = {8, 5, 4, 3, 15, 20};
int n = arr.Length;
pairwiseModulus(arr, n);
}
}
|
PHP
<?php
function pairwiseModulus( $arr, $n)
{
for ($i = 0; $i < $n - 1; $i++) {
echo ($arr[$i] % $arr[$i + 1]), " ";
}
}
$arr = array( 8, 5, 4, 3, 15, 20 );
$n = sizeof($arr) / sizeof($arr[0]);
pairwiseModulus($arr, $n);
?>
|
Javascript
<script>
function pairwiseModulus(arr , n) {
for (i = 0; i < n - 1; i++) {
document.write((arr[i] % arr[i + 1]) + " ");
}
}
var arr = [ 8, 5, 4, 3, 15, 20 ];
var n = arr.length;
pairwiseModulus(arr, n);
</script>
|
Complexity Analysis:
- Time complexity: O(n)
- Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...