ML | Fuzzy Clustering
Last Updated :
01 Nov, 2023
Prerequisite: Clustering in Machine Learning
Clustering is an unsupervised machine learning technique that divides the given data into different clusters based on their distances (similarity) from each other.
The unsupervised k-means clustering algorithm gives the values of any point lying in some particular cluster to be either as 0 or 1 i.e., either true or false. But the fuzzy logic gives the fuzzy values of any particular data point to be lying in either of the clusters. Here, in fuzzy c-means clustering, we find out the centroid of the data points and then calculate the distance of each data point from the given centroids until the clusters formed become constant.
Suppose the given data points are {(1, 3), (2, 5), (6, 8), (7, 9)}
Fuzzy Clustering is a type of clustering algorithm in machine learning that allows a data point to belong to more than one cluster with different degrees of membership. Unlike traditional clustering algorithms, such as k-means or hierarchical clustering, which assign each data point to a single cluster, fuzzy clustering assigns a membership degree between 0 and 1 for each data point for each cluster.
Applications in several fields of Fuzzy clustering :
- Image segmentation: Fuzzy clustering can be used to segment images by grouping pixels with similar properties together, such as color or texture.
- Pattern recognition: Fuzzy clustering can be used to identify patterns in large datasets by grouping similar data points together.
- Marketing: Fuzzy clustering can be used to segment customers based on their preferences and purchasing behavior, allowing for more targeted marketing campaigns.
- Medical diagnosis: Fuzzy clustering can be used to diagnose diseases by grouping patients with similar symptoms together.
- Environmental monitoring: Fuzzy clustering can be used to identify areas of environmental concern by grouping together areas with similar pollution levels or other environmental indicators.
- Traffic flow analysis: Fuzzy clustering can be used to analyze traffic flow patterns by grouping similar traffic patterns together, allowing for better traffic management and planning.
- Risk assessment: Fuzzy clustering can be used to identify and quantify risks in various fields, such as finance, insurance, and engineering.
Advantages of Fuzzy Clustering:
- Flexibility: Fuzzy clustering allows for overlapping clusters, which can be useful when the data has a complex structure or when there are ambiguous or overlapping class boundaries.
- Robustness: Fuzzy clustering can be more robust to outliers and noise in the data, as it allows for a more gradual transition from one cluster to another.
- Interpretability: Fuzzy clustering provides a more nuanced understanding of the structure of the data, as it allows for a more detailed representation of the relationships between data points and clusters.
Disadvantages of Fuzzy Clustering:
- Complexity: Fuzzy clustering algorithms can be computationally more expensive than traditional clustering algorithms, as they require optimization over multiple membership degrees.
- Model selection: Choosing the right number of clusters and membership functions can be challenging, and may require expert knowledge or trial and error.
- If you’re interested in learning more about fuzzy clustering, you might consider reading “Fuzzy Clustering and Its Applications” by James C. Bezdek or “An Introduction to Fuzzy Clustering” by Witold Pedrycz and Fernando Gomide.
The steps to perform the algorithm are:
Step 1: Initialize the data points into the desired number of clusters randomly.
Let us assume there are 2 clusters in which the data is to be divided, initializing the data point randomly. Each data point lies in both clusters with some membership value which can be assumed anything in the initial state.
The table below represents the values of the data points along with their membership (gamma) in each cluster.
Cluster (1, 3) (2, 5) (4, 8) (7, 9)
1) 0.8 0.7 0.2 0.1
2) 0.2 0.3 0.8 0.9
Step 2: Find out the centroid.
The formula for finding out the centroid (V) is:
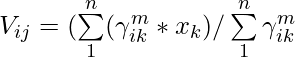
Where, µ is fuzzy membership value of the data point, m is the fuzziness parameter (generally taken as 2), and xk is the data point.
Here,
V11 = (0.8^2 *1 + 0.7^2 * 2 + 0.2^2 * 4 + 0.1^2 * 7) / ( (0.8^2 + 0.7^2 + 0.2^2 + 0.1^2 ) = 1.568
V12 = (0.8^2 *3 + 0.7^2 * 5 + 0.2^2 * 8 + 0.1^2 * 9) / ( (0.8^2 + 0.7^2 + 0.2^2 + 0.1^2 ) = 4.051
V21 = (0.2^2 *1 + 0.3^2 * 2 + 0.8^2 * 4 + 0.9^2 * 7) / ( (0.2^2 + 0.3^2 + 0.8^2 + 0.9^2 ) = 5.35
V22 = (0.2^2 *3 + 0.3^2 * 5 + 0.8^2 * 8 + 0.9^2 * 9) / ( (0.2^2 + 0.3^2 + 0.8^2 + 0.9^2 ) = 8.215
Centroids are: (1.568, 4.051) and (5.35, 8.215)
Step 3: Find out the distance of each point from the centroid.
D11 = ((1 - 1.568)2 + (3 - 4.051)2)0.5 = 1.2
D12 = ((1 - 5.35)2 + (3 - 8.215)2)0.5 = 6.79
Similarly, the distance of all other points is computed from both the centroids.
Step 4: Updating membership values.
![Rendered by QuickLaTeX.com \gamma = \sum \limits_1^n {(d_{ki}^2 /d_{kj}^2)}^{1/m-1} ]^{-1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d5005fe3b9a4b30eb231487bd0e1b9f8_l3.png)
For point 1 new membership values are:
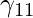 = [{ [(1.2)2 / (1.2)2] + [(1.2)2 / (6.79)2]} ^ {(1 / (2 – 1))} ] -1 = 0.96
= [{ [(1.2)2 / (1.2)2] + [(1.2)2 / (6.79)2]} ^ {(1 / (2 – 1))} ] -1 = 0.96
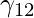 = [{ [(6.79)2 / (6.79)2] + [(6.79)2 / (1.2)2]} ^ {(1 / (2 – 1))} ] -1 = 0.04
= [{ [(6.79)2 / (6.79)2] + [(6.79)2 / (1.2)2]} ^ {(1 / (2 – 1))} ] -1 = 0.04
Alternatively,
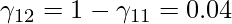
Similarly, compute all other membership values, and update the matrix.
Step 5: Repeat the steps(2-4) until the constant values are obtained for the membership values or the difference is less than the tolerance value (a small value up to which the difference in values of two consequent updations is accepted).
Step 6: Defuzzify the obtained membership values.
Implementation: The fuzzy scikit learn library has a pre-defined function for fuzzy c-means which can be used in Python. For using fuzzy c-means you need to install the skfuzzy library.
pip install sklearn
pip install skfuzzy
Example :
Python3
import numpy as np
import skfuzzy as fuzz
from skfuzzy import control as ctrl
np.random.seed(0)
data = np.random.rand(100, 2)
n_clusters = 3
cntr, u, u0, d, jm, p, fpc = fuzz.cluster.cmeans(
data.T, n_clusters, 2, error=0.005, maxiter=1000, init=None
)
cluster_membership = np.argmax(u, axis=0)
print('Cluster Centers:', cntr)
print('Cluster Membership:', cluster_membership)
|
output:
Cluster Centers: [[0.42363557 0.68304616]
[0.52768166 0.38180987]
[0.39967863 0.31042639]]
Cluster Membership: [1 0 1 2 1 0 0 2 0 2 1 0 0 0 1 2 1 1 0 2 1 0 0 2 1 1 2 0 1 0 0 2 0 2 1 1 0
1 0 2 0 0 2 0 0 1 1 1 1 2 2 0 1 1 0 1 0 0 2 2 2 0 1 1 2 0 0 0 2 1 0 1 0 0
1 2 0 0 2 2 1 1 0 2 1 0 2 2 1 1 0 2 1 0 2 1 0 2 2 2 0 1 0 2]
Share your thoughts in the comments
Please Login to comment...