Minimum number of Parentheses to be added to make it valid
Last Updated :
09 May, 2023
Given a string S of parentheses ‘(‘ or ‘)’ where, 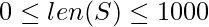 . The task is to find a minimum number of parentheses ‘(‘ or ‘)’ (at any positions) we must add to make the resulting parentheses string is valid.
. The task is to find a minimum number of parentheses ‘(‘ or ‘)’ (at any positions) we must add to make the resulting parentheses string is valid.
Examples:
Input: str = "())"
Output: 1
One '(' is required at beginning.
Input: str = "((("
Output: 3
Three ')' is required at end.Approach 1: Iterative Approach
We keep the track of balance of the string i:e the number of ‘(‘ minus the number of ‘)’. A string is valid if its balance is 0, and also every prefix has non-negative balance.
Now, consider the balance of every prefix of S. If it is ever negative (say, -1), we must add a ‘(‘ bracket at the beginning. Also, if the balance of S is positive (say, +P), we must add P times ‘)’ brackets at the end.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minParentheses(string p)
{
int bal = 0;
int ans = 0;
for (int i = 0; i < p.length(); ++i) {
bal += p[i] == '(' ? 1 : -1;
if (bal == -1) {
ans += 1;
bal += 1;
}
}
return bal + ans;
}
int main()
{
string p = "())";
cout << minParentheses(p);
return 0;
}
|
Java
public class GFG {
static int minParentheses(String p)
{
int bal = 0;
int ans = 0;
for (int i = 0; i < p.length(); ++i) {
bal += p.charAt(i) == '(' ? 1 : -1;
if (bal == -1) {
ans += 1;
bal += 1;
}
}
return bal + ans;
}
public static void main(String args[])
{
String p = "())";
System.out.println(minParentheses(p));
}
}
|
Python3
def minParentheses(p):
bal=0
ans=0
for i in range(0,len(p)):
if(p[i]=='('):
bal+=1
else:
bal+=-1
if(bal==-1):
ans+=1
bal+=1
return bal+ans
if __name__=='__main__':
p = "())"
print(minParentheses(p))
|
C#
using System;
class GFG
{
static int minParentheses(string p)
{
int bal = 0;
int ans = 0;
for (int i = 0; i < p.Length; ++i)
{
bal += p[i] == '(' ? 1 : -1;
if (bal == -1)
{
ans += 1;
bal += 1;
}
}
return bal + ans;
}
public static void Main()
{
string p = "())";
Console.WriteLine(minParentheses(p));
}
}
|
PHP
<?php
function minParentheses($p)
{
$bal = 0;
$ans = 0;
for ($i = 0; $i < strlen($p); ++$i)
{
if ($p[$i] == '(' )
$bal += 1 ;
else
$bal += -1;
if ($bal == -1)
{
$ans += 1;
$bal += 1;
}
}
return $bal + $ans;
}
$p = "())";
echo minParentheses($p);
?>
|
Javascript
<script>
function minParentheses( p)
{
var bal = 0;
var ans = 0;
for (var i = 0; i < p.length; ++i) {
bal += p[i] == '(' ? 1 : -1;
if (bal == -1) {
ans += 1;
bal += 1;
}
}
return bal + ans;
}
var p = "())";
document.write( minParentheses(p));
</script>
|
Complexity Analysis:
- Time Complexity: O(N), where N is the length of S.
- Space Complexity: O(1).
Approach 2: Using Stack
We can also solve this problem using a stack data structure.
- We push the index of every ‘(‘ character onto the stack, and whenever we encounter a ‘)’ character, we pop the top index from the stack.
- This indicates that the corresponding ‘(‘ has been paired with the current ‘)’.
- If at any point the stack is empty and we encounter a ‘)’ character, it means we need to add a ‘(‘ character to the beginning of the string to make it valid.
- Similarly, if after processing the entire string there are still indices left in the stack, it means we need to add ‘)’ characters to the end of the string to make it valid.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minParentheses(string p)
{
stack<int> stk;
int ans = 0;
for (int i = 0; i < p.length(); ++i) {
if (p[i] == '(') {
stk.push(i);
}
else {
if (!stk.empty()) {
stk.pop();
}
else {
ans += 1;
}
}
}
ans += stk.size();
return ans;
}
int main()
{
string p = "())";
cout << minParentheses(p);
return 0;
}
|
Java
import java.util.Stack;
public class Main {
public static int minParentheses(String p) {
Stack<Integer> stk = new Stack<>();
int ans = 0;
for (int i = 0; i < p.length(); ++i) {
if (p.charAt(i) == '(') {
stk.push(i);
} else {
if (!stk.empty()) {
stk.pop();
} else {
ans += 1;
}
}
}
ans += stk.size();
return ans;
}
public static void main(String[] args) {
String p = "())";
System.out.println(minParentheses(p));
}
}
|
Python3
def minParentheses(p):
stk = []
ans = 0
for i in range(len(p)):
if p[i] == '(':
stk.append(i)
else:
if len(stk) > 0:
stk.pop()
else:
ans += 1
ans += len(stk)
return ans
p = "())"
print(minParentheses(p))
|
C#
using System;
using System.Collections.Generic;
public class Program {
public static int MinParentheses(string p) {
Stack<int> stk = new Stack<int>();
int ans = 0;
for (int i = 0; i < p.Length; ++i) {
if (p[i] == '(') {
stk.Push(i);
} else {
if (stk.Count > 0) {
stk.Pop();
} else {
ans += 1;
}
}
}
ans += stk.Count;
return ans;
}
public static void Main() {
string p = "())";
Console.WriteLine(MinParentheses(p));
}
}
|
Javascript
function minParentheses(p) {
let stk = [];
let ans = 0;
for (let i = 0; i < p.length; i++) {
if (p[i] === '(') {
stk.push(i);
} else {
if (stk.length > 0) {
stk.pop();
} else {
ans += 1;
}
}
}
ans += stk.length;
return ans;
}
let p = "())";
console.log(minParentheses(p));
|
Time Complexity: O(n), where n is the length of the input string.
Space Complexity: O(n)
Approach 3: Using string manipulation
- Continuously search for the substring “()” in the input string.
- If the substring “()” is found, replace it with an empty string.
- Repeat steps 1 and 2 until the substring “()” can no longer be found.
- The length of the resulting string is the minimum number of parentheses needed to make the string valid.
Here is the implementation of above approach:
C++
#include <iostream>
#include <string>
using namespace std;
int minParentheses(string s) {
while (s.find("()") != -1) {
s.replace(s.find("()"), 2, "");
}
return s.length();
}
int main() {
string s = "(((";
cout << minParentheses(s) << endl;
return 0;
}
|
Java
public class Solution {
public static int minParentheses(String s) {
while (s.indexOf("()") != -1) {
s = s.replace("()", "");
}
return s.length();
}
public static void main(String[] args) {
String s = "(((";
System.out.println(minParentheses(s));
}
}
|
Python3
def minParentheses(s: str) -> int:
while s.find("()") != -1:
s = s.replace("()", "")
return len(s)
s = "((("
print(minParentheses(s))
|
C#
using System;
public class Program {
public static void Main() {
string s = "(((";
Console.WriteLine(minParentheses(s));
}
public static int minParentheses(string s) {
while (s.IndexOf("()") != -1) {
s = s.Replace("()", "");
}
return s.Length;
}
}
|
Javascript
function minParentheses(s) {
while(s.indexOf("()") != -1) {
s = s.replace("()", "");
}
return s.length;
}
let s = "(((";
console.log(minParentheses(s));
|
Time Complexity: O(n^2) where n is the length of the input string. This is because the find() and replace() operations are called repeatedly in a loop.
Auxiliary Space: O(n) where n is the length of the input string. This is because the string s is being replaced in place and no additional data structures are being used.
Share your thoughts in the comments
Please Login to comment...