C++ Program To Check For Balanced Brackets In An Expression (Well-Formedness) Using Stack

Given an expression string exp, write a program to examine whether the pairs and the orders of “{“, “}”, “(“, “)”, “[“, “]” are correct in exp.

Example: 

Input: exp = “[()]{}{[()()]()}” 
Output: Balanced

Input: exp = “[(])” 
Output: Not Balanced 

Algorithm:

• Declare a character stack S.
• Now traverse the expression string exp. 
  1. If the current character is a starting bracket (‘(‘ or ‘{‘ or ‘[‘) then push it to stack.
  2. If the current character is a closing bracket (‘)’ or ‘}’ or ‘]’) then pop from stack and if the popped character is the matching starting bracket then fine else brackets are not balanced.
• After complete traversal, if there is some starting bracket left in stack then “not balanced”

Below image is a dry run of the above approach:

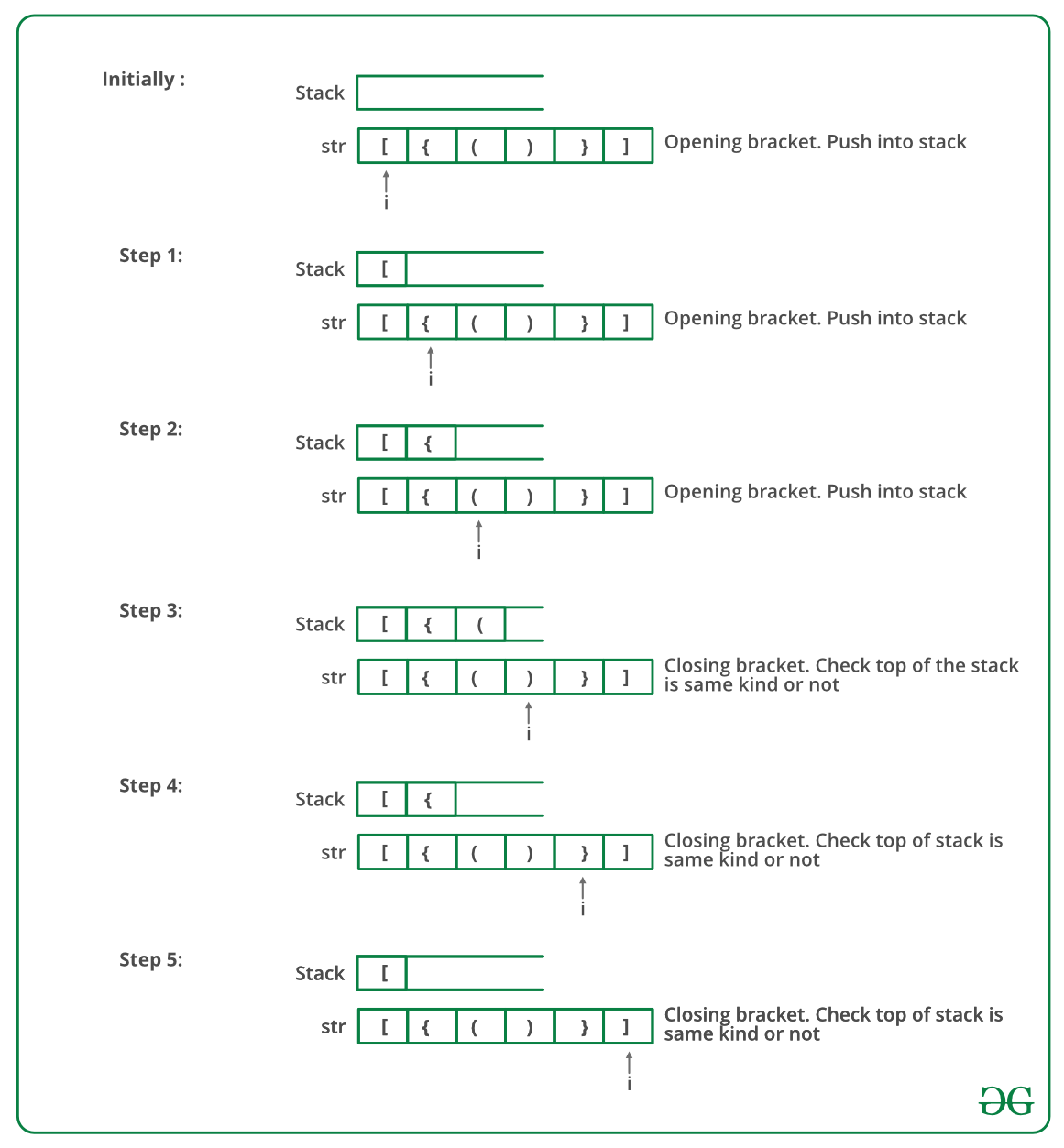
Below is the implementation of the above approach:

C++

// CPP program to check for balanced brackets.
#include <bits/stdc++.h>
using namespace std;

// function to check if brackets are balanced
bool areBracketsBalanced(string expr)
{
    stack<char> s;
    char x;

    // Traversing the Expression
    for (int i = 0; i < expr.length(); i++)
    {
        if (expr[i] == '(' || expr[i] == '['
            || expr[i] == '{')
        {
            // Push the element in the stack
            s.push(expr[i]);
            continue;
        }

        // IF current current character is not opening
        // bracket, then it must be closing. So stack
        // cannot be empty at this point.
        if (s.empty())
            return false;

        switch (expr[i]) {
        case ')':

            // Store the top element in a
            x = s.top();
            s.pop();
            if (x == '{' || x == '[')
                return false;
            break;

        case '}':

            // Store the top element in b
            x = s.top();
            s.pop();
            if (x == '(' || x == '[')
                return false;
            break;

        case ']':

            // Store the top element in c
            x = s.top();
            s.pop();
            if (x == '(' || x == '{')
                return false;
            break;
        }
    }

    // Check Empty Stack
    return (s.empty());
}

// Driver code
int main()
{
    string expr = "{()}[]";

    // Function call
    if (areBracketsBalanced(expr))
        cout << "Balanced";
    else
        cout << "Not Balanced";
    return 0;
}

Output

Balanced

Time Complexity: O(n) 
Auxiliary Space: O(n) for stack. 

Please refer complete article on Check for Balanced Brackets in an expression (well-formedness) using Stack for more details!