Minimum colors required such that edges forming cycle do not have same color
Last Updated :
31 May, 2021
Given a directed graph with V vertices and E edges without self-loops and multiple edges, the task is to find the minimum number of colors required such that edges of the same color do not form cycle and also find the colors for every edge.
Examples:
Input: V = {1, 2, 3}, E = {(1, 2), (2, 3), (3, 1)}
Output: 2
1 1 2
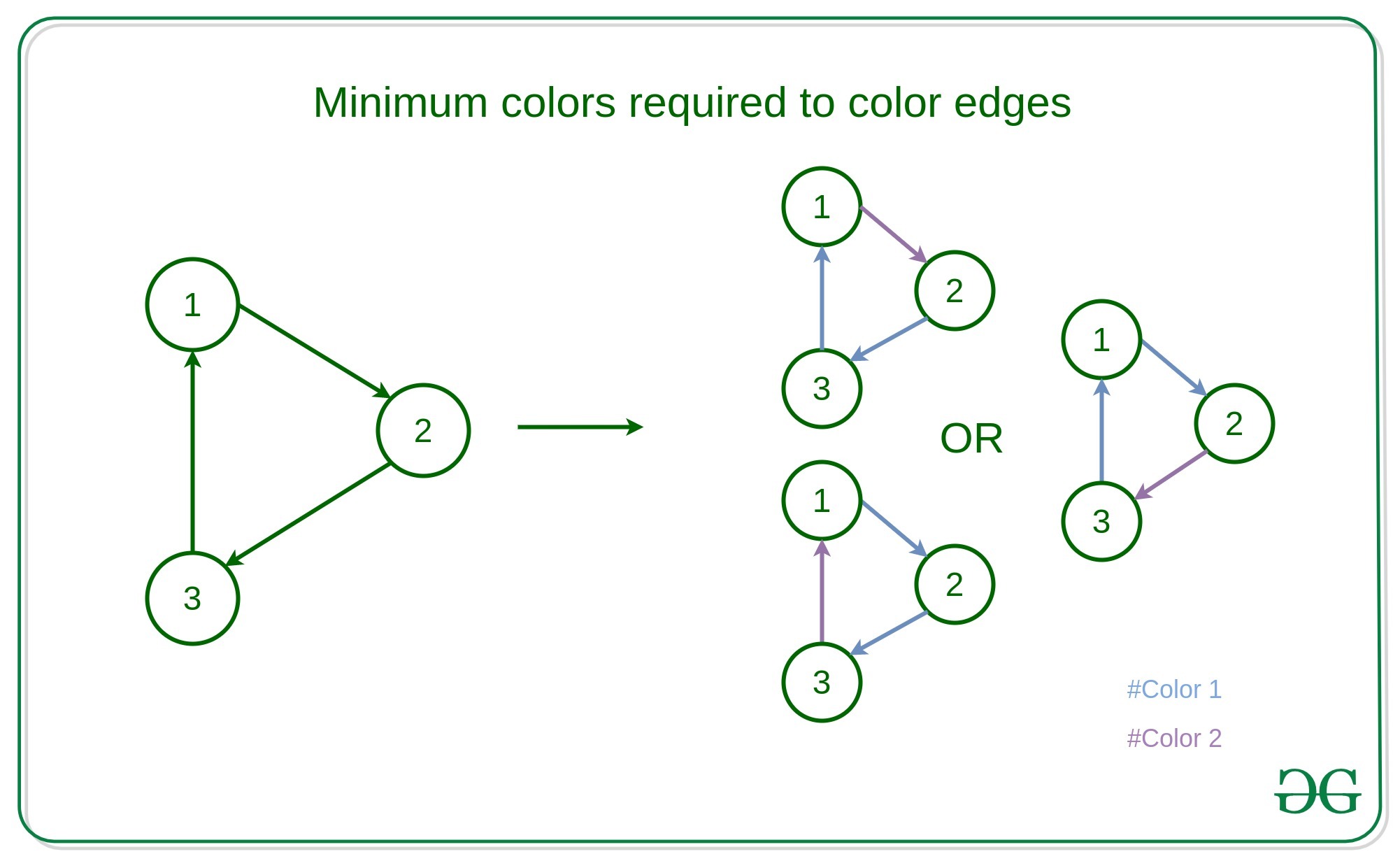
Explanation:
In the above given graph it forms only one cycle,
that is Vertices connecting 1, 2, 3 forms a cycle
Then the edges connecting 1->2 or 2->3 or 3->1 can be colored
with a different color such that edges forming cycle don’t have same color
Input: V = {1, 2, 3, 4, 5}, E = {(1, 2), (1, 3), (2, 3), (2, 4), (3, 4), (4, 5), (5, 3)}
Output: 2
Colors of Edges – 1 1 1 1 1 1 2
Explanation:
In the above given graph it forms only one cycle,
that is Vertices connecting 3, 4, 5 forms a cycle
Then the edges connecting 5->3 or 4->5 or 3->4 can be colored
with a different color such that edges forming cycle don’t have same color
Final Colors of the Edges –
{1: 1, 2: 1, 3: 1, 4: 1, 5: 1, 6: 1, 7: 2}
The above array denotes the pairs as – Edge : Color Code
Approach: The idea is to find the cycle in the graph, which can be done with the help of DFS for the Graph in which when a node which is already visited is visited again with a new edge, then that edges is colored with another color else if there is no cycle then all edges can be colored with only one color.
Algorithm:
- Mark every edges with color 1 and every vertices as unvisited.
- Traverse the graph using the DFS Traversal for the graph and mark the nodes visited.
- When a node which is visited already, then the edge connecting the vertex is marked to be colored with color 2.
- Print the colors of the edges when all the vertices are visited.
Explanation with Example:
Detailed Dry-run of the Example 1
| Current Vertex |
Current Edge |
Visited Vertices |
Colors of Edges |
Comments |
| 1 |
1–>2 |
{1} |
{1: 1, 2: 1, 3: 1} |
Node 1 is marked as visited and Calling DFS for node 2 |
| 2 |
2–>3 |
{1, 2} |
{1: 1, 2: 1, 3: 1} |
Node 2 is marked as visited and Calling DFS for node 3 |
| 3 |
3–>1 |
{1, 2} |
{1: 1, 2: 1, 3: 2} |
As 1 is already Visited color of Edge 3 is changed to 2 |
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
const int n = 5, m = 7;
vector<pair<int, int> > g[m];
int col[n];
bool cyc;
int res[m];
void dfs(int v)
{
col[v] = 1;
for (auto p : g[v]) {
int to = p.first, id = p.second;
if (col[to] == 0)
{
dfs(to);
res[id] = 1;
}
else if (col[to] == 2)
{
res[id] = 1;
}
else {
res[id] = 2;
cyc = true;
}
}
col[v] = 2;
}
int main()
{
g[0].push_back(make_pair(1, 0));
g[0].push_back(make_pair(2, 1));
g[1].push_back(make_pair(2, 2));
g[1].push_back(make_pair(3, 3));
g[2].push_back(make_pair(3, 4));
g[3].push_back(make_pair(4, 5));
g[4].push_back(make_pair(2, 6));
for (int i = 0; i < n; ++i) {
if (col[i] == 0)
{
dfs(i);
}
}
cout << (cyc ? 2 : 1) << endl;
for (int i = 0; i < m; ++i) {
cout << res[i] << ' ';
}
return 0;
}
|
Java
import java.util.*;
class GFG{
static int n = 5, m = 7;
static class pair
{
int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
static Vector<pair > []g = new Vector[m];
static int []col = new int[n];
static boolean cyc;
static int []res = new int[m];
static void dfs(int v)
{
col[v] = 1;
for (pair p : g[v]) {
int to = p.first, id = p.second;
if (col[to] == 0)
{
dfs(to);
res[id] = 1;
}
else if (col[to] == 2)
{
res[id] = 1;
}
else {
res[id] = 2;
cyc = true;
}
}
col[v] = 2;
}
public static void main(String[] args)
{
for(int i= 0; i < m; i++)
g[i] = new Vector<pair>();
g[0].add(new pair(1, 0));
g[0].add(new pair(2, 1));
g[1].add(new pair(2, 2));
g[1].add(new pair(3, 3));
g[2].add(new pair(3, 4));
g[3].add(new pair(4, 5));
g[4].add(new pair(2, 6));
for (int i = 0; i < n; ++i) {
if (col[i] == 0)
{
dfs(i);
}
}
System.out.print((cyc ? 2 : 1) +"\n");
for (int i = 0; i < m; ++i) {
System.out.print(res[i] +" ");
}
}
}
|
Python3
n = 5
m = 7;
g = [[] for i in range(m)]
col = [0 for i in range(n)];
cyc = True
res = [0 for i in range(m)];
def dfs(v):
col[v] = 1;
for p in g[v]:
to = p[0]
id = p[1];
if (col[to] == 0):
dfs(to);
res[id] = 1;
elif (col[to] == 2):
res[id] = 1;
else:
res[id] = 2;
cyc = True;
col[v] = 2;
if __name__=='__main__':
g[0].append([1, 0]);
g[0].append([2, 1]);
g[1].append([2, 2]);
g[1].append([3, 3]);
g[2].append([3, 4]);
g[3].append([4, 5]);
g[4].append([2, 6]);
for i in range(n):
if (col[i] == 0):
dfs(i);
print(2 if cyc else 1)
for i in range(m):
print(res[i], end=' ')
|
C#
using System;
using System.Collections.Generic;
class GFG{
static int n = 5, m = 7;
class pair
{
public int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
static List<pair> []g = new List<pair>[m];
static int []col = new int[n];
static bool cyc;
static int []res = new int[m];
static void dfs(int v)
{
col[v] = 1;
foreach (pair p in g[v]) {
int to = p.first, id = p.second;
if (col[to] == 0)
{
dfs(to);
res[id] = 1;
}
else if (col[to] == 2)
{
res[id] = 1;
}
else {
res[id] = 2;
cyc = true;
}
}
col[v] = 2;
}
public static void Main(String[] args)
{
for(int i= 0; i < m; i++)
g[i] = new List<pair>();
g[0].Add(new pair(1, 0));
g[0].Add(new pair(2, 1));
g[1].Add(new pair(2, 2));
g[1].Add(new pair(3, 3));
g[2].Add(new pair(3, 4));
g[3].Add(new pair(4, 5));
g[4].Add(new pair(2, 6));
for (int i = 0; i < n; ++i) {
if (col[i] == 0)
{
dfs(i);
}
}
Console.Write((cyc ? 2 : 1) +"\n");
for (int i = 0; i < m; ++i) {
Console.Write(res[i] +" ");
}
}
}
|
Javascript
<script>
const n = 5, m = 7;
let g = new Array();
for(let i = 0; i<m; i++){
g.push([])
}
let col = new Array(n).fill(0);
let cyc;
let res = new Array(m);
function dfs(v)
{
col[v] = 1;
for (let p of g[v]) {
let to = p[0]
let id = p[1];
if (col[to] == 0)
{
dfs(to);
res[id] = 1;
}
else if (col[to] == 2)
{
res[id] = 1;
}
else {
res[id] = 2;
cyc = true;
}
}
col[v] = 2;
}
g[0].push([1, 0]);
g[0].push([2, 1]);
g[1].push([2, 2]);
g[1].push([3, 3]);
g[2].push([3, 4]);
g[3].push([4, 5]);
g[4].push([2, 6]);
for (let i = 0; i < n; ++i) {
if (col[i] == 0)
{
dfs(i);
}
}
document.write((cyc ? 2 : 1) + "<br>");
for (let i = 0; i < m; ++i) {
document.write(res[i] + ' ');
}
</script>
|
Performance Analysis:
- Time Complexity: As in the above approach, there is DFS Traversal of the graph which takes O(V + E) time, where V denotes the number of vertices and E denotes the number of edges. Hence the Time Complexity will be O(V + E).
- Auxiliary Space: O(1).
Share your thoughts in the comments
Please Login to comment...