Minimum cells required to reach destination with jumps equal to cell values

Difficulty Level : Medium
Last Updated : 29 Apr, 2021

Given a m x n matrix mat[][] containing positive integers. The problem is to reach to the cell (m-1, n-1) from the cell (0, 0) by following the given constraints. From a cell (i, j) one can move ‘exactly’ a distance of ‘mat[i][j]’ to the right (in the same row) or to below (in the same column) only if the movement takes to a cell within matrix boundaries.
For example: Given mat[1][1] = 4, then one can move to cells mat[1][5] and mat[5][1] only if these cells exists in the matrix. Following the constraints check whether one can reach cell (m-1, n-1) from (0, 0). 1If one can reach then print the minimum number of cells required to be covered during the movement else print “-1”.
Examples:

Input : mat[][] = { {2, 3, 2, 1, 4},
                    {3, 2, 5, 8, 2},
                    {1, 1, 2, 2, 1}  }
Output : 4
The movement and cells covered are as follows:
(0, 0)->(0, 2)
          |
        (2, 2)->(2, 4)

Input : mat[][] = { {2, 4, 2},
                {5, 3, 8},
            {1, 1, 1} }
Output : 3

Algorithm: A dynamic programming approach is given below:

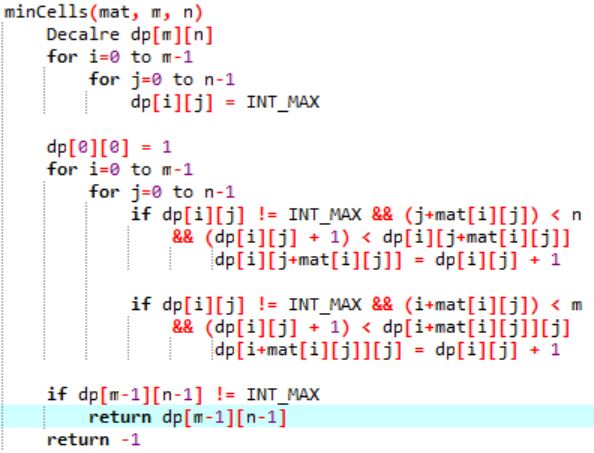
Below is the implementation of above approach:

C++

// C++ implementation to count minimum cells required
// to be covered to reach destination
#include <bits/stdc++.h>
 
using namespace std;
 
#define SIZE 100
 
// function to count minimum cells required
// to be covered to reach destination
int minCells(int mat[SIZE][SIZE], int m, int n)
{
    // to store min cells required to be
    // covered to reach a particular cell
    int dp[m][n];
 
    // initially no cells can be reached
    for (int i = 0; i < m; i++)
        for (int j = 0; j < n; j++)
            dp[i][j] = INT_MAX;
 
    // base case
    dp[0][0] = 1;
 
    // building up the dp[][] matrix
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
 
            // dp[i][j] != INT_MAX denotes that cell (i, j)
            // can be reached from cell (0, 0) and the other
            // half of the condition finds the cell on the
            // right that can be reached from (i, j)
            if (dp[i][j] != INT_MAX && (j + mat[i][j]) < n
                && (dp[i][j] + 1) < dp[i][j + mat[i][j]])
                dp[i][j + mat[i][j]] = dp[i][j] + 1;
 
            // the other half of the condition finds the cell
            // right below that can be reached from (i, j)
            if (dp[i][j] != INT_MAX && (i + mat[i][j]) < m
                && (dp[i][j] + 1) < dp[i + mat[i][j]][j])
                dp[i + mat[i][j]][j] = dp[i][j] + 1;
        }
    }
 
    // it true then cell (m-1, n-1) can be reached
    // from cell (0, 0) and returns the minimum
    // number of cells covered
    if (dp[m - 1][n - 1] != INT_MAX)
        return dp[m - 1][n - 1];
 
    // cell (m-1, n-1) cannot be reached from
    // cell (0, 0)
    return -1;
}
 
// Driver program to test above
int main()
{
    int mat[SIZE][SIZE] = { { 2, 3, 2, 1, 4 },
                            { 3, 2, 5, 8, 2 },
                            { 1, 1, 2, 2, 1 } };
 
    int m = 3, n = 5;
    cout << "Minimum number of cells = "
         << minCells(mat, m, n);
 
    return 0;
}

Java

// Java implementation to count minimum
// cells required to be covered to reach
// destination
class MinCellsDestination
{
    static final int SIZE=100;
    
    // function to count minimum cells required
    // to be covered to reach destination
    static int minCells(int mat[][], int m, int n)
    {
        // to store min cells required to be
        // covered to reach a particular cell
        int dp[][] = new int[m][n];
       
        // initially no cells can be reached
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                dp[i][j] = Integer.MAX_VALUE;
       
        // base case
        dp[0][0] = 1;
       
        // building up the dp[][] matrix
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
       
                // dp[i][j] != INT_MAX denotes that cell
                // (i, j) can be reached from cell (0, 0)
                // and the other half of the condition
                // finds the cell on the right that can
                // be reached from (i, j)
                if (dp[i][j] != Integer.MAX_VALUE &&
                   (j + mat[i][j]) < n && (dp[i][j] + 1)
                   < dp[i][j + mat[i][j]])
                    dp[i][j + mat[i][j]] = dp[i][j] + 1;
       
                // the other half of the condition finds
                // the cell right below that can be
                // reached from (i, j)
                if (dp[i][j] != Integer.MAX_VALUE &&
                   (i + mat[i][j]) < m && (dp[i][j] + 1)
                   < dp[i + mat[i][j]][j])
                    dp[i + mat[i][j]][j] = dp[i][j] + 1;
            }
        }
       
        // it true then cell (m-1, n-1) can be reached
        // from cell (0, 0) and returns the minimum
        // number of cells covered
        if (dp[m - 1][n - 1] != Integer.MAX_VALUE)
            return dp[m - 1][n - 1];
       
        // cell (m-1, n-1) cannot be reached from
        // cell (0, 0)
        return -1;
    }
     
    // Driver code
    public static void main(String args[])
    {
         int mat[][] = { { 2, 3, 2, 1, 4 },
                         { 3, 2, 5, 8, 2 },
                         { 1, 1, 2, 2, 1 }};
   
        int m = 3, n = 5;
        System.out.println("Minimum number of cells" +
                          " = " + minCells(mat, m, n));
    }
}
/* This code is contributed by Danish Kaleem */

Python3

# Python3 implementation to count minimum cells required
# to be covered to reach destination
SIZE=100
MAX=10000000
# function to count minimum cells required
# to be covered to reach destination
def minCells( mat,  m,  n):
    # to store min cells required to be
    # covered to reach a particular cell
    dp=[[MAX for i in range(n)]for i in range(m)]
   
    # initially no cells can be reached
     
    # base case
    dp[0][0] = 1
   
    # building up the dp[][] matrix
    for i in range(m):
        for j in range(n): 
            # dp[i][j] != MAX denotes that cell (i, j)
            # can be reached from cell (0, 0) and the other
            # half of the condition finds the cell on the
            # right that can be reached from (i, j)
            if (dp[i][j] != MAX and
             (j + mat[i][j]) < n and
             (dp[i][j] + 1) < dp[i][j + mat[i][j]]):
                dp[i][j + mat[i][j]] = dp[i][j] + 1
   
            # the other half of the condition finds the cell
            # right below that can be reached from (i, j)
            if (dp[i][j] != MAX and (i + mat[i][j]) < m
                and (dp[i][j] + 1) < dp[i + mat[i][j]][j]):
                dp[i + mat[i][j]][j] = dp[i][j] + 1
 
    # it true then cell (m-1, n-1) can be reached
    # from cell (0, 0) and returns the minimum
    # number of cells covered
    if (dp[m - 1][n - 1] != MAX):
        return dp[m - 1][n - 1]
   
    # cell (m-1, n-1) cannot be reached from
    # cell (0, 0)
    return -1
   
# Driver program to test above
mat= [ [ 2, 3, 2, 1, 4 ],
       [ 3, 2, 5, 8, 2 ],
       [ 1, 1, 2, 2, 1 ]]
   
m = 3
n = 5
print("Minimum number of cells = ",
     minCells(mat, m, n))
#this code is contributed by sahilshelangia

C#

// C# implementation to count minimum
// cells required to be covered to reach
// destination
using System;
 
class GFG {
     
    //static int SIZE=100;
     
    // function to count minimum cells required
    // to be covered to reach destination
    static int minCells(int [,]mat, int m, int n)
    {
         
        // to store min cells required to be
        // covered to reach a particular cell
        int [,]dp = new int[m,n];
     
        // initially no cells can be reached
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                dp[i,j] = int.MaxValue;
     
        // base case
        dp[0,0] = 1;
     
        // building up the dp[][] matrix
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
     
                // dp[i][j] != INT_MAX denotes that
                // cell (i, j) can be reached from
                // cell (0, 0) and the other half
                // of the condition finds the cell
                // on the right that can be reached
                // from (i, j)
                if (dp[i,j] != int.MaxValue &&
                (j + mat[i,j]) < n && (dp[i,j] + 1)
                < dp[i,j + mat[i,j]])
                    dp[i,j + mat[i,j]] = dp[i,j] + 1;
     
                // the other half of the condition
                // finds the cell right below that
                // can be reached from (i, j)
                if (dp[i,j] != int.MaxValue &&
                (i + mat[i,j]) < m && (dp[i,j] + 1)
                < dp[i + mat[i,j],j])
                    dp[i + mat[i,j],j] = dp[i,j] + 1;
            }
        }
     
        // it true then cell (m-1, n-1) can be
        // reached from cell (0, 0) and returns
        // the minimum number of cells covered
        if (dp[m - 1,n - 1] != int.MaxValue)
            return dp[m - 1,n - 1];
     
        // cell (m-1, n-1) cannot be reached from
        // cell (0, 0)
        return -1;
    }
     
    // Driver code
    public static void Main()
    {
        int [,]mat = { { 2, 3, 2, 1, 4 },
                       { 3, 2, 5, 8, 2 },
                       { 1, 1, 2, 2, 1 } };
 
        int m = 3, n = 5;
        Console.WriteLine("Minimum number of "
            + "cells = " + minCells(mat, m, n));
    }
}
 
// This code is contributed by anuj_67.

PHP

<?php
// PHP implementation to count
// minimum cells required to be
// covered to reach destination
 
// function to count minimum
// cells required to be
// covered to reach destination
function minCells( $mat, $m, $n)
{
     
    // to store min cells
    // required to be
    // covered to reach
    // a particular cell
    $dp =array(array());
 
    // initially no cells
    // can be reached
    for($i = 0; $i < $m; $i++)
        for($j = 0; $j < $n; $j++)
            $dp[$i][$j] = PHP_INT_MAX;
 
    // base case
    $dp[0][0] = 1;
 
    // building up the dp[][] matrix
    for($i = 0; $i < $m; $i++)
    {
        for($j = 0; $j < $n; $j++)
        {
 
            // dp[i][j] != INT_MAX
            // denotes that cell (i, j)
            // can be reached from cell
            // (0, 0) and the other half
            // of the condition finds the
            // cell on the right that can
            // be reached from (i, j)
            if ($dp[$i][$j] != PHP_INT_MAX and
                        ($j + $mat[$i][$j]) <$n
                         and ($dp[$i][$j] + 1) <
                     $dp[$i][$j + $mat[$i][$j]])
                      
                $dp[$i][$j + $mat[$i][$j]] =
                           $dp[$i][$j] + 1;
 
            // the other half of the
            // condition finds the cell
            // right below that can be
            // reached from (i, j)
            if ($dp[$i][$j] != PHP_INT_MAX and
                      ($i + $mat[$i][$j]) < $m
                      and ($dp[$i][$j] + 1) <
                      $dp[$i +$mat[$i][$j]][$j])
                       
                $dp[$i + $mat[$i][$j]][$j] = $dp[$i][$j] + 1;
        }
    }
 
    // it true then cell
    // (m-1, n-1) can be reached
    // from cell (0, 0) and
    // returns the minimum
    // number of cells covered
    if ($dp[$m - 1][$n - 1] != PHP_INT_MAX)
        return $dp[$m - 1][$n - 1];
 
    // cell (m-1, n-1) cannot
    // be reached from
    // cell (0, 0)
    return -1;
}
 
    // Driver Code
    $mat = array(array(2, 3, 2, 1, 4),
                 array(3, 2, 5, 8, 2),
                 array(1, 1, 2, 2, 1));
 
    $m = 3; $n = 5;
    echo "Minimum number of cells = "
        , minCells($mat, $m, $n);
 
// This code is contributed by anuj_67.
?>

Javascript

<script>
// Javascript implementation to count minimum
// cells required to be covered to reach
// destination
 
let SIZE=100;
      
    // function to count minimum cells required
    // to be covered to reach destination
    function minCells(mat, m, n)
    {
        // to store min cells required to be
        // covered to reach a particular cell
        let dp = new Array(m);
         
        // Loop to create 2D array using 1D array
        for (var i = 0; i < dp.length; i++) {
            dp[i] = new Array(2);
        }
         
        // initially no cells can be reached
        for (let i = 0; i < m; i++)
            for (let j = 0; j < n; j++)
                dp[i][j] = Number.MAX_VALUE;
         
        // base case
        dp[0][0] = 1;
         
        // building up the dp[][] matrix
        for (let i = 0; i < m; i++) {
            for (let j = 0; j < n; j++) {
         
                // dp[i][j] != LET_MAX denotes that cell
                // (i, j) can be reached from cell (0, 0)
                // and the other half of the condition
                // finds the cell on the right that can
                // be reached from (i, j)
                if (dp[i][j] != Number.MAX_VALUE &&
                   (j + mat[i][j]) < n && (dp[i][j] + 1)
                   < dp[i][j + mat[i][j]])
                    dp[i][j + mat[i][j]] = dp[i][j] + 1;
         
                // the other half of the condition finds
                // the cell right below that can be
                // reached from (i, j)
                if (dp[i][j] != Number.MAX_VALUE &&
                   (i + mat[i][j]) < m && (dp[i][j] + 1)
                   < dp[i + mat[i][j]][j])
                    dp[i + mat[i][j]][j] = dp[i][j] + 1;
            }
        }
         
        // it true then cell (m-1, n-1) can be reached
        // from cell (0, 0) and returns the minimum
        // number of cells covered
        if (dp[m - 1][n - 1] != Number.MAX_VALUE)
            return dp[m - 1][n - 1];
         
        // cell (m-1, n-1) cannot be reached from
        // cell (0, 0)
        return -1;
    }
   
// driver function
 
        let mat = [[ 2, 3, 2, 1, 4 ],
                         [ 3, 2, 5, 8, 2 ],
                         [ 1, 1, 2, 2, 1 ]];
     
        let m = 3, n = 5;
        document.write("Minimum number of cells" +
                          " = " + minCells(mat, m, n));
   
</script>   

Output:

Minimum number of cells = 4

Time Complexity: O(m*n)
Auxiliary Space: O(m*n)
This article is contributed by Ayush Jauhari. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.

My Personal Notes