Minimum and Maximum number of pairs in m teams of n people

There are 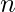people which are to be grouped into exactly 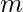teams such that there is at least one person in each team. All members of a team are friends with each other. Find the minimum and maximum no. of pairs of friends that can be formed by grouping these 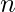people into exactly 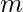teams.
Examples:

Input : 5 2 
Output : 4 6 
For maximum no. of pairs, 1st team contains only 1 member and 2nd team contains 4 people which are friends which each other, so no. of pairs in 1st team + no. of pairs in 2nd team = 0 + 6 = total pairs = 6 
For minimum no. of pairs, 1st team contains 2 members and 2nd team contains 3 people which are friends which each other, so no. of pairs in 1st team + no. of pairs in 2nd team = 1 + 3 = total pairs = 4
Input : 2 1 
Output : 1 1

Explanation:
First of all, we have to put 1 member in each team to satisfy the constraint. So we are left with people. 
1. For maximum no. of pairs
It can be seen that maximum no. pairs can result only by putting all of the remaining members of the same team. It can be explained as follows: 
Consider 2 teams one containing x people and other containing 1 person, now we have to add 1 more person to both the teams, adding him/her to the team of x people increases the no. of pairs by x while adding him to the other team only increases the no. of pairs by 1. Hence, for maximum no. of pairs, we have to put all the remaining people in the same team. 
Now the teams distribution for maximum no. of pairs would be something like this: 

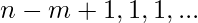
Hence, 

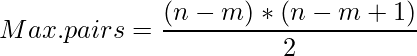
Ex: If a team consists of 3 persons, the 3rd person has 1 and 2 as friends, the 2nd person has 1 as a friend. Therefore, 2+1 = ((3-1)*(3))/2 friends
2. For minimum no. of pairs
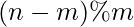
Now from the same explanation, it can be seen that minimum no. of pairs are obtained when all the persons are distributed equally in the teams. Hence remaining n-m people should be distributed in m teams so that each team contains (n-m)/m more people. Now there are people still remaining which are to be filled 1 in each team (can be seen contrary to the above condition of maximum). 
Now the team distribution for minimum no. of pairs would be something like this: 
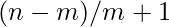
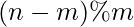
Each team has members and teams have one member extra. 
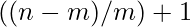
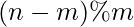
So total no. of pairs = Total no.s of pairs in m teams each of size + No. of pairs formed by adding 1 person in teams which have size 

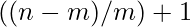
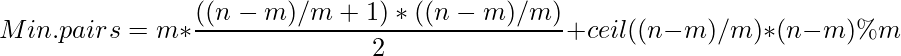
C++

// CPP program to find minimum and maximum no. of pairs
#include <bits/stdc++.h>
using namespace std;

void MinimumMaximumPairs(int n, int m)
{
    int max_pairs = ((n - m + 1) * (n - m)) / 2;

    int min_pairs = m * (((n - m) / m + 1) * ((n - m) / m)) / 2 +
                    ceil((n - m) / double(m)) * ((n - m) % m);

    cout << "Minimum no. of pairs = " << min_pairs << "\n";
    cout << "Maximum no. of pairs = " << max_pairs << "\n";
}

// Driver code
int main()
{
    int n = 5, m = 2;
    MinimumMaximumPairs(n, m);
    return 0;
}

Java

//Java  program to find minimum
// and maximum no. of pairs

import java.io.*;

class GFG {
    static void MinimumMaximumPairs(int n, int m)
{
    int max_pairs = ((n - m + 1) * (n - m)) / 2;

    int min_pairs = m * (((n - m) / m + 1) * ((n - m) / m)) / 2 +
                        (int)Math.ceil((double)((n - m) /
                                        (double)(m))) * ((n - m) % m);

        System.out.println("Minimum no. of pairs = " + min_pairs);
        System.out.println("Maximum no. of pairs = " + max_pairs);
}

// Driver code
    public static void main (String[] args) {

    int n = 5, m = 2;
    MinimumMaximumPairs(n, m);
}
}
// This code is contributed by Sachin.

Python3

# Python3 program to find minimum
# and maximum no. of pairs

from math import ceil

def MinimumMaximumPairs(n, m) :

    max_pairs = ((n - m + 1) * (n - m)) // 2;

    min_pairs = (m * (((n - m) // m + 1) *
                      ((n - m) // m)) // 2 +
                  ceil((n - m) / (m)) *
                      ((n - m) % m))

    print("Minimum no. of pairs = ", min_pairs)
    print("Maximum no. of pairs = " , max_pairs)

# Driver code
if __name__ == "__main__" :

    n ,m= 5, 2
    MinimumMaximumPairs(n, m)

# This code is contributed by Ryuga

C#

// C# program to find minimum
// and maximum no. of pairs
using System;
class GFG
{
static void MinimumMaximumPairs(int n, int m)
{
    int max_pairs = ((n - m + 1) * (n - m)) / 2;

    int min_pairs = m * (((n - m) / m + 1) * ((n - m) / m)) / 2 +
                         (int)Math.Ceiling((double)((n - m) /
                                           (double)(m))) * ((n - m) % m);

    Console.WriteLine("Minimum no. of pairs = " + min_pairs);
    Console.WriteLine("Maximum no. of pairs = " + max_pairs);
}

// Driver code
public static void Main()
{
    int n = 5, m = 2;
    MinimumMaximumPairs(n, m);
}
}

// This code is contributed by Akanksha Rai

PHP

<?php
// PHP program to find minimum
// and maximum no. of pairs
function MinimumMaximumPairs($n, $m)
{
    $max_pairs = (($n - $m + 1) * ($n - $m)) / 2;

    $min_pairs = $m * (int)((((int)($n - $m) / $m + 1) *
                             ((int)($n - $m) / $m)) / 2) +
                      (int)ceil(($n - $m) / $m) *
                               (($n - $m) % $m);

    echo("Minimum no. of pairs = " .
               "$min_pairs" . "\n");
    echo("Maximum no. of pairs = " .
                      "$max_pairs");
}

// Driver code
$n = 5; $m = 2;
MinimumMaximumPairs($n, $m);

// This code is contributed
// by Mukul Singh
?>

Javascript

<script>
// javascript  program to find minimum
// and maximum no. of pairs

    function MinimumMaximumPairs(n, m)
    {
        var max_pairs = parseInt(((n - m + 1) * (n - m)) / 2);

        var min_pairs = m * parseInt((((n - m) / m + 1) * ((n - m) / m)) / 2)
                + parseInt( Math.ceil(((n - m) /  (m)))) * ((n - m) % m);

        document.write("Minimum no. of pairs = " + min_pairs+"<br/>");
        document.write("Maximum no. of pairs = " + max_pairs);
    }

    // Driver code
    var n = 5, m = 2;
    MinimumMaximumPairs(n, m);

// This code is contributed by gauravrajput1
</script>

Output

Minimum no. of pairs =  4
Maximum no. of pairs =  6

Time Complexity: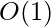

Auxiliary Space: O(1)