Minimize swaps of adjacent characters to sort every possible rearrangement of given Binary String
Last Updated :
22 Apr, 2021
Given a binary string S of length N consisting of 0s, 1s, and “?”, where “?” can be replaced by either 0 or 1, the task is to count the sum of minimum swaps of adjacent characters required to sort every possible arrangement of the string in non-decreasing order Since the answer can be very large, print it modulo 109 + 7.
Examples:
Input: S = “?0?”
Output: 3
Explanation:
Possible rearrangements of the given strings are {“101”, “100”, “000”, “001”}.
Minimum swaps to make “101” non-decreasing, i.e. “011” = 1.
Minimum swaps to make “100” non-decreasing, i.e. “001” = 2.
Minimum swaps to make “000” non-decreasing, i.e. “000” = 0.
Minimum swaps to make “001” non-decreasing, i.e. “001” = 0.
Therefore, total swaps required is 3.
Input: S = “1?00?”
Output: 17
Approach: Consider the following string representation: < Some binary string > 1 <Some string having a number of 0s and b number of ?>
- For each ‘0’ to its right, there is an inversion for every binary string generated for every question mark. So, the inversions here are a*2b.
- For the question mark, there are
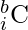 ways of choosing, such that there are i number of 0s and for each of them there are i inversions.
ways of choosing, such that there are i number of 0s and for each of them there are i inversions. - There is total of
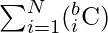
- The above expression can be transformed to b*2(b – 1). If there are no “?” in the string, the value is 0.
- There the “1” has been counted for a total of a * 2b + b*2(b – 1) inversion.
- For all “?” to the left of “1”, multiply the above value with 2, since a “?” would generate two new strings for every existing string counted.
- After traversing the whole string, return the count.
Follow the steps below to solve the problem:
- Initialize a variable count as 0 to store the sum of the total minimum swaps required for all possible strings.
- Traverse the binary string in a reverse manner.
- For every “1” in the string, calculate the product of the count of 0s and 2(count of ?), i.e. calculate the value of count as a * 2b + b * 2(b – 1).
- If the current character is “0”, then increment the count of 0s.
- Otherwise, multiply the value of count by 2 and repeat the above process.
- After completing the above steps, print the value of count as the result.
Below is the implementation of the above approach:
C++14
#include<bits/stdc++.h>
#define MOD 1000000007
using namespace std;
vector<int> MEM = { 1, 2, 4, 8, 16, 32, 64,
128, 256, 512, 1024,
2048, 4096 };
int mod_pow2(int n)
{
while (n >= MEM.size())
MEM.push_back((MEM[-1] * 2) % MOD);
return MEM[n];
}
int inversions(string bstr)
{
int total = 0, zeros = 0, questions = 0;
reverse(bstr.begin(),bstr.end());
for(char x: bstr)
{
int q;
if (x == '1')
{
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
}
else if (x == '0')
{
zeros += 1;
}
else
{
total *= 2;
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
questions += 1;
}
}
return total;
}
int main()
{
string S = "?0?";
cout << inversions(S);
}
|
Java
import java.io.*;
import java.util.*;
class GFG{
static int MOD = 1000000007;
static Integer array[] = { 1, 2, 4, 8, 16, 32, 64,
128, 256, 512, 1024,
2048, 4096 };
static Vector<Integer> MEM = new Vector<Integer>(
Arrays.asList(array));
static int mod_pow2(int n)
{
while (n >= MEM.size())
MEM.add((MEM.get(
MEM.size() - 1) * 2) % MOD);
return MEM.get(n);
}
static int inversions(char[] bstr)
{
int total = 0, zeros = 0, questions = 0;
int j = bstr.length - 1;
for(int i = 0; i < bstr.length / 2; i++)
{
char temp = bstr[i];
bstr[i] = bstr[j];
bstr[j] = temp;
j--;
}
for(char x : bstr)
{
int q;
if (x == '1')
{
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
}
else if (x == '0')
{
zeros += 1;
}
else
{
total *= 2;
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
questions += 1;
}
}
return total;
}
public static void main(String[] args)
{
char S[] = "?0?".toCharArray();
System.out.println(inversions(S));
}
}
|
Python3
MOD = 10**9 + 7
MEM = [1, 2, 4, 8, 16, 32, 64, 128,
256, 512, 1024, 2048, 4096]
def mod_pow2(n):
while n >= len(MEM):
MEM.append((MEM[-1] * 2) % MOD)
return MEM[n]
def inversions(bstr):
total, zeros, questions = (0, )*3
for x in reversed(bstr):
if x == '1':
z = zeros * mod_pow2(questions)
if questions == 0:
q = 0
else:
q = questions * mod_pow2(questions - 1)
total = (total + z + q) % MOD
elif x == '0':
zeros += 1
else:
total *= 2
z = zeros * mod_pow2(questions)
if questions == 0:
q = 0
else:
q = questions * mod_pow2(questions - 1)
total = (total + z + q) % MOD
questions += 1
return total
def main():
S = "?0?"
print(inversions(S))
if __name__ == "__main__":
main()
|
C#
using System;
using System.Collections.Generic;
class GFG {
static int MOD = 1000000007;
static List<int> MEM = new List<int>(new int[] { 1, 2, 4, 8, 16, 32, 64,
128, 256, 512, 1024,
2048, 4096 });
static int mod_pow2(int n)
{
while (n >= MEM.Count)
MEM.Add((MEM[MEM.Count - 1] * 2) % MOD);
return MEM[n];
}
static int inversions(char[] bstr)
{
int total = 0, zeros = 0, questions = 0;
Array.Reverse(bstr);
foreach(char x in bstr)
{
int q;
if (x == '1')
{
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
}
else if (x == '0')
{
zeros += 1;
}
else
{
total *= 2;
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
questions += 1;
}
}
return total;
}
static void Main()
{
char[] S = "?0?".ToCharArray();
Console.WriteLine(inversions(S));
}
}
|
Javascript
<script>
let MOD = 1000000007;
let MEM = [ 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096 ];
function mod_pow2(n)
{
while (n >= MEM.length)
MEM.push((MEM[MEM.length - 1] * 2) % MOD);
return MEM[n];
}
function inversions(bstr)
{
let total = 0, zeros = 0, questions = 0;
bstr.reverse();
for(let i = 0; i < bstr.length; i++)
{
let q;
if (bstr[i] == '1')
{
let z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(questions - 1);
total = (total + z + q) % MOD;
}
else if (bstr[i] == '0')
{
zeros += 1;
}
else
{
total *= 2;
let z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(questions - 1);
total = (total + z + q) % MOD;
questions += 1;
}
}
return total;
}
let S = "?0?".split('');
document.write(inversions(S));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...