Mensuration 3D Formulas and Aptitude Questions
Last Updated :
10 Mar, 2023
Mensuration 3D is all about measuring and calculating the size and volume of objects in three dimensions. This branch of mathematics involves using the Mensuration 3D Formula and Quantitative Aptitude skills to determine the size, volume, and surface area of shapes such as cubes, spheres, cones, frustum, prism, pyramids, and cylinders. In this article, learn the concepts and formulas of 3D mensuration, where you can solve a wide range of questions, and tips and tricks.
Practice Quiz:
Practice Mensuration 3D Aptitude Quiz Question
Cuboid
Let the length, breadth, and height of the cuboid be ‘L’, ‘B’, and ‘H’ respectively.

- Volume = L x B x H
- Curved Surface area = 2 H (L + B)
- Total surface area = 2 (L B + B H + H L)
- Length of diagonal = (L2 + B2 + H2)1/2
Cube
Let the side of the cube be ‘a’

- Volume = a3
- Curved Surface area = 4 a2
- Total surface area = 6 a2
- Length of diagonal =
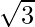 a
a
Cylinder (Right Circular Cylinder)
Let the radius of the base and height of the right circular cylinder be ‘R’ and ‘H’ respectively.

- Volume = π R2 H
- Curved Surface area = 2 π R H
- Total surface area = 2 π R H + 2 π R2
Hollow Cylinder (Hollow Right Circular Cylinder)
Let the inner radius of the base, outer radius of the base and height of the hollow right circular cylinder be ‘r’, ‘R’ and ‘H’ respectively.

- Volume = π H (R2 – r2)
- Curved Surface area = 2 π R H + 2 π r H = 2 π H (R + r)
- Total surface area = 2 π H (R + r) + 2 π (R2 – r2)
Cone
Let the radius of the base, slant height and height of the cone be ‘R’, ‘L’ and ‘H’ respectively.

- L2 = R2 + H2
- Volume = π R2 H / 3
- Curved Surface area = π R L
- Total surface area = π R L + π R2
Sphere
Let the radius of the sphere be ‘R’

- Volume = (4 / 3) π R3
- Surface area = 4 π R2
Hemisphere
Let the radius of the hemisphere be ‘R’

- Volume = (2 / 3) π R3
- Curved Surface area = 2 π R2
- Total Surface area = 3 π R2
Note: Please note that whenever it is mentioned to find “Surface Area”, we calculate the total surface area.
Mensuration 3D Formulas
Here are some important formulas, we must consider while solving mensuration 3D questions.
Shape | Volume Formula | Curved Surface Area Formula | Total Surface Area Formula |
Cube
| V = s³ (where s is the length of one side)
| CSA = 4s² (where s is the length of one side)
| TSA = 6s² (where s is the length of one side)
|
Cuboid
| V = lwh (where l is the length, w is the width, h is the height)
| CSA = 2lh + 2wh (where l is the length, w is the width, h is the height)
| TSA = 2lw + 2lh + 2wh (where l is the length, w is the width, h is the height)
|
Cylinder
| V = πr²h (where r is the radius, h is the height)
| CSA = 2πrh (where r is the radius, h is the height)
| TSA = 2πr(h + r) (where r is the radius, h is the height)
|
Cone
| V = (1/3)πr²h (where r is the radius, h is the height)
| CSA = πrl (where r is the radius, l is the slant height)
| TSA = πr(r + l) (where r is the radius, l is the slant height)
|
Sphere
| V = (4/3)πr³ (where r is the radius)
| CSA = 4πr² (where r is the radius)
| TSA = 4πr² (where r is the radius)
|
Hemisphere
| V = (2/3)πr³ (where r is the radius)
| CSA = 2πr² (where r is the radius)
| TSA = 3πr² (where r is the radius)
|
Sample Questions on Mensuration 3D
Q1: Find the length of the largest rod that can be kept in a cuboidal room of dimensions 10 x 15 x 6 m.
Solution :
Largest rod would lie along the diagonal.
=> Length of largest rod = Length of diagonal of the room = (L2 + B2 + H2)1/2
=> Length of the largest rod = (102 + 152 + 62)1/2 = (100 + 225 + 36)1/2 = (361)1/2
=> Length of the largest rod = 19 m
Q2: Find the number of bricks of dimension 24 x 12 x 8 cm each that would be required to make a wall 24 m long, 8 m high and 60 cm thick.
Solution :
Volume of 1 brick = 24 x 12 x 8 = 2304 cm 3
Volume of wall = 2400 x 800 x 60 = 115200000 cm 3
Therefore, number of bricks required = 115200000 / 2304 = 50000
Q3: A rectangular sheet of paper measuring 22 cm x 7 cm is rolled along the longer side to make a cylinder. Find the volume of the cylinder formed.
Solution:
Let the radius of the cylinder be ‘R’.
The sheet is rolled along the longer side.
=> 2 π R = 22
=> R = 3.5 cm
Also, height = 7 cm
Therefore, volume of the cylinder = π R2 H = π (3.5)2 7 = 269.5 cm3
Q4: If each edge of a cube is increased by 10 %, what would be the percentage increase in volume?
Solution:
Let the original edge length be ‘a’
=> Original volume = a3
Now, new edge length = 1.1 a
=> New volume = (1.1 a)3 = 1.331 a3
=> Increase in volume = 1.331 a3 – 1 a3 = 0.331 a3
Therefore, percentage increase int eh volume = (0.331 a3 / a3) x 100 = 33.1 %
Q5: Three metal cubes of edge lengths 3 cm, 4 cm, and 5 cm are melted to form a single cube. Find the edge length of such a cube.
Solution:
Volume of new cube = Volume of metal generated on melting the cubes = Sum of volumes of the three cubes
=> Volume of new cube = 3 3 + 4 3 + 5 3 = 216
=> Edge length of new cube = (216)1/3 = 6 cm
Q6: Find the length of a 1.25 m wide metal sheet required to make a conical machine of radius 7 m and height 24 m.
Solution:
The sheet would be shaped into a cone.
=> Area of sheet = Area of conical machine
=> 1.25 x Length = π x R x L
=> 1.25 x Length = π x R x (72 + 242)1/2
=> 1.25 x Length = π x 7 x 25
=> Length = 440 m
Thus, 440 m long metal sheet is required to make the conical machine.
Q7: From a cylindrical vessel having a radius of the base of 7 cm and a height 6cm, water is poured into small hemispherical bowls each of radius 3.5 cm. Find the minimum number of bowls that would be required to empty the cylindrical vessel.
Solution :
Volume of cylindrical vessel = π R2 H = π (72) 6 = 924 cm3
Volume of each bowl = (2 / 3) π R3 = (2 / 3) π 3.53 = 269.5 / 3
=> Number of bowls required = (924) / (269.5 / 3) = 10.28
But since a number of bowls cannot be in fractions, we need at least 11 such bowls to empty the cylindrical vessel.
Related Resources:
Problems on Mensuration 3D | Set-2
Test your knowledge of Mensuration 3D in Quantitative Aptitude with the quiz linked below, containing numerous practice questions to help you master the topic:-
<<Practice Mensuration 3D Aptitude Questions>>
Also Practice
Share your thoughts in the comments
Please Login to comment...