Vieta’s Formulas
Last Updated :
13 Mar, 2023
Vieta’s formula relates the coefficients of polynomial to the sum and product of their roots, as well as the products of the roots taken in groups. Vieta’s formula describes the relationship of the roots of a polynomial with its coefficients. Consider the following example to find a polynomial with given roots. (Only discuss real-valued polynomials, i.e. the coefficients of polynomials are real numbers). Let’s take a quadratic polynomial. Given two real roots 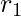 and
and 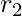 , then find a polynomial.
, then find a polynomial.
Consider the polynomial 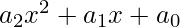 . Given the roots, we can also write it as
. Given the roots, we can also write it as
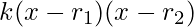 .
.
Since both equation represents the same polynomial, so equate both polynomial
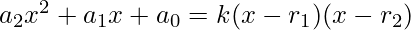
Simplifying the above equation, we get
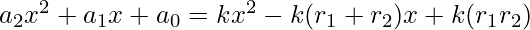
Comparing the coefficients of both sides, we get
For 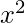 ,
, 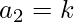 ,
,
For 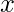 ,
, 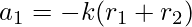 ,
,
For constant term, 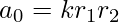 ,
,
Which gives,
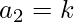 ,
,
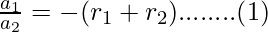

Equation (1) and (2) are known as Vieta’s Formulas for a second degree polynomial.
In general, for an 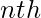 degree polynomial, there are n different Vieta’s Formulas. They can be written in a condensed form as
degree polynomial, there are n different Vieta’s Formulas. They can be written in a condensed form as
For 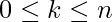
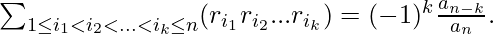
The following examples illustrate the use of Vieta’s formula to solve a problem.
Examples:
Input : n = 2
roots = {-3, 2}
Output : Polynomial coefficients: -6, -1, 1
Input : n = 4
roots = {-1, 2, -3, 7}
Output : Polynomial coefficients: 42 -29 -19 5 1
C++
#include <bits/stdc++.h>
using namespace std;
void vietaFormula(int roots[], int n)
{
int coeff[n + 1];
memset(coeff, 0, sizeof(coeff));
coeff[0] = 1;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j > 0; j--) {
coeff[j] += roots[i] * coeff[j - 1];
}
}
cout << "Polynomial Coefficients: ";
for (int i = n; i >= 0; i--) {
cout << coeff[i] << " ";
}
}
int main()
{
int n = 4;
int roots[] = { -1, 2, -3, 7 };
vietaFormula(roots, n);
return 0;
}
|
Java
import java.util.*;
public class Main {
public static void vietaFormula(int[] roots, int n)
{
int[] coeff = new int[n + 1];
Arrays.fill(coeff, 0);
coeff[0] = 1;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j > 0; j--) {
coeff[j] += roots[i] * coeff[j - 1];
}
}
System.out.print("Polynomial Coefficients: ");
for (int i = n; i >= 0; i--) {
System.out.print(coeff[i] + " ");
}
}
public static void main(String[] args)
{
int n = 4;
int[] roots = { -1, 2, -3, 7 };
vietaFormula(roots, n);
}
}
|
Python3
def vieta_formula(roots, n):
coeff = [0] * (n + 1)
coeff[0] = 1
for i in range(n):
for j in range(i + 1, 0, -1):
coeff[j] += roots[i] * coeff[j - 1]
return coeff[::-1]
def main():
n = 4
roots = [-1, 2, -3, 7]
coefficients = vieta_formula(roots, n)
print("Polynomial Coefficients: ", coefficients)
if __name__ == "__main__":
main()
|
C#
using System;
public class Program
{
public static void vietaFormula(int[] roots, int n)
{
int[] coeff = new int[n + 1];
Array.Fill(coeff, 0);
coeff[0] = 1;
for (int i = 0; i < n; i++)
{
for (int j = i + 1; j > 0; j--)
{
coeff[j] += roots[i] * coeff[j - 1];
}
}
Console.Write("Polynomial Coefficients: ");
for (int i = n; i >= 0; i--)
{
Console.Write(coeff[i] + " ");
}
}
public static void Main(string[] args)
{
int n = 4;
int[] roots = { -1, 2, -3, 7 };
vietaFormula(roots, n);
}
}
|
Javascript
function vietaFormula(roots, n)
{
let coeff = new Array(n + 1).fill(0);
coeff[0] = 1;
for (let i = 0; i < n; i++) {
for (let j = i + 1; j > 0; j--) {
coeff[j] += roots[i] * coeff[j - 1];
}
}
console.log("Polynomial Coefficients: ");
for (let i = n; i >= 0; i--) {
console.log(coeff[i] + " ");
}
}
function main()
{
let n = 4;
let roots = [ -1, 2, -3, 7 ];
vietaFormula(roots, n);
return 0;
}
main();
|
OutputPolynomial Coefficients: 42 -29 -19 5 1
Time Complexity : 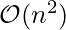 .
.
Auxiliary Space: O(n) because it is using extra space for array coeff
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...