Measuring Internal Resistance of a Cell
Last Updated :
10 Dec, 2021
Usually while studying the theory behind the electrical circuits it is assumed that all the components of the circuits are ideal. In an ideal state, the battery of the system is assumed to have zero resistance. But in reality, it is not the case. While working with batteries in real life, it s noticed that they have some internal resistance which affects the current in the circuit. Sometimes it is not specified on the battery and it changes as the battery discharges. In that case, it becomes essential to calculate the internal resistance of the battery being used. Let’s look at how it’s done in detail.
Internal Resistance of a Battery
It is known that a large emf-based battery has more size than the batteries with less emf. These batteries contain more energy and thus can deliver larger currents. Notice that a 12V battery of a truck can deliver more current than a 12V battery present in a motorcycle. The reason behind this can be attributed to the fact that the battery of the truck has less internal resistance than the battery of a motorcycle.
Internal resistance is the inherent resistance that is present inside a voltage source.

The figure above shows two fundamental parts of a voltage source. The emf present inside the battery and the resistance. This emf is denoted by E while the internal resistance is denoted by r, both of them are series. The smaller the internal resistance for the battery, the more current it is able to supply to the circuit. The internal resistance of a battery can behave in complex ways, as the battery depletes the internal resistance of the battery increases. But it may also depend on the magnitude and the direction of the electric current through a voltage source, its temperature, and even the material the battery is made up of.
Potentiometer
Potential is used to measure the potential difference between two points. It is sometimes also used to compare the e.m.f of two cells or measure the internal resistance of a battery. At a structural level, it is a device that consists of a long wire of uniform cross-sectional area and of 10m in length. While using a potentiometer, one should make sure that the wire that is begin used in the device should have a uniform cross-sectional area and low resistivity, and high-temperature coefficient. The wires are stretched parallel to each other and are joined in series through the copper strips. A meter scale is also attached to the wooden board.
Relation between E.M.F and Potential Difference Across a Cell
Let’s consider a cell with e.m.f “E” and internal resistance “r”. The cell is connected to an external resistance of “R”. In that case, the total resistance of the circuit becomes R + r. The current I in the circuit now will be given by,
I = E/(R+ r)
⇒ E = I (R + r)
Thus, the potential across the external resistance,
V = IR = E – Ir
This equation shows that V is less than the e.m.f of the cell. This fall in the potential is due to the potential drop in the internal resistance of the battery. The equation given above can be rearranged as,
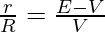
The internal resistance will be given by,
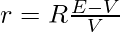
Rheostat can be adjusted on the potentiometer to obtain the balancing lengths l1 and l2 for open and closed circuits respectively. The figure shows this setting,

Let “k” be the potential gradient on the wire on the potentiometer.
E = kl1 and V = kl2
The above equation for the internal resistance can be modified by,
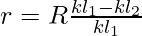
⇒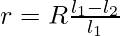
Sample Problems
Question 1: Find the current that will flow inside the battery of 10 Volts and 0.04 ohms internal resistances in case its terminals are connected with each other.
Answer:
The current in that case will be given by simple application of ohm’s law.
V = 10V
r = 0.04 ohms.
V = IR
Plugging the values in the equation,
I = V/R
⇒ I = 10/0.04
⇒ I = 250 A
Question 2: Find the current that will flow inside the battery of 40 Volts and 10 ohms internal resistances in case its terminals are connected with each other. Find the terminal voltage of the battery.
Answer:
The current in that case will be given by simple application of ohm’s law.
V = 40 V
R= 10 ohms.
V = IR
Plugging the values in the equation,
I = V/R
⇒ I = 40/10
⇒ I = 4 A
The terminal voltage of the battery is given by,
V = emf – Ir
Given , emf = 40 V, I = 4A and r = 10
V = emf – Ir
⇒ V = 40 – (4)(10)
⇒ V = 0 V
Question 3: Find the current that will flow inside the battery of 20 Volts and 4 ohms internal resistances and 6 ohms load resistance in series. Find the terminal voltage of the battery.
Answer:
The current in that case will be given by simple application of ohm’s law.
I = 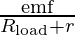
emf = 20 V
Rload= 6 ohms.
r = 4
plugging the values in the equation,
I = 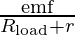
⇒ I = 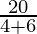
⇒ I = 2 A
The terminal voltage of the battery is given by,
V = emf – Ir
Given, emf = 20V, I = 2A and r = 4
V = emf – Ir
⇒ V = 20 – (2)(4)
⇒ V = 20 – 8
⇒ V = 12V
Question 4: Find the internal resistance of the battery if the potentiometer is balanced at lengths l2 = 120cm and l1 = 300 cm from one end. Assume the external resistance is 10 Ohms.
Answer:
The internal resistance when measured through potentiometer is given by,
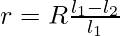
Given:
l1 = 300 cm
l2 = 120 cm
R = 10
Plugging the values in the equation,
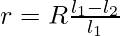
⇒ 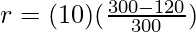
⇒ 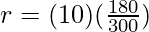
⇒ r = 6 Ohms
Question 5: Find the internal resistance of the battery if the potentiometer is balanced at lengths l2 = 60cm and l1 = 150 cm from one end. Assume the external resistance is 20 Ohms.
Answer:
The internal resistance when measured through potentiometer is given by,
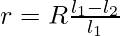
Given:
l1 = 60 cm
l2 = 150 cm
R = 20
Plugging the values in the equation,
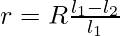
⇒ 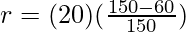
⇒ 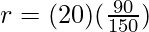
⇒ r = 6 Ohms
Share your thoughts in the comments
Please Login to comment...