We use general things around us that are moving, like if we see around us, monitor air moving around us, like we have clocks with the hands moving, we all know that day and night is caused because of motion of Earth around the Sun, yet seasons are caused because of it. So we are going to study in detail about what exactly the term motion is?
To recognize more about motion or rest we should first get known with the term reference point or stationary object. To comment on the state of any object, we have to consider a reference point or stationary object or surroundings. In this reference point, the stationary object does not change its position.
For Example: If we consider a pole and a car, then a pole will be stationary as it can’t change its location, but the car can alter. So, to say that car is at rest or motion we need to consider its motion concerning that of the pole or any other stationary object. This stationary object can also be called a reference point.
Rest and Motion
Let us consider a car standing in front of the house. Let’s say primarily it is at location A then after some time, it moves to location B. That means it has changed its position concerning the stationary object that is the house.
And if that car keeps on standing at position A that means it hasn’t changed its position concerning the house that means it is at rest so here we define the terms rest and motion.
Rest: When a body doesn’t change its position for its surroundings or reference point, then the body is said to be at rest.
Motion: When the body changes its position to its surroundings or reference point, then the body is in motion.
So, we can say that when an object is moving or in motion, it possesses the following characteristics as given below.
Characteristics of a moving object:
The moving object changes its position with time. Now we have seen that movement of the car can be easily seen that is we don’t have to concentrate much but to know the movement of an arm of clock let’s say hour hand we need to keep verify this is because some motion is that quick that we can see it happening, on the other hand, some motion is so slow that it can’t be seen undoubtedly.
We can elaborate it as: Our wristwatch has three hands: minute, seconds and hour hand .out of them second-hand moves fast that its motion can be seen but to see the motion in hour hand and minute hand we have to keep the track as the motion in them is moderately slow.
Types of Motion
We come across different types of motions like
- Linear: Motion where we move in a straight line is called linear motion. For example, driving on straight roads.
- Rotational: We all know the earth rotates on its axis which causes day and night that progress is rotational motion because it is rotating on its axis so, we can define it as the rotational motion when the body rotates about a fixed axis.
- Circular: We all encounter roundabouts on-road and when we are driving we can’t drive straight through it, we have to take the arched path that is the circular motion. So, if the body travels along a curved path, it is said to be in circular motion.
- Vibratory: Everyone must have played with the instrument guitar. So, what happens when you hit it with your finger, its string starts vibrating and thus the sound is created. That motion is vibratory as it is caused due to vibratory motion of particles, so it is when the body shows to and from movements.
Scalar and Vector Physical Quantities
We learn so many physical quantities like distance, velocity and many more. All these quantities are mostly classified under two categories that is scalar or vector depending upon whether they provide the complete information about the magnitude (value) and direction or give the unfinished information like only direction or only value.
Scalar Quantities
The quantities that depend upon the magnitude and not the direction is called scalar quantities. They are represented as their symbol.
For Example: If you voyage to Delhi to your relative’s place and if somebody asks you about the distance what do you reply. We say it was like a 250km run from Chandigarh. You don’t tell him that 25km towards the east, then west. We just say 250km that means we explain it only in magnitude, and we don’t identify directions. So, it is a scalar quantity.
Vector Quantities
The physical quantities depend upon magnitude as well as direction. They are represented by putting an arrow on their symbol.
For Example: Now if you voyage a straight short path in a specific way then we can say that I travelled 25km towards the east. So, in this case, the direction is specified, so it falls in the category of a vector quantity.
Reference point and reference frame
- To explain the position of an object we require a reference point or origin. An object may appear to be moving to one observer and stationary to another.
- Example: A traveller inside a bus sees the other passengers be at rest, whereas a spectator outside the bus sees the passengers are in motion.
- A convention or a common reference point or frame is needed, to make observations easy. All substance must be in the same reference frame.
Distance and Displacement
The magnitude of the length enclosed by a moving entity is called distance. It has no direction. Displacement is the shortest distance between two points or the distance between the starting and final positions concerning time. It has magnitude as well direction. Displacement can be zero, but distance cannot.

Magnitude
The size or extent of a physical quantity is magnitude. In physics, we have scalar and vector quantities. Scalar quantities are only expressed as magnitude. E.g: time, distance, mass, temperature, area, volume.
Vector quantities are articulated in magnitude as well as the direction of the entity. E.g: Velocity, displacement, weight, momentum, force, acceleration, etc.
Time, Average Speed and Velocity
Time and speed
Time is the period of an incident that is articulated in seconds. Most physical phenomena occur in time. It is a scalar quantity. Speed is the rate of change of distance. If a body covers a certain distance in a certain amount of time, its speed is known by
Speed 
Average speed = Total distance travelled/Total time taken
Uniform motion and non-uniform motion:
When an object covers the same distances in the same intervals of time it is in uniform motion. An entity said to be in non-uniform motion when it covers unequal distances in equal intervals of time.
Velocity
The rate of change of displacement is velocity. It is a vector quantity. Here the direction of motion is specified.
Velocity 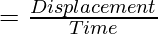
Average velocity = (Initial Velocity + Final Velocity)/2
Acceleration
Acceleration is the rate of change of velocity. It is a vector quantity. Velocity varies with time in non-uniform motion, i.e., change in velocity is not 0. It is denoted by “a”.
Acceleration = Change in Velocity/Time
or
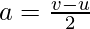
Where, v(final velocity), t(time taken), and u(initial velocity).
Graphical Representation of Motion
Graphical representation of motion is representation of motion using graphs that show the relationship between various parameters such as time, displacement, velocity, and acceleration. Here are some common types of graphs used to represent motion.
Distance-Time graph:
- Distance-Time graphs show the change in position of an object for time.
- Linear variation = non-linear variations and uniform motion imply non-uniform motion
- The slope gives us speed

- As the slope is constant OA implies uniform motion with constant speed.
- AB implies the body is at rest as the slope is zero
- B to C is non-uniform motion
Velocity-Time Graph:
- Velocity-Time graphs show the change in velocity concerning time.
- Slope gives acceleration
- The displacement is given by the area below the curve.
- Line parallel to x-axis implies constant velocity.

- OA = constant acceleration, AB = constant velocity, BC = constant retardation
Also Read,
Equations of Motion
The motion of an entity moving at uniform acceleration can be described with the assist of three equations, namely
(i) v = u + at
(ii)
(iii) 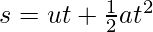
Uniform Circular Motion
- It is called uniform circular motion if an object moves in a circular path with uniform speed.
- Velocity is varying as direction keeps altering.
- Acceleration is constant.
Sample Questions
Question 1. Two cars F and M race each other. The Car F drove for 2 minutes at a speed of 7.2 km/h, rested for 56 minutes and again ran for 2 minutes at a speed of 7.2 km/h. Find the average speed of the car F in the race.
Answer:
We know that
Distance= speed×time
Distance travelled in first 2 minute 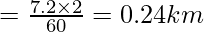
Total distance = 0.24 + 0.24 = 0.48 km
Total time = 2+2+56 = 60 minute = 1 hr
Average speed =  =0.48 km/h
=0.48 km/h
Question 2. A train 200 m long is moving with a velocity of 72 km/hr. Find the time it takes to cross the bridge which is 1 km long?
Answer:
Given Length of Train = 200m, velocity = 72 km/hr = 20 m/s, Length of the Bridge =1 Km.
Total distance covered by the train to fully pass the bridge = 1000 + 200 = 1200 m
So, time taken
Time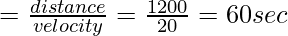
Question 3. An object travels 26 m in 4 s and then another 22m in 3s. What is the average speed of the object?
Answer:
Total distance travelled by the object =26 m + 22 m = 48 m
Total time taken = 4 s + 3 s = 7 s
Average Speed = total distance travelled/total time taken
Average Speed 6m/s
6m/s
Question 4. Stopping distance of vehicles: When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity (v_{0}) and the braking capacity, or deceleration, that is caused by the braking. A car travelling at a speed of 72km/hr suddenly applies the brake with a deceleration of 10m/s2. Find the stopping distance of the car.
Answer:
Here u=72 km/hr  m/s = 20 m/s, v=0
m/s = 20 m/s, v=0
a= -10 m/s2
Now using the relation
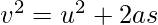
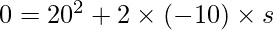
s = 20m
Question 5. A train starts from rest and accelerate uniformly at the rate of 10 m/s2 for 5 sec. Calculate the velocity of train in 5 sec.
Answer:
Here u=0, a= 10m/s2, t= 5 sec, v=?
Now v= u + at
v = 0+10×5= 50 m/s
Question 6. An electron moving with a velocity of 5 × 103 m/s enters into a consistent field and acquires a consistent acceleration of 2 ×103 m/s2 within the direction of the initial velocity.
i. Determine the time during which electron velocity is going to be doubled?
ii. How much distance electron would cover at this time?
Answer:
Given u =  m/s2
m/s2
 m/s
m/s
i. Using v = u + at
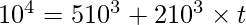
or, t = 2.5 sec
ii. Using


Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...