Maximize the sum of products of the degrees between any two vertices of the tree
Last Updated :
15 Sep, 2022
Given an integer N, the task is to construct a tree such that the sum of 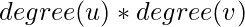 for all ordered pairs (u, v) is the maximum where u != v. Print the maximum possible sum.
for all ordered pairs (u, v) is the maximum where u != v. Print the maximum possible sum.
Examples:
Input: N = 4
Output: 26
1
/
2
/
3
/
4
For node 1, 1*2 + 1*2 + 1*1 = 5
For node 2, 2*1 + 2*2 + 2*1 = 8
For node 3, 2*1 + 2*2 + 2*1 = 8
For node 4, 1*1 + 1*2 + 1*2 = 5
Total sum = 5 + 8 + 8 + 5 = 26
Input: N = 6
Output: 82
Approach: We know that sum of the degree of all nodes in a tree is (2 * N) – 2 where N is the number of nodes in the tree. As we have to maximize the sum, we have to minimize the number of leaf nodes, as the leaf nodes have the minimum degree among all the nodes of the tree and the tree will be of the form:
1
/
2
/
...
/
N
where only the root and the only leaf node will have a degree of 1 and all the other nodes will have degree 2.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
ll maxSum(int N)
{
ll ans = 0;
for (int u = 1; u <= N; u++) {
for (int v = 1; v <= N; v++) {
if (u == v)
continue;
int degreeU = 2;
if (u == 1 || u == N)
degreeU = 1;
int degreeV = 2;
if (v == 1 || v == N)
degreeV = 1;
ans += (degreeU * degreeV);
}
}
return ans;
}
int main()
{
int N = 6;
cout << maxSum(N);
}
|
Java
class GFG
{
static int maxSum(int N)
{
int ans = 0;
for (int u = 1; u <= N; u++)
{
for (int v = 1; v <= N; v++)
{
if (u == v)
continue;
int degreeU = 2;
if (u == 1 || u == N)
degreeU = 1;
int degreeV = 2;
if (v == 1 || v == N)
degreeV = 1;
ans += (degreeU * degreeV);
}
}
return ans;
}
public static void main(String[] args)
{
int N = 6;
System.out.println(maxSum(N));
}
}
|
Python3
def maxSum(N) :
ans = 0;
for u in range(1, N + 1) :
for v in range(1, N + 1) :
if (u == v) :
continue;
degreeU = 2;
if (u == 1 or u == N) :
degreeU = 1;
degreeV = 2;
if (v == 1 or v == N) :
degreeV = 1;
ans += (degreeU * degreeV);
return ans;
if __name__ == "__main__" :
N = 6;
print(maxSum(N));
|
C#
using System;
class GFG
{
static int maxSum(int N)
{
int ans = 0;
for (int u = 1; u <= N; u++)
{
for (int v = 1; v <= N; v++)
{
if (u == v)
continue;
int degreeU = 2;
if (u == 1 || u == N)
degreeU = 1;
int degreeV = 2;
if (v == 1 || v == N)
degreeV = 1;
ans += (degreeU * degreeV);
}
}
return ans;
}
static void Main()
{
int N = 6;
Console.WriteLine(maxSum(N));
}
}
|
PHP
<?php
function maxSum($N)
{
$ans = 0;
for ($u = 1; $u <= $N; $u++)
{
for ($v = 1; $v <= $N; $v++)
{
if ($u == $v)
continue;
$degreeU = 2;
if ($u == 1 || $u == $N)
$degreeU = 1;
$degreeV = 2;
if ($v == 1 || $v == $N)
$degreeV = 1;
$ans += ($degreeU * $degreeV);
}
}
return $ans;
}
$N = 6;
echo maxSum($N);
?>
|
Javascript
<script>
function maxSum(N)
{
var ans = 0;
for (var u = 1; u <= N; u++) {
for (var v = 1; v <= N; v++) {
if (u == v)
continue;
var degreeU = 2;
if (u == 1 || u == N)
degreeU = 1;
var degreeV = 2;
if (v == 1 || v == N)
degreeV = 1;
ans += (degreeU * degreeV);
}
}
return ans;
}
var N = 6;
document.write( maxSum(N));
</script>
|
Complexity Analysis:
- Time Complexity: O(N2)
- Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...