Longest Zig-Zag Subsequence
Last Updated :
20 Dec, 2022
The longest Zig-Zag subsequence problem is to find length of the longest subsequence of given sequence such that all elements of this are alternating.
If a sequence {x1, x2, .. xn} is alternating sequence then its element satisfy one of the following relation :
x1 < x2 > x3 < x4 > x5 < …. xn or
x1 > x2 < x3 > x4 < x5 > …. xn
Examples :
Input: arr[] = {1, 5, 4}
Output: 3
The whole arrays is of the form x1 < x2 > x3
Input: arr[] = {1, 4, 5}
Output: 2
All subsequences of length 2 are either of the form
x1 < x2; or x1 > x2
Input: arr[] = {10, 22, 9, 33, 49, 50, 31, 60}
Output: 6
The subsequences {10, 22, 9, 33, 31, 60} or
{10, 22, 9, 49, 31, 60} or {10, 22, 9, 50, 31, 60}
are longest Zig-Zag of length 6.
This problem is an extension of longest increasing subsequence problem, but requires more thinking for finding optimal substructure property in this.
We will solve this problem by dynamic Programming method, Let A is given array of length n of integers. We define a 2D array Z[n][2] such that Z[i][0] contains longest Zig-Zag subsequence ending at index i and last element is greater than its previous element and Z[i][1] contains longest Zig-Zag subsequence ending at index i and last element is smaller than its previous element, then we have following recurrence relation between them,
Z[i][0] = Length of the longest Zig-Zag subsequence
ending at index i and last element is greater
than its previous element
Z[i][1] = Length of the longest Zig-Zag subsequence
ending at index i and last element is smaller
than its previous element
Recursive Formulation:
Z[i][0] = max (Z[i][0], Z[j][1] + 1);
for all j < i and A[j] < A[i]
Z[i][1] = max (Z[i][1], Z[j][0] + 1);
for all j < i and A[j] > A[i]
The first recurrence relation is based on the fact that, If we are at position i and this element has to bigger than its previous element then for this sequence (upto i) to be bigger we will try to choose an element j ( < i) such that A[j] < A[i] i.e. A[j] can become A[i]’s previous element and Z[j][1] + 1 is bigger than Z[i][0] then we will update Z[i][0].
Remember we have chosen Z[j][1] + 1 not Z[j][0] + 1 to satisfy alternate property because in Z[j][0] last element is bigger than its previous one and A[i] is greater than A[j] which will break the alternating property if we update. So above fact derives first recurrence relation, similar argument can be made for second recurrence relation also.
C++
#include <bits/stdc++.h>
using namespace std;
int max(int a, int b) { return (a > b) ? a : b; }
int zzis(int arr[], int n)
{
int Z[n][2];
for (int i = 0; i < n; i++)
Z[i][0] = Z[i][1] = 1;
int res = 1;
for (int i = 1; i < n; i++)
{
for (int j = 0; j < i; j++)
{
if (arr[j] < arr[i] && Z[i][0] < Z[j][1] + 1)
Z[i][0] = Z[j][1] + 1;
if( arr[j] > arr[i] && Z[i][1] < Z[j][0] + 1)
Z[i][1] = Z[j][0] + 1;
}
if (res < max(Z[i][0], Z[i][1]))
res = max(Z[i][0], Z[i][1]);
}
return res;
}
int main()
{
int arr[] = { 10, 22, 9, 33, 49, 50, 31, 60 };
int n = sizeof(arr)/sizeof(arr[0]);
cout<<"Length of Longest Zig-Zag subsequence is "<<zzis(arr, n)<<endl;
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
int max(int a, int b) { return (a > b) ? a : b; }
int zzis(int arr[], int n)
{
int Z[n][2];
for (int i = 0; i < n; i++)
Z[i][0] = Z[i][1] = 1;
int res = 1;
for (int i = 1; i < n; i++)
{
for (int j = 0; j < i; j++)
{
if (arr[j] < arr[i] && Z[i][0] < Z[j][1] + 1)
Z[i][0] = Z[j][1] + 1;
if( arr[j] > arr[i] && Z[i][1] < Z[j][0] + 1)
Z[i][1] = Z[j][0] + 1;
}
if (res < max(Z[i][0], Z[i][1]))
res = max(Z[i][0], Z[i][1]);
}
return res;
}
int main()
{
int arr[] = { 10, 22, 9, 33, 49, 50, 31, 60 };
int n = sizeof(arr)/sizeof(arr[0]);
printf("Length of Longest Zig-Zag subsequence is %d\n",
zzis(arr, n) );
return 0;
}
|
Java
import java.io.*;
class GFG {
static int zzis(int arr[], int n)
{
int Z[][] = new int[n][2];
for (int i = 0; i < n; i++)
Z[i][0] = Z[i][1] = 1;
int res = 1;
for (int i = 1; i < n; i++)
{
for (int j = 0; j < i; j++)
{
if (arr[j] < arr[i] &&
Z[i][0] < Z[j][1] + 1)
Z[i][0] = Z[j][1] + 1;
if( arr[j] > arr[i] &&
Z[i][1] < Z[j][0] + 1)
Z[i][1] = Z[j][0] + 1;
}
if (res < Math.max(Z[i][0], Z[i][1]))
res = Math.max(Z[i][0], Z[i][1]);
}
return res;
}
public static void main(String[] args)
{
int arr[] = { 10, 22, 9, 33, 49,
50, 31, 60 };
int n = arr.length;
System.out.println("Length of Longest "+
"Zig-Zag subsequence is " +
zzis(arr, n));
}
}
|
Python3
def zzis(arr, n):
Z = [[1 for i in range(2)] for i in range(n)]
res = 1
for i in range(1, n):
for j in range(i):
if (arr[j] < arr[i] and Z[i][0] < Z[j][1] + 1):
Z[i][0] = Z[j][1] + 1
if( arr[j] > arr[i] and Z[i][1] < Z[j][0] + 1):
Z[i][1] = Z[j][0] + 1
if (res < max(Z[i][0], Z[i][1])):
res = max(Z[i][0], Z[i][1])
return res
arr = [10, 22, 9, 33, 49, 50, 31, 60]
n = len(arr)
print("Length of Longest Zig-Zag subsequence is",
zzis(arr, n))
|
C#
using System;
class GFG
{
static int zzis(int []arr, int n)
{
int [,]Z = new int[n, 2];
for (int i = 0; i < n; i++)
Z[i, 0] = Z[i, 1] = 1;
int res = 1;
for (int i = 1; i < n; i++)
{
for (int j = 0; j < i; j++)
{
if (arr[j] < arr[i] &&
Z[i, 0] < Z[j, 1] + 1)
Z[i, 0] = Z[j, 1] + 1;
if( arr[j] > arr[i] &&
Z[i, 1] < Z[j, 0] + 1)
Z[i, 1] = Z[j, 0] + 1;
}
if (res < Math.Max(Z[i, 0], Z[i, 1]))
res = Math.Max(Z[i, 0], Z[i, 1]);
}
return res;
}
static public void Main ()
{
int []arr = {10, 22, 9, 33,
49, 50, 31, 60};
int n = arr.Length;
Console.WriteLine("Length of Longest "+
"Zig-Zag subsequence is " +
zzis(arr, n));
}
}
|
PHP
<?php
function maxD($a, $b) {
return ($a > $b) ? $a : $b;
}
function zzis($arr, $n)
{
for ($i = 0; $i < $n; $i++)
$Z[$i][0] = $Z[$i][1] = 1;
$res = 1;
for ($i = 1; $i < $n; $i++)
{
for ($j = 0; $j < $i; $j++)
{
if ($arr[$j] < $arr[$i] && $Z[$i][0] < $Z[$j][1] + 1)
$Z[$i][0] = $Z[$j][1] + 1;
if( $arr[$j] > $arr[$i] && $Z[$i][1] < $Z[$j][0] + 1)
$Z[$i][1] = $Z[$j][0] + 1;
}
if ($res < max($Z[$i][0], $Z[$i][1]))
$res = max($Z[$i][0], $Z[$i][1]);
}
return $res;
}
$arr = array( 10, 22, 9, 33, 49, 50, 31, 60 );
$n = sizeof($arr);
echo "Length of Longest Zig-Zag subsequence is ",
zzis($arr, $n) ;
echo "\n";
#This code is contributed by aj_36
?>
|
Javascript
<script>
function zzis(arr, n)
{
let Z = new Array(n);
for(let i = 0; i < n; i++)
{
Z[i] = new Array(2);
}
for (let i = 0; i < n; i++)
Z[i][0] = Z[i][1] = 1;
let res = 1;
for (let i = 1; i < n; i++)
{
for (let j = 0; j < i; j++)
{
if (arr[j] < arr[i] &&
Z[i][0] < Z[j][1] + 1)
Z[i][0] = Z[j][1] + 1;
if( arr[j] > arr[i] &&
Z[i][1] < Z[j][0] + 1)
Z[i][1] = Z[j][0] + 1;
}
if (res < Math.max(Z[i][0], Z[i][1]))
res = Math.max(Z[i][0], Z[i][1]);
}
return res;
}
let arr = [ 10, 22, 9, 33, 49, 50, 31, 60 ];
let n = arr.length;
document.write("Length of Longest "+ "Zig-Zag subsequence is " + zzis(arr, n));
</script>
|
OutputLength of Longest Zig-Zag subsequence is 6
Time Complexity : O(n2)
Auxiliary Space : O(n)
A better approach with time complexity O(n) is explained below:
Let the sequence be stored in an unsorted integer array arr[N].
We shall proceed by comparing the mathematical signs(negative or positive) of the difference of two consecutive elements of arr. To achieve this, we shall store the sign of (arr[i] – arr[i-1]) in a variable, subsequently comparing it with that of (arr[i+1] – arr[i]). If it is different, we shall increment our result. For checking the sign, we shall use a simple Signum Function, which shall determine the sign of a number passed to it. That is,
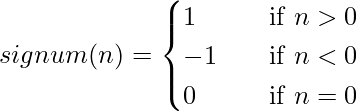
Considering the fact that we traverse the sequence only once, this becomes an O(n) solution.
The algorithm for the approach discussed above is :
Input integer array seq[N].
Initialize integer lastSign to 0.
FOR i in range 1 to N - 1
integer sign = signum(seq[i] - seq[i-1])
IF sign != lastSign AND IF sign != 0
increment length by 1. lastSign = sign.
END IF
END FOR
return length.
Following is the implementation of the above approach:
C++
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
int signum(int n);
int maxZigZag(int seq[], int n)
{
if (n == 0) {
return 0;
}
int lastSign = 0, length = 1;
for (int i = 1; i < n; ++i) {
int Sign = signum(seq[i] - seq[i - 1]);
if (Sign != lastSign && Sign != 0)
{
lastSign = Sign;
length++;
}
}
return length;
}
int signum(int n)
{
if (n != 0) {
return n > 0 ? 1 : -1;
}
else {
return 0;
}
}
int main()
{
int sequence1[4] = { 1, 3, 6, 2 };
int sequence2[5] = { 5, 0, 3, 1, 0 };
int n1 = sizeof(sequence1)
/ sizeof(*sequence1);
int n2 = sizeof(sequence2) / sizeof(*sequence2);
int maxLength1 = maxZigZag(sequence1, n1);
int maxLength2
= maxZigZag(sequence2, n2);
cout << "The maximum length of zig-zag sub-sequence in "
"first sequence is: "
<< maxLength1;
cout << endl;
cout << "The maximum length of zig-zag sub-sequence in "
"second sequence is: "
<< maxLength2;
}
|
Java
import java.util.*;
import java.io.*;
class zigZagMaxLength {
public static void main(String[] args)
{
int[] sequence1 = { 1, 3, 6, 2 };
int[] sequence2 = { 5, 0, 3, 1, 0 };
int n1 = sequence1.length;
int n2 = sequence2.length;
int maxLength1 = maxZigZag(sequence1, n1);
int maxLength2
= maxZigZag(sequence2, n2);
System.out.println(
"The maximum length of zig-zag sub-sequence in first sequence is: "
+ maxLength1);
System.out.println(
"The maximum length of zig-zag sub-sequence in second sequence is: "
+ maxLength2);
}
static int maxZigZag(int[] seq, int n)
{
if (n == 0) {
return 0;
}
int lastSign = 0, length = 1;
for (int i = 1; i < n; ++i) {
int Sign = signum(seq[i] - seq[i - 1]);
if (Sign != 0
&& Sign != lastSign)
{
lastSign = Sign;
length++;
}
}
return length;
}
static int signum(int n)
{
if (n != 0) {
return n > 0 ? 1 : -1;
}
else {
return 0;
}
}
}
|
Python3
def maxZigZag(seq, n):
if (n == 0):
return 0
lastSign = 0
length = 1
for i in range(1, n):
Sign = signum(seq[i] - seq[i - 1])
if (Sign != lastSign and Sign != 0):
lastSign = Sign
length += 1
return length
def signum(n):
if (n != 0):
return 1 if n > 0 else -1
else:
return 0
if __name__ == '__main__':
sequence1 = [1, 3, 6, 2]
sequence2 = [5, 0, 3, 1, 0]
n1 = len(sequence1)
n2 = len(sequence2)
maxLength1 = maxZigZag(sequence1, n1)
maxLength2 = maxZigZag(sequence2, n2)
print("The maximum length of zig-zag sub-sequence "
"in first sequence is:", maxLength1)
print("The maximum length of zig-zag sub-sequence "
"in second sequence is:", maxLength2)
|
C#
using System;
class zigZagMaxLength {
public static void Main(String[] args)
{
int[] sequence1 = { 1, 3, 6, 2 };
int[] sequence2 = { 5, 0, 3, 1, 0 };
int n1 = sequence1.Length;
int n2 = sequence2.Length;
int maxLength1 = maxZigZag(sequence1, n1);
int maxLength2
= maxZigZag(sequence2, n2);
Console.WriteLine(
"The maximum length of zig-zag sub-sequence"
+ " in first sequence is: " + maxLength1);
Console.WriteLine(
"The maximum length of zig-zag "
+ "sub-sequence in second sequence is: "
+ maxLength2);
}
static int maxZigZag(int[] seq, int n)
{
if (n == 0) {
return 0;
}
int lastSign = 0, length = 1;
for (int i = 1; i < n; ++i) {
int Sign = signum(seq[i] - seq[i - 1]);
if (Sign != 0
&& Sign != lastSign)
{
lastSign = Sign;
length++;
}
}
return length;
}
static int signum(int n)
{
if (n != 0) {
return n > 0 ? 1 : -1;
}
else {
return 0;
}
}
}
|
Javascript
<script>
function maxZigZag(seq, n)
{
if (n == 0) {
return 0;
}
let lastSign = 0, length = 1;
for (let i = 1; i < n; ++i) {
let Sign = signum(seq[i] - seq[i - 1]);
if (Sign != 0 && Sign != lastSign)
{
lastSign = Sign;
length++;
}
}
return length;
}
function signum(n)
{
if (n != 0) {
return n > 0 ? 1 : -1;
}
else {
return 0;
}
}
let sequence1 = [ 1, 3, 6, 2 ];
let sequence2 = [ 5, 0, 3, 1, 0 ];
let n1 = sequence1.length;
let n2 = sequence2.length;
let maxLength1 = maxZigZag(sequence1, n1);
let maxLength2 = maxZigZag(sequence2, n2);
document.write("The maximum length of zig-zag sub-sequence"
+ " in first sequence is: " + maxLength1 + "</br>");
document.write(
"The maximum length of zig-zag "
+ "sub-sequence in second sequence is: "
+ maxLength2 + "</br>");
</script>
|
OutputThe maximum length of zig-zag sub-sequence in first sequence is: 3
The maximum length of zig-zag sub-sequence in second sequence is: 4
Time Complexity : O(n)
Auxiliary Space : O(1)
Share your thoughts in the comments
Please Login to comment...