Lexicographically smallest array formed by at most one swap for every pair of adjacent indices
Last Updated :
28 Sep, 2022
Given an array A[] of length N, the task is to find lexicographically smallest array by swapping adjacent elements for each index atmost once. Thus, for any index:
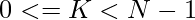
, at most one swap between A[K] and A[K+1] is allowed.
Example:
Input: A[] = { 3, 2, 1, 4}
Output: 1 3 2 4
Explanation: Perform the following swaps:
Swap A[1] and A[2], now A[] = { 3, 1, 2, 4 }
Swap A[0] and A[1], now A[] = { 1, 3, 2, 4 }
No further swaps are possible as A[1] and A[2] have already been swapped.
Input: A[] = { 2, 1, 4, 3, 6, 5 }
Output: 1 2 3 4 5 6
Explanation: Perform the following swaps:
Swap A[0] and A[1], now A[] = { 1, 2, 4, 3, 6, 5 }
Swap A[2] and A[3], now A[] = { 1, 2, 3, 4, 6, 5 }
Swap A[4] and A[5], now A[] = { 1, 2, 3, 4, 5, 6 }
Approach:
To solve the problem mentioned above we can apply Greedy method. We know that we can perform at most N – 1 swaps to make the given array as smallest as possible.
- Create a counter variable and initialize with N-1 and a hash-map to store performed swaps.
- Find the position of the minimum element from current index onward.
- Now perform swap backwards until we reach current element position.
- Also check if current swap is possible or not and decrement the counter also at each swap.
- Finally print the required array.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findSmallestArray(int A[], int n)
{
int count = n - 1;
map<pair<int, int>, int> mp;
for (int i = 0; i < n && count > 0; ++i) {
int mn = A[i], pos = i;
for (int j = i + 1; j < n; ++j) {
if (A[j] < mn) {
mn = A[j];
pos = j;
}
}
while (pos > i && count > 0
&& !mp[{ pos - 1, pos }]) {
mp[{ pos - 1, pos }] = 1;
swap(A[pos], A[pos - 1]);
--pos;
--count;
}
}
for (int i = 0; i < n; ++i)
cout << A[i] << " ";
}
int main()
{
int A[] = { 2, 1, 4, 3, 6, 5 };
int n = sizeof(A) / sizeof(A[0]);
findSmallestArray(A, n);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void findSmallestArray(int[] A, int n)
{
int count = n - 1;
HashMap<String, Integer> mp
= new HashMap<String, Integer>();
for (int i = 0; i < n && count > 0; ++i) {
int mn = A[i];
int pos = i;
for (int j = i + 1; j < n; ++j) {
if (A[j] < mn) {
mn = A[j];
pos = j;
}
}
while (pos > i && count > 0
&& !mp.containsKey(
String.valueOf(pos - 1) + "#"
+ String.valueOf(pos))) {
mp.put(String.valueOf(pos - 1) + "#"
+ String.valueOf(pos), 1);
var temp = A[pos];
A[pos] = A[pos - 1];
A[pos - 1] = temp;
--pos;
--count;
}
}
for (int i = 0; i < n; ++i)
System.out.print(A[i] + " ");
}
public static void main(String[] args)
{
int[] A = { 2, 1, 4, 3, 6, 5 };
int n = A.length;
findSmallestArray(A, n);
}
}
|
Python3
def findSmallestArray(A, n):
count = n - 1
mp = {''}
for i in range(0, n):
if(count <= 0):
break;
mn = A[i]
pos = i
for j in range(i + 1, n):
if (A[j] < mn):
mn = A[j]
pos = j
while (pos > i and count > 0 and
((pos - 1, pos) not in mp)):
mp.add((pos - 1, pos))
A[pos], A[pos - 1] = A[pos - 1], A[pos]
pos -= 1
count -= 1
for i in range(0, n):
print(A[i], end = " ")
A = [ 2, 1, 4, 3, 6, 5 ]
n = len(A)
findSmallestArray(A, n)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static void findSmallestArray(int[] A, int n)
{
int count = n - 1;
Dictionary<string, int> mp
= new Dictionary<string, int>();
for (int i = 0; i < n && count > 0; ++i) {
int mn = A[i];
int pos = i;
for (int j = i + 1; j < n; ++j) {
if (A[j] < mn) {
mn = A[j];
pos = j;
}
}
while (pos > i && count > 0
&& !mp.ContainsKey(
Convert.ToString(pos - 1) + "#"
+ Convert.ToString(pos))) {
mp[Convert.ToString(pos - 1) + "#"
+ Convert.ToString(pos)]
= 1;
var temp = A[pos];
A[pos] = A[pos - 1];
A[pos - 1] = temp;
--pos;
--count;
}
}
for (int i = 0; i < n; ++i)
Console.Write(A[i] + " ");
}
public static void Main(string[] args)
{
int[] A = { 2, 1, 4, 3, 6, 5 };
int n = A.Length;
findSmallestArray(A, n);
}
}
|
Javascript
function findSmallestArray(A, n)
{
let count = n - 1;
let mp = {};
for (var i = 0; i < n && count > 0; ++i) {
var mn = A[i], pos = i;
for (var j = i + 1; j < n; ++j) {
if (A[j] < mn) {
mn = A[j];
pos = j;
}
}
while (pos > i && count > 0
&& !mp.hasOwnProperty(pos - 1 + "#" + pos)) {
mp[ pos - 1 + "#" + pos] = 1;
var temp = A[pos];
A[pos] = A[pos - 1]
A[pos - 1] = temp
--pos;
--count;
}
}
console.log(A.join(" "))
}
let A = [ 2, 1, 4, 3, 6, 5 ];
let n = A.length;
findSmallestArray(A, n);
|
Time Complexity: O(N2)
Share your thoughts in the comments
Please Login to comment...