Levene’s test
Last Updated :
05 Jun, 2023
In this article, we will learn about Levene’s test which is generally used to assess the equality of variances between two or more groups or samples.
What is Levene Test?
Levene’s test is used to assess the equality of variance between two different samples. For every case, it calculates the absolute difference between the value of that case and its cell mean and performs a one-way analysis of variance (ANOVA) on those differences
Assumptions of Levene’s Test
- The samples from the populations under consideration are independent.
- The populations under consideration are approximately normally distributed.
How to Perform Levene’s Test?
The null hypothesis for Levene’s test is that the variance among groups is equal.
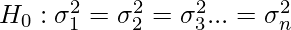
The alternative hypothesis is that the variance among different groups is not equal (for at least one pair the variance is not equal to others).
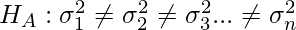
The test statistics for Levene’s test are:
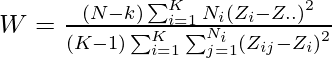
where,
- k: number of different groups to which the sampled cases belong.
- Ni: Number of elements in different groups.
- N: total number of cases in all groups
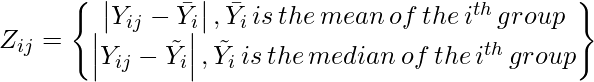
where,
- Yij: the value of the jth case and ith group.
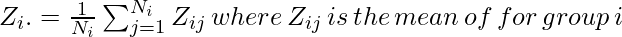
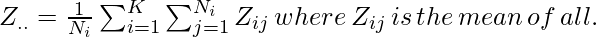
There are three types of Levene’s statistics available
- If a distribution has a longer-tailed distribution like the Cauchy distribution then we use a trimmed mean.
- For skewed distribution, if the distribution is not clear we will use the median for test statistics.
- For the symmetric distribution and moderately tailed distribution, we use mean value for distribution.
- Decide the level of significance (alpha). Generally, we take it as 0.05.
- Find the critical value in the F-distribution table for the given level of significance, (N-k), and (k-1) parameters.
- If W > F∝, k-1, N-k, then we reject the null hypothesis.
- else, we do not reject the null hypothesis.
Suppose there are 2 groups of students containing their scores in a maths test are below:
Group 1
| Group 2
|
|---|
14
| 34
|
34
| 36
|
16
| 44
|
43
| 18
|
45
| 42
|
36
| 39
|
42
| 16
|
43
| 35
|
16
| 15
|
27
| 33
|
Here, our null hypothesis is defined as:
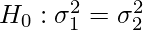
and the alternate hypothesis is
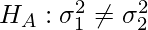
And our level of significance is:
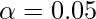
Now, calculate the test statistics using the above formula
| | Group 1
| Group 2
| G1 (Y) : (Xi – Mean)
| G2 (Z) : (Xi – Mean)
| (Yi– meanVar)2
| (Zi– meanVar)2
|
|---|
| | 14
| 34
| 2.8
| 17.6
| 49
| 60.84
|
| | 34
| 36
| 4.8
| 2.4
| 25
| 54.76
|
| | 16
| 44
| 12.8
| 15.6
| 9
| 33.64
|
| | 43
| 18
| 13.2
| 11.4
| 11.56
| 2.56
|
| | 45
| 42
| 10.8
| 13.4
| 1
| 12.96
|
| | 36
| 39
| 7.8
| 4.4
| 4
| 29.16
|
| | 42
| 16
| 15.2
| 10.4
| 29.16
| 0.36
|
| | 43
| 35
| 3.8
| 11.4
| 36
| 2.56
|
| | 16
| 15
| 16.2
| 15.6
| 40.96
| 33.64
|
| | 27
| 33
| 1.8
| 4.6
| 64
| 27.04
|
| Average | 31.6
| 31.2
| 8.92
| 10.68
|
|
|
where meanVar is,
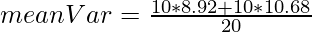
- and k – 1 = Num of groups -1 =1
- N – k = 20 – 2 = 18.
- By solving the test statistics using the following parameters
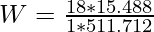
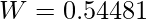
- Since, W < F0.05,1,19, hence we do not reject the null hypothesis.
Levene’s Test using Scipy
Now let’s look at the code implementation for Levene’s test using the Scipy package in Python which was dedicatedly built for complex mathematical computations in Python.
Python3
from scipy.stats import levene
group_1 = [14, 34, 16, 43, 45,
36, 42, 43, 16, 27]
group_2 = [34, 36, 44, 18, 42,
39, 16, 35, 15, 33]
alpha = 0.05
w_stats, p_value = levene(group_1, group_2,
center='mean')
if p_value > alpha:
print("We do not reject the null hypothesis")
else:
print("Reject the Null Hypothesis")
|
Output:
We do not reject the null hypothesis
Share your thoughts in the comments
Please Login to comment...