Larger of a^b or b^a (a raised to power b or b raised to power a)

Given two numbers 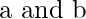, find which is greater .
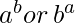If 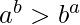, print a^b is greater 
If 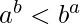, print b^a is greater 
If 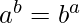, print Both are equal
Examples:

Input : 3 5
Output : a^b is greater
3^5 = 243, 5^3 = 125. Since, 243>125, therefore a^b > b^a.

Input : 2 4
Output : Both are equal
2^4 = 16, 4^2 = 16. Since, 16=16, therefore a^b = b^a.

Brute Force solution would be to just compute 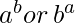and compare them. But since can be large enough that 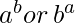can not be stored even in long long int, so this solution is not feasible. Also computing to the power n would require at least 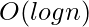time using the fast exponentiation technique.
Efficient approach would be to use logarithm. We have to compare 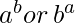. If we take log, the problem reduces to comparing . 
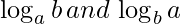Hence,
If 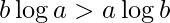, print a^b is greater 
If 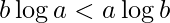, print b^a is greater 
If 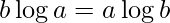, print Both are equal
Below is the implementation of the efficient approach discussed above. 

C++

// C++ code for finding greater
// between the a^b and b^a
#include <bits/stdc++.h>
using namespace std;

// Function to find the greater value
void findGreater(int a, int b)
{
    long double x = (long double)a * (long double)(log((long double)(b)));
    long double y = (long double)b * (long double)(log((long double)(a)));
    if (y > x) {
        cout << "a^b is greater" << endl;
    }
    else if (y < x) {
        cout << "b^a is greater" << endl;
    }
    else {
        cout << "Both are equal" << endl;
    }
}

// Driver code
int main()
{
    int a = 3, b = 5, c = 2, d = 4;
    findGreater(a, b);
    findGreater(c, d);
    return 0;
}

Java

// Java code for finding greater
// between the a^b and b^a

public class GFG{

    // Function to find the greater value
    static void findGreater(int a, int b)
    {
        double x = (double)a * (double)(Math.log((double)(b)));
        double y = (double)b * (double)(Math.log((double)(a)));
        if (y > x) {
            System.out.println("a^b is greater") ;
        }
        else if (y < x) {
            System.out.println("b^a is greater") ;
        }
        else {
            System.out.println("Both are equal") ;
        }
    }

    // Driver code
    public static void main(String []args)
    {
        int a = 3, b = 5, c = 2, d = 4;
        findGreater(a, b);
        findGreater(c, d);
    }
    // This code is contributed by Ryuga
}

Python 3

# Python 3 code for finding greater
# between the a^b and b^a
import math

# Function to find the greater value
def findGreater(a, b):

    x = a * (math.log(b));
    y = b * (math.log(a));
    if (y > x):
        print ("a^b is greater");
    elif (y < x):
        print("b^a is greater");
    else :
        print("Both are equal");

# Driver code
a = 3;
b = 5;
c = 2;
d = 4;
findGreater(a, b);
findGreater(c, d);

# This code is contributed
# by Shivi_Aggarwal

C#

// C# code for finding greater
// between the a^b and b^a

using System;
public class GFG{

    // Function to find the greater value
    static void findGreater(int a, int b)
    {
        double x = (double)a * (double)(Math.Log((double)(b)));
        double y = (double)b * (double)(Math.Log((double)(a)));
        if (y > x) {
            Console.Write("a^b is greater\n") ;
        }
        else if (y < x) {
            Console.Write("b^a is greater"+"\n") ;
        }
        else {
            Console.Write("Both are equal") ;
        }
    }

    // Driver code
    public static void Main()
    {
        int a = 3, b = 5, c = 2, d = 4;
        findGreater(a, b);
        findGreater(c, d);
    }

}

PHP

<?php
// PHP code for finding greater
// between the a^b and b^a

// Function to find the greater value
function findGreater($a, $b)
{
    $x = (double)$a * (double)(log((double)($b)));
    $y = (double)$b * (double)(log((double)($a)));
    if ($y > $x)
    {
        echo "a^b is greater", "\n";
    }
    else if ($y < $x)
    {
        echo "b^a is greater", "\n" ;
    }
    else
    {
        echo "Both are equal", "\n" ;
    }
}

// Driver code
$a = 3;
$b = 5;
$c = 2;
$d = 4;
findGreater($a, $b);
findGreater($c, $d);

// This code is contributed by ajit
?>

Javascript

<script>
// javascript code for finding greater
// between the a^b and b^a

    // Function to find the greater value
    function findGreater(a , b) {
        var x =  a * (Math.log( (b)));
        var y =  b * (Math.log( (a)));
        if (y > x) {
            document.write("a^b is greater<br/>");
        } else if (y < x) {
            document.write("b^a is greater<br/>");
        } else {
            document.write("Both are equal<br/>");
        }
    }

    // Driver code

        var a = 3, b = 5, c = 2, d = 4;
        findGreater(a, b);
        findGreater(c, d);

// This code is contributed by todaysgaurav
</script>

Output:

a^b is greater
Both are equal

Time Complexity: O(logn), since it is using inbuilt log function

Auxiliary Space: O(1), since no extra space has been taken.