Find parent of given node in a Binary Tree with given postorder traversal

Given two integers N and K where N denotes the height of a binary tree, the task is to find the parent of the node with value K in a binary tree whose postorder traversal is first 

natural numbers 

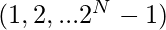
For N = 3, the Tree will be -

      7
    /   \
   3     6
 /   \  /  \
1     2 4   5

Examples:

Input: N = 4, K = 5 
Output: 6 
Explanation:
Parent of the node 5 is 6. As shown in the tree above.
Input: N = 5, K = 3 
Output: 7 
Explanation:
Parent of the node 3 is 7. As shown in the tree above. 

Naive Approach: A simple approach is to build the tree according to the following pattern and then traverse the whole tree to find the parent of a given node.
Efficient Approach: The idea is to use a binary search to find the parent of the node. As we know the binary Tree of Height N has 

nodes. Therefore, the search space for the binary search will be 1 to 

Now each node has children value either 

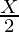
or 

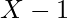
Therefore, parents of such nodes can be found easily.
Below is the implementation of the above approach:

C++

// C++ implementation to find the
// parent of the given node K in
// a binary tree whose post-order
// traversal is N natural numbers

#include <bits/stdc++.h>
using namespace std;

// Function to find the parent
// of the given node
int findParent(int height, int node)
{
    int start = 1;
    int end = pow(2, height) - 1;

    // Condition to check whether
    // the given node is a root node.
    // if it is then return -1 because
    // root node has no parent
    if (end == node)
        return -1;

    // Loop till we found
    // the given node
    while (node >= 1) {
        end = end - 1;

        // Finding the middle node of the
        // tree because at every level
        // tree parent is
        // divided into two halves
        int mid = start
                  + (end - start)
                        / 2;

        // if the node is found return
        // the parent always the child
        // nodes of every node
        // is node/2 or (node-1)
        if (mid == node || end == node) {
            return (end + 1);
        }

        // if the node to be found
        // is greater than the mid
        // search for left subtree else
        // search in right subtree
        else if (node < mid) {
            end = mid;
        }
        else {
            start = mid;
        }
    }
}

// Driver Code
int main()
{
    int height = 4;
    int node = 6;

    int k = findParent(height, node);
    cout << k;

    return 0;
}

Java

// Java implementation to find the
// parent of the given node K in
// a binary tree whose post-order
// traversal is N natural numbers
import java.util.*;
class GFG{

// Function to find the parent
// of the given node
static int findParent(int height,
                      int node)
{
  int start = 1;
  int end = (int)Math.pow(2, height) - 1;

  // Condition to check whether
  // the given node is a root node.
  // if it is then return -1 because
  // root node has no parent
  if (end == node)
    return -1;

  // Loop till we found
  // the given node
  while (node >= 1)
  {
    end = end - 1;

    // Finding the middle node of the
    // tree because at every level
    // tree parent is
    // divided into two halves
    int mid = start + (end - start) / 2;

    // if the node is found return
    // the parent always the child
    // nodes of every node
    // is node*/2 or (node-1)
    if (mid == node || end == node)
    {
      return (end + 1);
    }

    // if the node to be found
    // is greater than the mid
    // search for left subtree else
    // search in right subtree
    else if (node < mid)
    {
      end = mid;
    }
    else
    {
      start = mid;
    }
  }
  return -1;
}

// Driver Code
public static void main(String[] args)
{
  int height = 4;
  int node = 6;
  int k = findParent(height, node);
  System.out.print(k);
}
}

// This code is contributed by gauravrajput1

Python3

# Python implementation to find the
# parent of the given node

import math

# Function to find the parent
# of the given node
def findParent(height, node):

    start = 1
    end = pow(2, height) - 1

    # Check whether the given node
    # is a root node.if it is then
    # return -1 because root
    # node has no parent
    if (end == node):
        return -1

    # Loop till we found
    # the given node
    while(node >= 1):

        end = end - 1

        # Find the middle node of the
        # tree because at every level
        # tree parent is divided
        # into two halves
        mid = start + (end - start)//2

        # if the node is found
        # return the parent
        # always the child nodes of every
        # node is node / 2 or (node-1)
        if(mid == node or end == node):
            return (end + 1)

        # if the node to be found is greater
        # than the mid search for left
        # subtree else search in right subtree
        elif (node < mid):
            end = mid

        else:
            start = mid

# Driver code
if __name__ == "__main__":
    height = 4
    node = 6

    # Function Call
    k = findParent(height, node)
    print(k)

C#

// C# implementation to find the
// parent of the given node K in
// a binary tree whose post-order
// traversal is N natural numbers
using System;
class GFG{

// Function to find the parent
// of the given node
static int findParent(int height,
                      int node)
{
  int start = 1;
  int end = (int)Math.Pow(2, height) - 1;

  // Condition to check whether
  // the given node is a root node.
  // if it is then return -1 because
  // root node has no parent
  if (end == node)
    return -1;

  // Loop till we found
  // the given node
  while (node >= 1)
  {
    end = end - 1;

    // Finding the middle node of the
    // tree because at every level
    // tree parent is
    // divided into two halves
    int mid = start + (end - start) / 2;

    // if the node is found return
    // the parent always the child
    // nodes of every node
    // is node*/2 or (node-1)
    if (mid == node || end == node)
    {
      return (end + 1);
    }

    // if the node to be found
    // is greater than the mid
    // search for left subtree else
    // search in right subtree
    else if (node < mid)
    {
      end = mid;
    }
    else
    {
      start = mid;
    }
  }
  return -1;
}

// Driver Code
public static void Main(String[] args)
{
  int height = 4;
  int node = 6;
  int k = findParent(height, node);
  Console.Write(k);
}
}

// This code is contributed by Princi Singh

Javascript

<script>
    // Javascript implementation to find the
    // parent of the given node K in
    // a binary tree whose post-order
    // traversal is N natural numbers

    // Function to find the parent
    // of the given node
    function findParent(height, node)
    {
      let start = 1;
      let end = Math.pow(2, height) - 1;

      // Condition to check whether
      // the given node is a root node.
      // if it is then return -1 because
      // root node has no parent
      if (end == node)
        return -1;

      // Loop till we found
      // the given node
      while (node >= 1)
      {
        end = end - 1;

        // Finding the middle node of the
        // tree because at every level
        // tree parent is
        // divided into two halves
        let mid = start + parseInt((end - start) / 2, 10);

        // if the node is found return
        // the parent always the child
        // nodes of every node
        // is node*/2 or (node-1)
        if (mid == node || end == node)
        {
          return (end + 1);
        }

        // if the node to be found
        // is greater than the mid
        // search for left subtree else
        // search in right subtree
        else if (node < mid)
        {
          end = mid;
        }
        else
        {
          start = mid;
        }
      }
      return -1;
    }

    let height = 4;
    let node = 6;
    let k = findParent(height, node);
    document.write(k);

 // This code is contributed by divyeshrabadiya07.
</script>

Output:

7

Time complexity: O(log n) where n is no of nodes in binary tree

Auxiliary Space: O(1)