Introduction to Simulation Modeling in Python
Last Updated :
03 Mar, 2021
Simulation is imitating the operations which take place within a system to study its behavior. Analyzing and creating the model of a system to predict its performance is called simulation modeling.
Simulation mimics a real-life process to determine or predict the response of the entire system. This helps to understand the dependency of each part of the system, their relations, and interactions. The process of simulating in real life can be costly. Therefore, we build a model to solve costly and complex ideas efficiently. Building a simulation model in an institution or organization increases profit.
A model is a replica of an original/real thing. A model can be either deterministic or probabilistic. A deterministic model is a model which does not involve any randomness. For a given initial condition you always get the same final condition.
A probabilistic model includes the randomness of elements. For example: tossing a coin, can be either heads or tails.
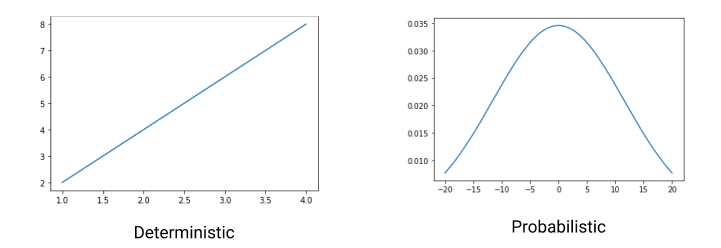
Now let’s understand the simulation model in one go.
Suppose you have to open a pizza restaurant and know how many employees you will need to run well. Different pizzas take different amounts of time to get prepared. Also, orders do not come uniformly with time. You want to provide them the best service possible while maintaining your budget. You can’t hire and then fire the employees to find the optimum number required to design a simulation model. We can solve the above problem of finding an optimum number of employees by building a simulation model in the following ways:
- Designing: looking over the various services provided by the company and, therefore, different types of employees required for various jobs.
- Experiment: Trends of customers’ arrival on weekdays, weekends, and on special occasions and therefore employees required accordingly.
- Optimize: Optimizing the number of workers to employ permanently by looking over experimentation.
- Analyze: If giving employment to those many people affordable or asking employees to work overtime, can get extra workers on festival season.
- Improve: Further reducing the employment to given on visualizing the results of the analysis.
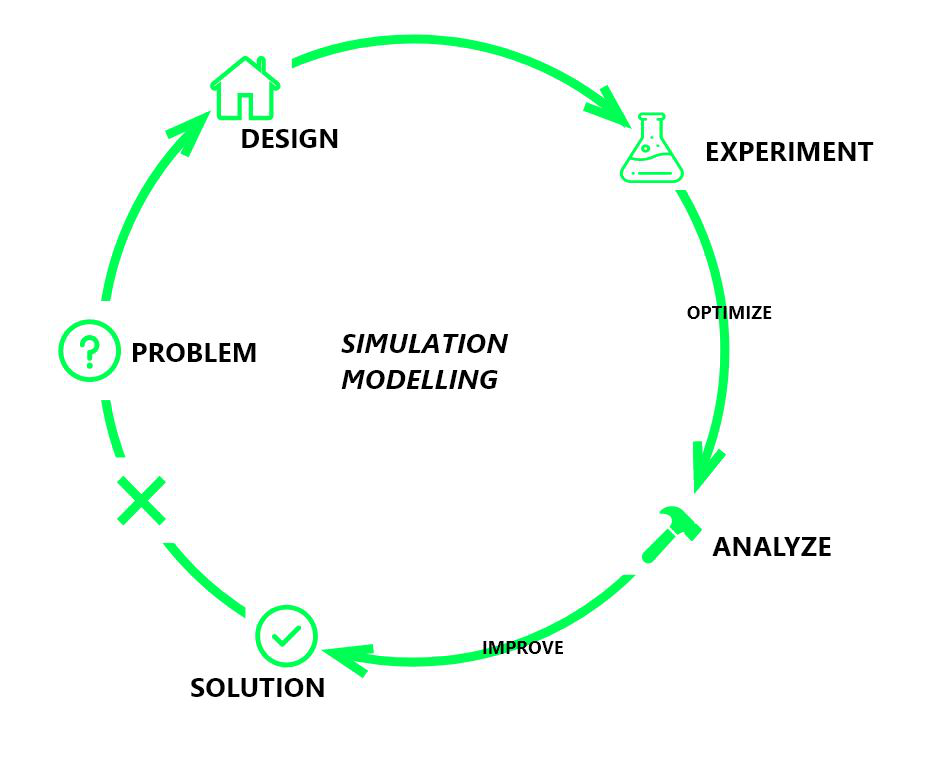
Simulation models are built before building a new system or altering an existing system to optimize the system’s performance and reduce the chances of failure. One of the leading simulation models in the present-day scenario is Monte Carlo Simulation.
Monte Carlo Simulation
Monte Carlo simulation is a mathematical technique that helps estimate the probability distribution of various event outcomes. Based on those probabilities, the risk analysis team decides whether they are ready to take the risk. This technique repeatedly takes random numbers between the minimum and maximum limit and predicts its outcome. Usually, the sampling is done on a large scale, so we get all the likely outcomes. Then we plot the probability distribution using which risk analysts calculate the risk probability.
For example, let’s consider the above example the arrival of customers can vary in a specific range. We can create a model that pics a random number between maximum and minimum number and can visualize the range of workers required accordingly.
Let’s take another elementary example to understand the Monte Carlo simulation by rolling the dice. Suppose we roll two dice, and we want to predict the probability of getting the sum as 12.
Below is the python code for the implementation with comments for better understanding:
Python3
import random
import numpy as np
import matplotlib.pyplot as plt
def roll():
return random.randint(1, 6)
val = []
for i in range(0, 1000000):
sum_of_roll = roll()+roll()
val.append(sum_of_roll)
plt.hist(val, bins=11, density=True)
|
Output:
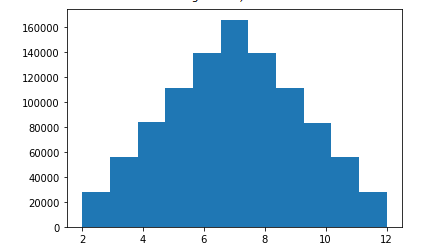
From the above probability distribution curve, we get the value of probability as 0.025 for getting a 12. Similarly, we can apply the Monte Carlo technique to solve various problems.
Share your thoughts in the comments
Please Login to comment...