Intersection of Sets

Intersection of Sets is the operation in set theory and is applied between two or more sets. It result in the output as all the elements which are common in all the sets under consideration. For example, The  intersection of sets A and B is the set of all elements which are common to both A and B.

Intersection of Sets

In other words, it is an operation that selects the common identical element among the sets. For example

Suppose, Set A is the set of odd Numbers less than 10 and Set B is the set of first 5 multiple of 3.

⇒ A = {1,3,5, 7,9}
⇒ B = {3,6,9,12,15}

So the common element in these two set are 3 and 9.

Hence, the set of intersection of A and B = {3,9}

Intersection of Sets

Intersection of Sets is defined as the set of common elements of all the sets. If A and B are two sets, then the intersection of set A and set B is the set of the same elements in both A and B. The intersection of sets is equivalent to logical AND. The intersection of two sets A and B is written as A ∩ B. If A = {p, q, r, s}, B = {r, s, t} then A ∩ B is,

A ∩ B = {r, s}

Here, the intersection of the set contains the common value in both sets.

Intersection of Sets Symbol

The intersection of sets is represented by the symbol ∩. The intersection of n sets can be written as Set 1 ∩ Set 2 ∩ …….. ∩ Set n.

Note: The result of the intersection of sets can be a set with no elements i.e., an empty set, if there is no common element in the sets under consideration.

How to Find Intersection of Sets

To find the intersection of the set, we can use the following steps:

Step 1: Compare the elements of the given sets.

Step 2: Select the common elements between both sets.

Step 3: Add the selected elements in the resultant set.

Step 4: Repeat above steps for all the given sets.

Step 5: The resultant set obtained represents intersection of sets.

A Intersection B Formula

From the above discussion, we know that A ∩ B set contains the common elements of sets A and B. There are several formulas related to the intersection of sets. On the basis of the cardinality of sets, the formula for finding a number of elements in the intersection of sets is given below:

Number of Elements in A Intersection B

If the cardinalities of sets A, B, and A ∪ B are given, then we can compute the cardinality of A ∩ B. Based on the cardinality (total number of elements in the set) the formula for finding the cardinality of the intersection of two sets is given by:

n(A ∩ B) = n(A) + n(B) – n(A ∪ B)

Where,

• n(A) is cardinality of set A,
• n(B) is cardinality of set B,
• n(A ∪ B) is cardinality of set A ∪ B, and
• n(A ∩ B) is cardinality of set A ∩ B.

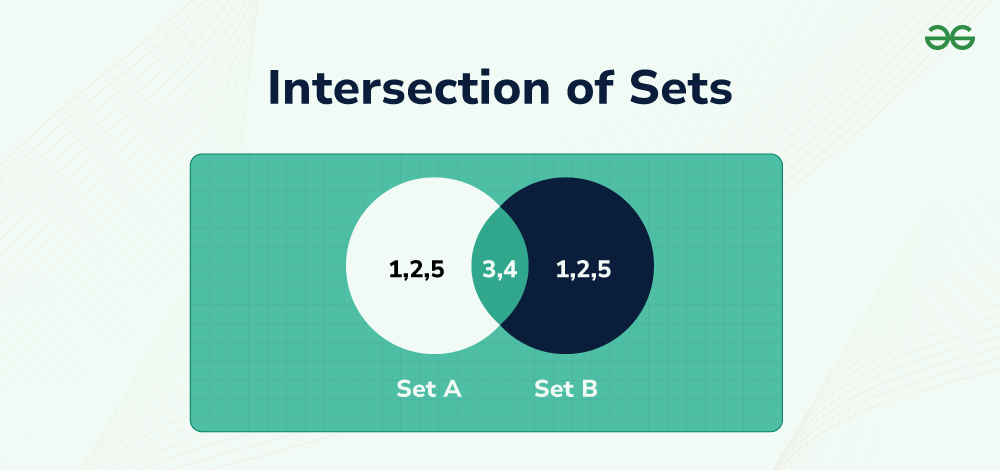
Venn Diagram of Intersection of Sets

Venn Diagram is a way of representing the sets and their interaction in a very effective visual way. Let’s consider the two cases of the intersection of two and three sets.

Intersection of Two Sets

Let A and B be two sets with some common elements. The resultant set for A ∩ B contains the common elements in both sets. Below is the Venn diagram for the intersection of two sets A and B.

Example: If A = {1, 6, 8} and B = {5, 8} then find A ∩ B.

Solution:

A = {1, 6, 8}

B = {5, 8}

A ∩ B = {1, 6, 8} ∩ {5, 8}

⇒ A ∩ B = {8}

Following is the Venn diagram for the intersection of two sets A and B.

Intersection of Sets Definition

If P and Q are two sets. The intersection of sets expressed in set builder form:

P ∩ Q = {x: x ∈ P and x ∈ Q}

⇒x ∈ (P ∩ Q) if and only if x ∈ P and x ∈ Q

Intersection of Three Sets

Intersection of sets can be performed among n number of sets. Let A, B, and C are three sets then, the intersection of these sets is the set of common elements in all the three sets. It is denoted by A ∩ B ∩ C.

Example: If P = {6, 7, 10}, Q = {7, 9, 12}, R = {7,15} then find P ∩ Q ∩ R.

Solution:

P = {6, 7, 10}, 

Q = {7, 9, 12}, and

R = {7,15}.

P ∩ Q ∩ R = {6, 7, 10} ∩ {7, 9, 12} ∩ {7, 15}

⇒ P ∩ Q ∩ R = {7}

Following is the Venn diagram for the intersection of three sets A, B, and C.

Properties of Intersection of Sets

Different properties of the Intersection of Sets are:

• Commutative Law
• Associative Law
• Distributive Law
• Law of Empty Set (ϕ)
• Law of Universal Set (U)
• Idempotent Law

Let’s discuss the above properties in detail. Consider three sets A, B, and C.

Commutative Law for Intersection

The commutative law of the intersection of sets states that the ordering of sets does not matter while performing an intersection.

A ∩ B = B ∩ A

Example: If A = {1, 10, 24, 31} and B = {1, 7,10, 24}. Verify commutative law.

Solution:

Given:

A = {1, 10, 24, 31}

B = {1, 7,10, 24}

A ∩ B = {1, 10, 24, 31} ∩ {1, 7,16, 24}

⇒ A ∩ B = {1, 24} —–(I)

B ∩ A = {1, 7,16, 24} ∩ {1, 10, 24, 31}

⇒ B ∩ A = {1, 24} —–(II)

From (I) and (II)

A ∩ B = B ∩ A [Hence Verified]

Associative Law for Intersection

The associative law of the intersection of sets states that we can perform the intersection of any two sets first in any order and then after other sets.

(A ∩ B) ∩ C = A ∩ (B ∩ C)

Example: If P = {2, 7, 15}, Q = {2, 9, 13}, R = {2, 23} then verify associative law.

Solution:

Given:

P = {2, 7, 15}, Q = {2, 9, 13}, R = {2, 23}

(P ∩ Q) ∩ R = [{2, 7, 15} ∩ {2, 9, 13}] ∩ {2, 23}

⇒ (P ∩ Q) ∩ R = {2} ∩ {2, 23}

⇒ (P ∩ Q) ∩ R = {2} ———(I)

Now,

P ∩ (Q ∩ R) = {2, 7, 15} ∩ [{2, 9, 13} ∩ {2, 23}]

⇒ P ∩ (Q ∩ R) = {2, 7, 15} ∩ {2}

⇒ P ∩ (Q ∩ R) = {2} ———(II)

From (I) and (II)

(P ∩ Q) ∩ R = P ∩ (Q ∩ R) [Hence Verified]

Distributive Law for Intersection

The distributive law of the intersection of sets states that the intersection of a set A with the union of the other two sets B and C is equivalent to the intersection of set A and B union intersection of set A and C.

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

Example: If P = {a, b, d}, Q = {b, c, d}, R = {b, d, j} then verify associative law.

Solution:

Given:

P = {a, b, d}, Q = {b, c, d}, R = {b, d, j}

⇒ (P ∩ Q) = {a, b, d} ∩ {b, c, d} = {b, d}

⇒ (P ∩ R) = {a, b, d} ∩ {b, d, j} = {b, d}

(Q ∪ R) = {b, c, d} ∪ {b, d, j} = {b, c, d, j}

⇒ P ∩ (Q ∪ R) = {a, b, d} ∩ {b, c, d, j}

⇒ P ∩ (Q ∪ R) = {b, d} ———(I)

Now,

(P ∩ Q) ∪ (P ∩ R) = {b, d} ∪ {b, d}

⇒ (P ∩ Q) ∪ (P ∩ R) = {b, d} ———(II)

From (I) and (II)

P ∩ (Q ∪ R) = (P ∩ Q) ∪ (P ∩ R) [Hence Verified]

Law of Empty set (ϕ) for Intersection

Law of empty set ϕ states that the intersection of an empty set with any other set results in the empty set.

A ∩ ϕ = ϕ

Example: If A = {1, 32} then verify the law of the Empty set.

Solution:

Given,

A = {1, 32}

⇒ A ∩ ϕ = {1, 32} ∩ { }

⇒ A ∩ ϕ = { }

Thus, A ∩ ϕ = ϕ [Hence Verified] 

Law of Universal set (U) for Intersection

Law of Universal set U states that the intersection of a universal set with any set results in the same set.

A ∩ U = A

Example: If A = {10, 12} and U = {10, 12, 14, 16} then verify the law of the Universal set.

Solution:

Given,

A = {10, 12} and U = {10, 12, 14, 16}

⇒ A ∩ U = {10, 12} ∩ {10, 12, 14, 16}

⇒ A ∩ U = {10, 12}

Thus, A ∩ U = A [Hence Verified]

Idempotent Law

Idempotent law states that the intersection of two same sets results in the same set.

A ∩ A = A

Example: If A = {5, 20} then verify Idempotent law.

Solution:

Given, A = {5, 20}

A ∩ A = {5, 20} ∩ {5, 20}

⇒ A ∩ A = {5, 20}

⇒ A ∩ A = A [Hence Verified]

Union and Intersection of Sets

Below is the difference between the union and intersection of sets are given as follows:

Characteristics	Union of Sets	Intersection of Sets
Definition	The union of sets is a set of all the distinct elements of the sets.	The intersection of sets is a set of all identical elements among sets.
Symbol	It is denoted by the symbol ∪.	It is denoted by the symbol ∩.
Written as	It is written as A ∪ B.	It is written as A ∩ B.
Equivalent Logic	It is equivalent to logical OR.	It is equivalent to logical AND.
Set Builder Form	P ∪ Q = {x: x ∈ P or x ∈ Q}	P ∩ Q = {x: x ∈ P and x ∈ Q}
Example	A = {2, 3}, B = {3, 4} Thus, A ∪ B = {2, 3, 4}	A = {2, 3}, B = {3, 4} Thus, A ∩ B = {3}

Read More

• Types of Set
  
• Union of Sets

Intersection of Sets Examples

Example 1: If A = {5, 6, 10, 13, 24} and B = {6, 7,11, 24}. Find (A ∩ B).

Solution:

Given:

A = {5, 6, 10, 13, 24}

B = {6, 7,11, 24}

To find: (A ∩ B)

A ∩ B = {5, 6, 10, 13, 24} ∩ {6, 7,11, 24}

⇒ A ∩ B = {6, 24}

Example 2: If P = {2, 5, 9}, Q = {2, 9, 10}, R = {2, 3, 9} then find P ∩ Q ∩ R.

Solution:

Given:

P = {2, 5, 9}

Q = {2, 9, 10}

R = {2, 3, 9}

To find: P ∩ Q ∩ R

P ∩ Q ∩ R = {2, 5, 9} ∩ {2, 9, 10} ∩ {2, 3, 9}

⇒ P ∩ Q ∩ R = {2, 9}

Example 3: Given the cardinalities of A, B, and A ∪ B as 6, 5 and 9 respectively. Find the cardinality of (A ∩ B).

Solution:

Given cardinalities of A, B and A ∪ B:

n(A) = 6

n(B) = 5

n(A ∪ B) = 9

n(A ∩ B) = n(A) + n(B) – n(A∪ B)

⇒ n(A ∩ B) = 6 + 5 – 9

⇒ n(A ∩ B) = 11 – 9

⇒ n(A ∩ B) = 2

The cardinality of (A ∩ B) = 2

Example 4: If X = {4, 5, 8}, Y = {1, 5, 9} and Universal set U = {1, 2, 3, 4, 5, 6, 8, 9}. Find (X ∩ Y)’

Solution:

Given

X = {4, 5, 8}

Y = {1, 5, 9}

X ∩ Y = {4, 5, 8} ∩ {1, 5, 9}

⇒ X ∩ Y = {5}

Thus, (X ∩ Y)’ = U – (X ∩ Y)

⇒ (X ∩ Y)’ = {1, 2, 3, 4, 5, 6, 8, 9} – {5}

⇒ (X ∩ Y)’ = {1, 2, 3, 4, 6, 8, 9}

Intersection of Sets – FAQs

Define the Intersection of Sets.

Intersection of Sets is the set of common elements in all the sets. It is denoted by symbol ∩.

Write the Set Builder form of the Intersection of Sets.

The set builder form of the intersection of sets:

P ∩ Q = {x: x ∈ P and x ∈ Q}

Where P and Q are two sets.

Mention the Properties of the Intersection of Sets.

The properties of intersection of sets are:

• Commutative Law
• Associative Law
• Distributive Law
• Law of Empty set ϕ and Universal set U
• Idempotent Law

What is the formula for finding the Cardinality of the Intersection of Sets?

The formula for finding cardinality intersection of sets is given by:

n(A∩B) = n(A) + n(B) – n(A∪ B)

Where,

• n(A) is cardinality of set A
• n(B) is cardinality of set B
• n(A ∪ B) is cardinality of set A ∪ B
• n(A ∩ B) is cardinality of set A ∩ B