Inclusion-Exclusion and its various Applications
Last Updated :
18 Apr, 2023
In the field of Combinatorics, it is a counting method used to compute the cardinality of the union set. According to basic Inclusion-Exclusion principle:
- For 2 finite sets
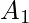 and
and 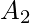 , which are subsets of Universal set, then
, which are subsets of Universal set, then 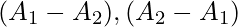 and
and  are disjoint sets.
are disjoint sets.
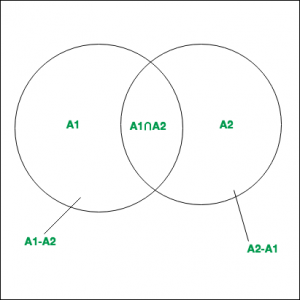
Hence it can be said that,
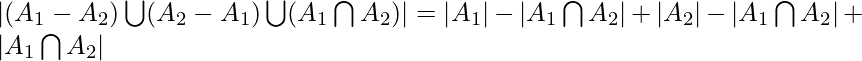
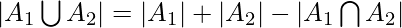 .
.- Similarly for 3 finite sets
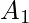 ,
, 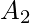 and
and 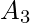 ,
,
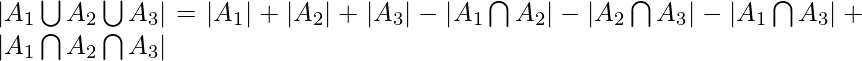
Principle :
Inclusion-Exclusion principle says that for any number of finite sets 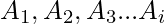 , Union of the sets is given by = Sum of sizes of all single sets – Sum of all 2-set intersections + Sum of all the 3-set intersections – Sum of all 4-set intersections .. +
, Union of the sets is given by = Sum of sizes of all single sets – Sum of all 2-set intersections + Sum of all the 3-set intersections – Sum of all 4-set intersections .. + 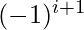 Sum of all the i-set intersections.
Sum of all the i-set intersections.
In general it can be said that,
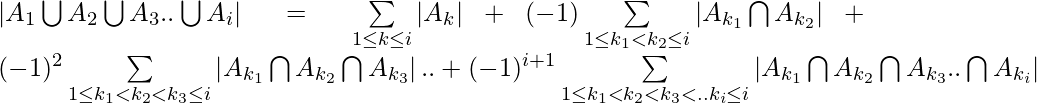
Properties :
- Computes the total number of elements that satisfy at least one of several properties.
- It prevents the problem of double counting.
Example 1:
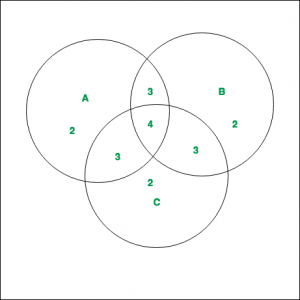
As shown in the diagram, 3 finite sets A, B and C with their corresponding values are given. Compute 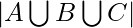 .
.
Solution :
The values of the corresponding regions, as can be noted from the diagram are –
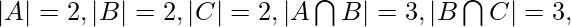
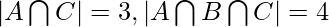
By applying Inclusion-Exclusion principle,
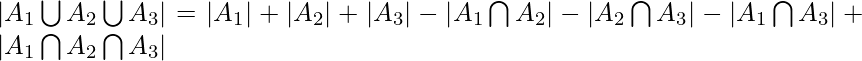
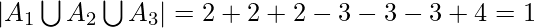
Applications :
- Derangements
To determine the number of derangements( or permutations) of n objects such that no object is in its original position (like Hat-check problem).
As an example we can consider the derangements of the number in the following cases:
For i = 1, the total number of derangements is 0.
For i = 2, the total number of derangements is 1. This is  .
.
For i = 3, the total number of derangements is 2. These are 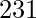 and 3 1 2.
and 3 1 2.
Approach : – Inclusion-Exclusion Principle is a combinatorial counting technique that allows us to count the number of elements in the union of multiple sets. The principle states that the size of the union of two or more sets is equal to the sum of their sizes minus the size of their intersection, plus the size of the intersection of their pairwise intersections, and so on.
Here’s the step-by-step approach in C++ to implement the Inclusion-Exclusion Principle:
Define the sets that need to be combined.
Compute the size of each set.
Compute the size of each intersection of two sets.
Compute the size of each intersection of three sets.
Continue computing the size of each intersection of four, five, and so on sets until you reach the final intersection.
Sum the sizes of all sets.
Subtract the size of all pairwise intersections.
Add the size of all three-way intersections.
Continue adding and subtracting the intersections of increasing sizes until you reach the final intersection.
Return the final count.
Here is an example of implementing the Inclusion-Exclusion Principle in C++ to find the number of positive integers less than 100 that are divisible by either 2, 3, or 5:
C++
#include <iostream>
using namespace std;
int main() {
int n = 100;
int count = 0;
for(int i = 2; i < n; i += 2) {
count++;
}
for(int i = 3; i < n; i += 3) {
count++;
}
for(int i = 5; i < n; i += 5) {
count++;
}
for(int i = 6; i < n; i += 6) {
count--;
}
for(int i = 10; i < n; i += 10) {
count--;
}
for(int i = 15; i < n; i += 15) {
count--;
}
for(int i = 30; i < n; i += 30) {
count++;
}
cout << "The number of positive integers less than " << n << " that are divisible by either 2, 3, or 5 is " << count << "." << endl;
return 0;
}
|
Python3
n = 100
count = 0
for i in range(2, n, 2):
count += 1
for i in range(3, n, 3):
count += 1
for i in range(5, n, 5):
count += 1
for i in range(6, n, 6):
count -= 1
for i in range(10, n, 10):
count -= 1
for i in range(15, n, 15):
count -= 1
for i in range(30, n, 30):
count += 1
print(f"The number of positive integers less than {n} that are divisible by either 2, 3, or 5 is {count}.")
|
Java
public class Main {
public static void main(String[] args) {
int n = 100;
int count = 0;
for (int i = 2; i < n; i += 2) {
count++;
}
for (int i = 3; i < n; i += 3) {
count++;
}
for (int i = 5; i < n; i += 5) {
count++;
}
for (int i = 6; i < n; i += 6) {
count--;
}
for (int i = 10; i < n; i += 10) {
count--;
}
for (int i = 15; i < n; i += 15) {
count--;
}
for (int i = 30; i < n; i += 30) {
count++;
}
System.out.println("The number of positive integers less than " + n + " that are divisible by either 2, 3, or 5 is " + count + ".");
}
}
|
OutputThe number of positive integers less than 100 that are divisible by either 2, 3, or 5 is 73.
Time complexity :- O(2^n) or O(n^k)
Auxiliary Space :- O(n log log n)
Share your thoughts in the comments
Please Login to comment...