Open In App

Implementing own Hash Table with Open Addressing Linear Probing

Last Updated : 25 Apr, 2024
Improve
Improve
Like Article
Like
Save
Share
Report

Prerequisite – Hashing Introduction, Implementing our Own Hash Table with Separate Chaining in Java
In Open Addressing, all elements are stored in the hash table itself. So at any point, size of table must be greater than or equal to total number of keys (Note that we can increase table size by copying old data if needed).

  • Insert(k) – Keep probing until an empty slot is found. Once an empty slot is found, insert k.
  • Search(k) – Keep probing until slot’s key doesn’t become equal to k or an empty slot is reached.
  • Delete(k) – Delete operation is interesting. If we simply delete a key, then search may fail. So slots of deleted keys are marked specially as “deleted”.

Here, to mark a node deleted we have used dummy node with key and value -1. 
Insert can insert an item in a deleted slot, but search doesn’t stop at a deleted slot.
The entire process ensures that for any key, we get an integer position within the size of the Hash Table to insert the corresponding value. 
So the process is simple, user gives a (key, value) pair set as input and based on the value generated by hash function an index is generated to where the value corresponding to the particular key is stored. So whenever we need to fetch a value corresponding to a key that is just O(1).
 

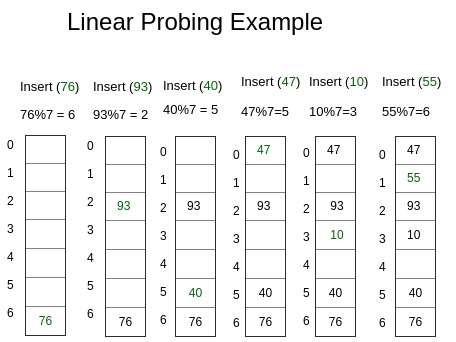
Implementation:

CPP 
#include <bits/stdc++.h>
using namespace std;

// template for generic type
template <typename K, typename V>

// Hashnode class
class HashNode {
public:
    V value;
    K key;

    // Constructor of hashnode
    HashNode(K key, V value)
    {
        this->value = value;
        this->key = key;
    }
};

// template for generic type
template <typename K, typename V>

// Our own Hashmap class
class HashMap {
    // hash element array
    HashNode<K, V>** arr;
    int capacity;
    // current size
    int size;
    // dummy node
    HashNode<K, V>* dummy;

public:
    HashMap()
    {
        // Initial capacity of hash array
        capacity = 20;
        size = 0;
        arr = new HashNode<K, V>*[capacity];

        // Initialise all elements of array as NULL
        for (int i = 0; i < capacity; i++)
            arr[i] = NULL;

        // dummy node with value and key -1
        dummy = new HashNode<K, V>(-1, -1);
    }
    // This implements hash function to find index
    // for a key
    int hashCode(K key) { return key % capacity; }

    // Function to add key value pair
    void insertNode(K key, V value)
    {
        HashNode<K, V>* temp
            = new HashNode<K, V>(key, value);

        // Apply hash function to find index for given key
        int hashIndex = hashCode(key);

        // find next free space
        while (arr[hashIndex] != NULL
               && arr[hashIndex]->key != key
               && arr[hashIndex]->key != -1) {
            hashIndex++;
            hashIndex %= capacity;
        }

        // if new node to be inserted
        // increase the current size
        if (arr[hashIndex] == NULL
            || arr[hashIndex]->key == -1)
            size++;
        arr[hashIndex] = temp;
    }

    // Function to delete a key value pair
    V deleteNode(int key)
    {
        // Apply hash function
        // to find index for given key
        int hashIndex = hashCode(key);

        // finding the node with given key
        while (arr[hashIndex] != NULL) {
            // if node found
            if (arr[hashIndex]->key == key) {
                HashNode<K, V>* temp = arr[hashIndex];

                // Insert dummy node here for further use
                arr[hashIndex] = dummy;

                // Reduce size
                size--;
                return temp->value;
            }
            hashIndex++;
            hashIndex %= capacity;
        }

        // If not found return null
        return NULL;
    }

    // Function to search the value for a given key
    V get(int key)
    {
        // Apply hash function to find index for given key
        int hashIndex = hashCode(key);
        int counter = 0;

        // finding the node with given key
        while (arr[hashIndex]
               != NULL) { // int counter =0; // BUG!

            if (counter++
                > capacity) // to avoid infinite loop
                return NULL;

            // if node found return its value
            if (arr[hashIndex]->key == key)
                return arr[hashIndex]->value;
            hashIndex++;
            hashIndex %= capacity;
        }

        // If not found return null
        return NULL;
    }

    // Return current size
    int sizeofMap() { return size; }

    // Return true if size is 0
    bool isEmpty() { return size == 0; }

    // Function to display the stored key value pairs
    void display()
    {
        for (int i = 0; i < capacity; i++) {
            if (arr[i] != NULL && arr[i]->key != -1)
                cout << "key = " << arr[i]->key
                     << "  value = " << arr[i]->value
                     << endl;
        }
    }
};

// Driver method to test map class
int main()
{
    HashMap<int, int>* h = new HashMap<int, int>;
    h->insertNode(1, 1);
    h->insertNode(2, 2);
    h->insertNode(2, 3);
    h->display();
    cout << h->sizeofMap() << endl;
    cout << h->deleteNode(2) << endl;
    cout << h->sizeofMap() << endl;
    cout << h->isEmpty() << endl;
    cout << h->get(2);

    return 0;
}
Java 
// Our own HashNode class
class HashNode {
    int key;
    int value;

    public HashNode(int key, int value)
    {
        this.key = key;
        this.value = value;
    }
}

// Our own Hashmap class
class HashMap {
    // hash element array
    int capacity;
    int size;
    HashNode[] arr;
    // dummy node
    HashNode dummy;

    public HashMap()
    {
        this.capacity = 20;
        this.size = 0;
        this.arr = new HashNode[this.capacity];
        // initialize with dummy node
        this.dummy = new HashNode(-1, -1);
    }

    // This implements hash function to find index for a key
    public int hashCode(int key)
    {
        return key % this.capacity;
    }

    // Function to add key value pair
    public void insertNode(int key, int value)
    {
        HashNode temp = new HashNode(key, value);
        // Apply hash function to find index for given key
        int hashIndex = hashCode(key);
        // find next free space
        while (this.arr[hashIndex] != null
               && this.arr[hashIndex].key != key
               && this.arr[hashIndex].key != -1) {
            hashIndex++;
            hashIndex %= this.capacity;
        }
        // if new node to be inserted, increase the current
        // size
        if (this.arr[hashIndex] == null
            || this.arr[hashIndex].key == -1) {
            this.size++;
        }
        this.arr[hashIndex] = temp;
    }

    // Function to delete a key value pair
    public int deleteNode(int key)
    {
        // Apply hash function to find index for given key
        int hashIndex = hashCode(key);
        // finding the node with given key
        while (this.arr[hashIndex] != null) {
            // if node found
            if (this.arr[hashIndex].key == key) {
                HashNode temp = this.arr[hashIndex];
                // Insert dummy node here for further use
                this.arr[hashIndex] = this.dummy;
                // Reduce size
                this.size--;
                return temp.value;
            }
            hashIndex++;
            hashIndex %= this.capacity;
        }
        // If not found return -1
        return -1;
    }

    // Function to search the value for a given key
    public int get(int key)
    {
        // Apply hash function to find index for given key
        int hashIndex = hashCode(key);
        int counter = 0;
        // finding the node with given key
        while (this.arr[hashIndex] != null) {
            // If counter is greater than capacity to avoid
            // infinite loop
            if (counter > this.capacity) {
                return -1;
            }
            // if node found return its value
            if (this.arr[hashIndex].key == key) {
                return this.arr[hashIndex].value;
            }
            hashIndex++;
            hashIndex %= this.capacity;
            counter++;
        }
        // If not found return 0
        return 0;
    }

    // Return current size
    public int sizeofMap() { return this.size; }

    // Return true if size is 0
    public boolean isEmpty() { return this.size == 0; }

    // Function to display the stored key value pairs
    public void display()
    {
        for (int i = 0; i < this.capacity; i++) {
            if (this.arr[i] != null
                && this.arr[i].key != -1) {
                System.out.println(
                    "key = " + this.arr[i].key
                    + " value = " + this.arr[i].value);
            }
        }
    }
}

public class Main {
    public static void main(String[] args)
    {
        HashMap h = new HashMap();
        h.insertNode(1, 1);
        h.insertNode(2, 2);
        h.insertNode(2, 3);
        h.display();
        System.out.println(h.sizeofMap());
        System.out.println(h.deleteNode(2));
        System.out.println(h.sizeofMap());
        System.out.println(h.isEmpty());
        System.out.println(h.get(2));
    }
}
Python3 
# Our own Hashnode class
class HashNode:
    def __init__(self, key, value):
        self.key = key
        self.value = value

# Our own Hashmap class


class HashMap:
    # hash element array
    def __init__(self):
        self.capacity = 20
        self.size = 0
        self.arr = [None] * self.capacity
        # dummy node
        self.dummy = HashNode(-1, -1)

    # This implements hash function to find index for a key
    def hashCode(self, key):
        return key % self.capacity

    # Function to add key value pair
    def insertNode(self, key, value):
        temp = HashNode(key, value)
        # Apply hash function to find index for given key
        hashIndex = self.hashCode(key)
        # find next free space
        while self.arr[hashIndex] is not None and self.arr[hashIndex].key != key and self.arr[hashIndex].key != -1:
            hashIndex += 1
            hashIndex %= self.capacity
        # if new node to be inserted, increase the current size
        if self.arr[hashIndex] is None or self.arr[hashIndex].key == -1:
            self.size += 1
        self.arr[hashIndex] = temp

    # Function to delete a key value pair
    def deleteNode(self, key):
        # Apply hash function to find index for given key
        hashIndex = self.hashCode(key)
        # finding the node with given key
        while self.arr[hashIndex] is not None:
            # if node found
            if self.arr[hashIndex].key == key:
                temp = self.arr[hashIndex]
                # Insert dummy node here for further use
                self.arr[hashIndex] = self.dummy
                # Reduce size
                self.size -= 1
                return temp.value
            hashIndex += 1
            hashIndex %= self.capacity
        # If not found return None
        return None

    # Function to search the value for a given key
    def get(self, key):
        # Apply hash function to find index for given key
        hashIndex = self.hashCode(key)
        counter = 0
        # finding the node with given key
        while self.arr[hashIndex] is not None:
            # If counter is greater than capacity to avoid infinite loop
            if counter > self.capacity:
                return None
            # if node found return its value
            if self.arr[hashIndex].key == key:
                return self.arr[hashIndex].value
            hashIndex += 1
            hashIndex %= self.capacity
            counter += 1
        # If not found return None
        return 0

    # Return current size
    def sizeofMap(self):
        return self.size

    # Return true if size is 0
    def isEmpty(self):
        return self.size == 0

    # Function to display the stored key value pairs
    def display(self):
        for i in range(self.capacity):
            if self.arr[i] is not None and self.arr[i].key != -1:
                print("key = ", self.arr[i].key,
                      " value = ", self.arr[i].value)


# Driver method to test map class
if __name__ == "__main__":
    h = HashMap()
    h.insertNode(1, 1)
    h.insertNode(2, 2)
    h.insertNode(2, 3)
    h.display()
    print(h.sizeofMap())
    print(h.deleteNode(2))
    print(h.sizeofMap())
    print(h.isEmpty())
    print(h.get(2))
C# 
using System;

class HashNode {
    public int key;
    public int value;
    public HashNode next;

    public HashNode(int key, int value)
    {
        this.key = key;
        this.value = value;
        next = null;
    }
}

class HashMap {
    private HashNode[] table;
    private int capacity;
    private int size;

    public HashMap(int capacity)
    {
        this.capacity = capacity;
        table = new HashNode[capacity];
        size = 0;
    }

    // hash function to find index for a given key
    private int HashCode(int key) { return key % capacity; }

    // function to add key value pair
    public void InsertNode(int key, int value)
    {
        int hashIndex = HashCode(key);
        HashNode newNode = new HashNode(key, value);

        // if the key already exists, update the value
        if (table[hashIndex] != null) {
            HashNode current = table[hashIndex];

            while (current != null) {
                if (current.key == key) {
                    current.value = value;
                    return;
                }
                current = current.next;
            }
        }

        // if the key is new, add a new node to the table
        newNode.next = table[hashIndex];
        table[hashIndex] = newNode;
        size++;
    }

    // function to delete a key value pair
    public int ? DeleteNode(int key)
    {
        int hashIndex = HashCode(key);

        if (table[hashIndex] != null) {
            HashNode current = table[hashIndex];
            HashNode previous = null;

            while (current != null) {
                if (current.key == key) {
                    if (previous == null) {
                        table[hashIndex] = current.next;
                    }
                    else {
                        previous.next = current.next;
                    }
                    size--;
                    return current.value;
                }
                previous = current;
                current = current.next;
            }
        }

        return null;
    }

    // function to get the value for a given key
    public int ? Get(int key)
    {
        int hashIndex = HashCode(key);

        if (table[hashIndex] != null) {
            HashNode current = table[hashIndex];

            while (current != null) {
                if (current.key == key) {
                    return current.value;
                }
                current = current.next;
            }
        }

        return 0;
    }

    // function to get the number of key value pairs in the
    // hashmap
    public int Size() { return size; }

    // function to check if the hashmap is empty
    public bool IsEmpty() { return size == 0; }

    // function to display the key value pairs in the
    // hashmap
    public void Display()
    {
        for (int i = 0; i < capacity; i++) {
            if (table[i] != null) {
                HashNode current = table[i];

                while (current != null) {
                    Console.WriteLine("key = " + current.key
                                      + " value = "
                                      + current.value);
                    current = current.next;
                }
            }
        }
    }
}

class Program {
    static void Main(string[] args)
    {
        HashMap h = new HashMap(20);

        h.InsertNode(1, 1);
        h.InsertNode(2, 2);
        h.InsertNode(2, 3);

        h.Display();

        Console.WriteLine(h.Size());
        Console.WriteLine(h.DeleteNode(2));
        Console.WriteLine(h.Size());
        Console.WriteLine(h.IsEmpty());
        Console.WriteLine(h.Get(2));
    }
}
Javascript 
// template for generic type
class HashNode {
  constructor(key, value) {
    this.key = key;
    this.value = value;
  }
}

// template for generic type
class HashMap {
  constructor() {
    this.capacity = 20;
    this.size = 0;
    this.arr = new Array(this.capacity);

    // Initialise all elements of array as NULL
    for (let i = 0; i < this.capacity; i++) {
      this.arr[i] = null;
    }

    // dummy node with value and key -1
    this.dummy = new HashNode(-1, -1);
  }

  // This implements hash function to find index for a key
  hashCode(key) {
    return key % this.capacity;
  }

  // Function to add key value pair
  insertNode(key, value) {
    const temp = new HashNode(key, value);

    // Apply hash function to find index for given key
    let hashIndex = this.hashCode(key);

    // find next free space
    while (
      this.arr[hashIndex] !== null &&
      this.arr[hashIndex].key !== key &&
      this.arr[hashIndex].key !== -1
    ) {
      hashIndex++;
      hashIndex %= this.capacity;
    }

    // if new node to be inserted
    // increase the current size
    if (
      this.arr[hashIndex] === null ||
      this.arr[hashIndex].key === -1
    ) {
      this.size++;
    }
    this.arr[hashIndex] = temp;
  }

  // Function to delete a key value pair
  deleteNode(key) {
    // Apply hash function to find index for given key
    let hashIndex = this.hashCode(key);

    // finding the node with given key
    while (this.arr[hashIndex] !== null) {
      // if node found
      if (this.arr[hashIndex].key === key) {
        const temp = this.arr[hashIndex];

        // Insert dummy node here for further use
        this.arr[hashIndex] = this.dummy;

        // Reduce size
        this.size--;
        return temp.value;
      }
      hashIndex++;
      hashIndex %= this.capacity;
    }

    // If not found return null
    return null;
  }

  // Function to search the value for a given key
  get(key) {
    // Apply hash function to find index for given key
    let hashIndex = this.hashCode(key);
    let counter = 0;

    // finding the node with given key
    while (this.arr[hashIndex] !== null) {
      if (counter++ > this.capacity) {
        // to avoid infinite loop
        return 0;
      }

      // if node found return its value
      if (this.arr[hashIndex].key === key) {
        return this.arr[hashIndex].value;
      }
      hashIndex++;
      hashIndex %= this.capacity;
    }

    // If not found return null
    return 0;
  }

  // Return current size
  sizeofMap() {
    return this.size;
  }

  // Return true if size is 0
  isEmpty() {
    return this.size === 0;
  }

  // Function to display the stored key value pairs
  display() {
    for (let i = 0; i < this.capacity; i++) {
      if (this.arr[i] !== null && this.arr[i].key !== -1) {
        console.log(`key = ${this.arr[i].key} value = ${this.arr[i].value}`);
      }
    }
  }
}

// Driver method to test map class
const h = new HashMap();
h.insertNode(1,1);
h.insertNode(2,2);
h.insertNode(2,3);
h.display();
console.log(h.sizeofMap());
console.log(h.deleteNode(2));
console.log(h.sizeofMap());
console.log(h.isEmpty());
console.log(h.get(2));

Output
key = 1  value = 1
key = 2  value = 3
2
3
1
0
0

Complexity analysis for Insertion:

  • Time Complexity:
    • Best Case: O(1)
    • Worst Case: O(N). This happens when all elements have collided and we need to insert the last element by checking free space one by one.
    • Average Case: O(1) for good hash function, O(N) for bad hash function
  • Auxiliary Space: O(1)

Complexity analysis for Deletion:

  • Time Complexity:
    • Best Case: O(1)
    • Worst Case: O(N)
    • Average Case: O(1) for good hash function; O(N) for bad hash function
  • Auxiliary Space: O(1) 

Complexity analysis for Searching:

  • Time Complexity:
    • Best Case: O(1)
    • Worst Case: O(N)
    • Average Case: O(1) for good hash function; O(N) for bad hash function
  • Auxiliary Space: O(1) for search operation




Like Article
Suggest improvement
Previous
Implementing our Own Hash Table with Separate Chaining in Java
Next
Maximum possible difference of two subsets of an array
Share your thoughts in the comments

Similar Reads

Program to implement Hash Table using Open Addressing
Implementing our Own Hash Table with Separate Chaining in Java
Quadratic Probing in Hashing
Open Addressing Collision Handling technique in Hashing
What are Hash Functions and How to choose a good Hash Function?
Hash Functions and list/types of Hash functions
Implementing Rabin Karp Algorithm Using Rolling Hash in Java
Comparison of an Array and Hash table in terms of Storage structure and Access time complexity
Various load balancing techniques used in Hash table to ensure efficient access time
Implementation of Hash Table in Python using Separate Chaining
https://media.geeksforgeeks.org/auth/avatar.png
GeeksforGeeks
Article Tags :
Practice Tags :
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox