How to find the Diagonal of a Matrix?
Last Updated :
31 Jul, 2022
British Mathematician Arthur Cayley was the first person to develop the algebraic aspect of the matrix. After that, Psychiat Heisenberg used matrices as a tool to explain his famous Quantum principle. The study of matrices originated while solving different types of simple and complex linear problems, which is cumbersome to solve without matrices. A rectangular array of mn numbers in the form of m horizontal lines called rows, and n vertical lines called columns is called a matrix of order m x n. This arrays is enclosed by [ ] or ( ) or || || . Each number of the m x n matrix is known as the element of the matrix. A matrix is generally denoted by capital alphabetical characters, and its element is denoted by small alphabetical characters with suffix ij, which indicates to row and column number, i.e. aij, is called elements of matrix A.
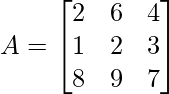
- The elements of the matrix may be scalar or vector quantity.
- A matrix is only an arrangement of numbers; it has no definite value. i.e. [5] ≠ 5.
Some important terms related to matrix
- Elements of a Matrix: Each of the M, N numbers of the Matrix is called an element or an entry of the Matrix.
- Notation of a Matrix: A matrix is generally represented by the symbols [aij] or (aij) or ||aij||. A matrix is denoted by a single capital letter such as A, B, C etc.
- Order of a Matrix: A matrix having m rows and n columns is said to be a matrix of order m x n.
Diagonal Elements of a Matrix
An element aij of a matrix A = [aij] is a diagonal elements of matrix if i = j, such as when rows and column suffixes are equal. Thus, a11 , a22 , a33, a44, … so on are diagonal elements of the matrix A = [aij].
- Principal Diagonal of a Matrix
The principal diagonal is also known as the leading diagonal. The diagonal of a square matrix running from the upper left entities to the lower right entities are principal diagonal of a matrix.
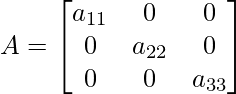
Here, Principal Diagonal elements are non-zeroes.
It’s also called anti diagonal of a matrix. The diagonal of a square matrix running from the upper right entities to the lower-left entities is called the counter diagonal of a matrix.
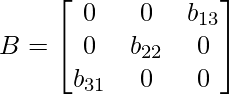
Here, Counter diagonal elements are non-zeroes.
Note: Above, we considered examples in principal and counter diagonal. Elements of the matrix other than diagonal are considered as zeroes for better clarification.
Sample problems
Question 1: Find out the diagonal element of the below matrix.
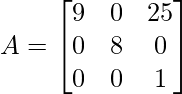
Solution:
As we know, To find the diagonal of matrix or diagonal elements is not a heavy task; it is just a basic practice of matrices. If anyone told us to find the diagonal element, we only found the principal diagonal as a result. which is running from the upper left entities to the lower right entities
Diagonal element of matrix,
a11 = 9, a22 = 8, a33 = 1
Question 2: Find trace of matrix A, given below.
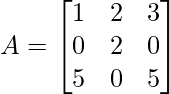
Solution:
Trace of matrix: It’s actually sum of principal diagonal element.
tr(A) = a11 + a22 + a33;
So, after observation of matrix
We can say, a11 = 1, a22 = 2, a33 = 5
tr(a) = 1 + 2 + 5 = 8
Question 3: Find the inverse of diagonal matrix:
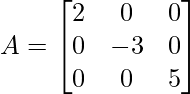
Solution:
Determinant of matrix of A,
|A| = -30
Adjoint of matrix A,
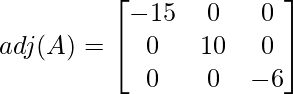
We know inverse of matrix A is: A-1 = \frac{adj(A)}{|A|}
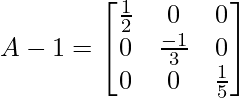
Question 4: Find value of a11 + a23 – a22 + a31 from given below matrix.
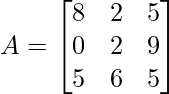
Solution:
We know standard matrix syntax.
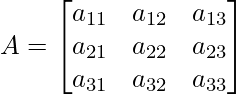
By comparing it to our matrix we can say,
a11 = 8, a23 = 9, a22 = 2, a31 = 5
Required result: a11 + a23 – a22 + a31 = 8 + 9 – 2 – 5 = 10
Question 5: Find the product of diagonal element of below matrix:
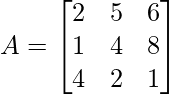
Solution:
The diagonal element of the above matrix are 2, 4, and 1, respectively
Product of diagonal: 2 × 4 × 1 = 8
Question 6: Find the determinant of the matrix given below:
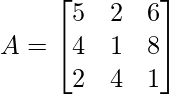
Solution:
Determinant of matrix A,
|A| = 5 (1 – 32) – 2 (16 – 4) + 6 (16 – 2)
|A| = 5(-31) – 2(12) + 6(14)
|A| = -155 – 24 + 84 = -95
Question 7: Find the sum of counter diagonal of matrix , common element of principle and counter diagonal:
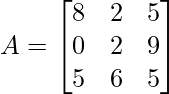
Solution:
We know square matrix running from the upper right entities to the lower left entities are counter diagonals of matrix.
So, counter diagonal elements are
a13 = 5 a22 = 2 a31 = 5
The common element of principal and counter diagonal is 2.
Share your thoughts in the comments
Please Login to comment...