How to Find Standard Deviation in R?
Last Updated :
05 Jul, 2023
In this article, we will discuss how to find the Standard Deviation in R Programming Language. Standard deviation R is the measure of the dispersion of the values. It can also be defined as the square root of variance.
Formula of sample standard deviation:
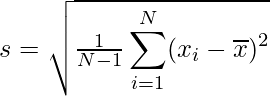
where,
- s = sample standard deviation
- N = Number of entities
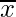 = Mean of entities
= Mean of entities
Basically, there are two different ways to calculate standard Deviation in R Programming language, both of them are discussed below.
Method 1: Naive approach
In this method of calculating the standard deviation, we will be using the above standard formula of the sample standard deviation in R language.
Example 1:
R
v <- c(12,24,74,32,14,29,84,56,67,41)
s<-sqrt(sum((v-mean(v))^2/(length(v)-1)))
print(s)
|
Output:
[1] 25.53886
Example 2:
R
v <- c(1.8,3.7,9.2,4.7,6.1,2.8,6.1,2.2,1.4,7.9)
s<-sqrt(sum((v-mean(v))^2/(length(v)-1)))
print(s)
|
Output:
[1] 2.676004
Method 2: Using sd()
The sd() function is used to return the standard deviation.
Syntax: sd(x, na.rm = FALSE)
Parameters:
- x: a numeric vector, matrix or data frame.
- na.rm: missing values be removed?
Return: The sample standard deviation of x.
Example 1:
R
v <- c(12,24,74,32,14,29,84,56,67,41)
s<-sd(v)
print(s)
|
Output:
[1] 25.53886
Example 2:
R
v <- c(71,48,98,65,45,27,39,61,50,24,17)
s1<-sqrt(sum((v-mean(v))^2/(length(v)-1)))
print(s1)
s2<-sd(v)
print(s2)
|
Output:
[1] 23.52175
Example 3:
R
v <- c(1.8,3.7,9.2,4.7,6.1,2.8,6.1,2.2,1.4,7.9)
s1<-sqrt(sum((v-mean(v))^2/(length(v)-1)))
print(s1)
s2<-sd(v)
print(s2)
|
Output:
[1] 2.676004
Calculate the Standard Deviation of the Data Frame:
We can calculate the standard deviation of the data frame using both methods. we can take the iris dataset and for every column, we will calculate the standard deviation.
Example 1:
R
data(iris)
sd(iris$Sepal.Length)
sd(iris$Sepal.Width)
sd(iris$Petal.Length)
sd(iris$Petal.Width)
|
Output:
[1] 0.8280661
[1] 0.4358663
[1] 1.765298
[1] 0.7622377
We can also calculate the Standard deviation for the entire data frame together with the help of apply function.
R
data(iris)
std_deviation <- apply(iris[, 1:4], 2, sd)
print(std_deviation)
|
Output:
Sepal.Length Sepal.Width Petal.Length Petal.Width
0.8280661 0.4358663 1.7652982 0.7622377
Columns 1 through 4 of the iris dataset, which are the numerical columns carrying the variable measurements, are chosen using the expression iris[, 1:4] in the code above.
The sd function is applied to each column (marked by 2) of the chosen subset of the iris dataset using the apply function. The resulting standard deviation values are saved in the std_deviation vector for each column.
Share your thoughts in the comments
Please Login to comment...