How to calculate the mean using Step deviation method?
Last Updated :
13 Oct, 2021
In simple words, statistics implies the process of gathering, sorting, examine, interpret and then present the data in an understandable manner so as to enable one to form an opinion of it and take necessary action, if necessary. Examples:
- A teacher collecting students’ marks, organizing them in ascending or descending manner, and calculating the average class marks, or finding the number of students who failed, informing them so that they start working hard.
- Government officials collecting data for the census, and comparing it with previous records to see whether population growth is in control or not.
- Analyzing the number of followers of a particular religion of a country.
Statistical Tools
The most popular tools of statistics are as follows:
- Arithmetic Mean: Also known as average, the arithmetic mean for a given set of data is calculated by adding up the numbers in the data and dividing the sum so obtained with the number of observations.
- Median: Such a value as separates the higher and lower values of a given set of statistical data is called the median.
- Mode: Such a value as occurs most frequently in a given series of statistical data is called the mode.
- Standard Deviation: Such a value as indicates the extent to which certain values of a statistical series tend to vary or disperse from its mean or median is called standard deviation.
- Range: Such a value depicts the difference between the highest and lowest values in a series.
- Correlation: Such a statistical tool as helps study the relationship between two variables is called correlation.
Arithmetic Mean
Arithmetic mean also known as average, arithmetic mean for a given set of data is calculated by adding up the numbers in the data and dividing the sum so obtained with the number of observations. It is the most popular method of central tendency.
Properties of Arithmetic Mean
- Deviations from the arithmetic mean of all items in a statistical series would always add up to zero, i.e. ∑(x – X) = 0.
- The squared deviations from the arithmetic mean is always minimum, i.e., less than the sum of such square deviations from other values like the median, mode, or another tool.
- Replacing all the items in a statistical series with its arithmetic mean has no effect on the sum of the said items.
Using Direct Method
The arithmetic mean is calculated using the following formula,
Sum of observation/Number of observations
Mean of the series = x̄ = Σx/ N.
The formula discussed above pertains to the direct method of calculating the arithmetic mean. But in the case where the calculation becomes tedious owing to larger observations in a data set, other methods can be used to calculate the arithmetic mean, one of such methods being the step-deviation method.
Step Deviation Method
Whenever the data values are large, and calculation is tedious, the step deviation method is applied. The following steps are used while applying the step deviation method to calculate the arithmetic mean:
- Choose one observation from the data set and mark it as the assumed mean of the whole series. In the case of grouped data, it is not possible to pick an observation from the class intervals, so one first needs to calculate the class marks of mid-points of the intervals and mark one as the assumed mean.
- The next step is to find deviations from the assumed mean (A) by deducting the mean so assumed from all the other observations. d = X – A.
- Next, we are supposed to calculate the step deviations from the deviations obtained above, by finding a common factor, denoted by c, of all the values (deviations), dividing all by this factor, and labelling the step deviations as d1.
- Multiply the step deviations with the frequencies and take up the sum of the numbers so obtained.
- Apply the formula:
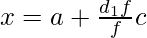 , where Σd1 is the sum of all the step deviations multiplied by respective frequencies and c represents the common factor.
, where Σd1 is the sum of all the step deviations multiplied by respective frequencies and c represents the common factor. - The number so obtained is the arithmetic mean of the given data set.
Thus the formula for the calculation of arithmetic mean by step deviation method is 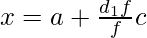
Example: Calculate the arithmetic mean for the following data set using the step deviation method:
Marks
| Number of Students |
0 – 10
| 5
|
10 – 20
| 12
|
20 – 30
| 14
|
30 – 40
| 10
|
40 – 50
| 5
|
Solution:
Marks
| f
| m
| d = m – A
A = 25
| d1 = d/ c
c = 10
| fd1
|
0 – 10
| 5
| 5
| 5 – 25 = −20
| −2
| −10
|
10 – 20
| 12
| 15
| 15 – 25 = −10
| −1
| −12
|
20 – 30
| 14
| A = 25
| 25 – 25 = 0
| 0
| 0
|
30 – 40
| 10
| 35
| 35 – 25 = 10
| 1
| 10
|
40 – 50
| 8
| 45
| 45 – 25 = 20
| 2
| 16
|
| | Σf = 49
| |
| | Σfd1 = 4
|
Mean = X̄ = 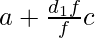
= 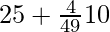
= 25 + 0.81
= 25.81
Hence, Arithmetic Mean of the given data set is 25.81
Sample Questions
Question 1. Calculate the mean using the step deviation method:
Marks
| Number of students
|
10 – 20
| 5
|
20 – 30
| 3
|
30 – 40
| 4
|
40 – 50
| 7
|
50 – 60
| 2
|
60 – 70
| 6
|
70 – 80
| 13
|
Solution:
| Marks | f
| m
| d = m – A
A = 45
| d1 = d/ c
c = 10
| fd1
|
| 10 – 20 | 5
| 15 | −30
| −3
| −15
|
| 20 – 30 | 3
| 25 | −20
| −2
| −6
|
| 30 – 40 | 4
| 35 | −10
| −1
| −4
|
| 40 – 50 | 7
| 45 | 0
| 0
| 0
|
| 50 – 60 | 2
| 55 | 10
| 1
| 2
|
| 60 – 70 | 6
| 65 | 20
| 2
| 12
|
| 70 – 80 | 13
| 75 | 30
| 3
| 39
|
| | Σf = 40
| | | | Σfd1 = 28 |
Mean = X̄ = 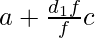
= 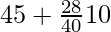
= 45 + 7
= 52
Hence, Arithmetic Mean of the given data set is 52.
Question 2. Calculate the mean using the step deviation method:
Class Intervals
| Frequency
|
−40 to −30
| 10
|
−30 to −20
| 28
|
−20 to −10
| 30
|
−10 to 0
| 42
|
0 to 10
| 65
|
10 to 20
| 180
|
20 to 30
| 10
|
Solution:
Class Intervals
| f
| m
| d = m – A
A = −5
| d1 = d/c
c = 10
| fd1
|
−40 to −30
| 10
| −35
| −30
| −3
| −30
|
−30 to −20
| 28
| −25
| −20
| −2
| −56
|
−20 to −10
| 30
| −15
| −10
| −1
| −30
|
−10 to 0
| 42
| −5
| 0
| 0
| 0
|
0 to 10
| 65
| 5
| 10
| 1
| 65
|
10 to 20
| 180
| 15
| 20
| 2
| 180
|
20 to 30
| 10
| 25
| 30
| 3
| 30
|
| | Σf = 365 | | | | Σfd1 = 159 |
Mean = X̄ = 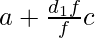
= 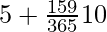
= −0.64
Hence arithmetic mean is −0.64
Question 3. Calculate the mean using the step deviation method:
| Wages | Number of workers |
| 0 – 10 | 22
|
| 10 – 20 | 38
|
| 20 – 30 | 46
|
| 30 – 40 | 35
|
| 40 – 50 | 19
|
Solution:
Wages
| f
| m
| d = m – A
A = 25
| d1 = d/c
c = 10
| fd1
|
0 – 10
| 22
| 5
| −20
| −2
| −44
|
10 – 20
| 38
| 15
| −10
| −1
| −38
|
20 – 30
| 46
| 25
| 0
| 0
| 0
|
30 – 40
| 35
| 35
| 10
| 1
| 35
|
40 – 50
| 19
| 45
| 20
| 2
| 38
|
| Σf = 160
|
|
|
| Σfd1 = −9
|
Mean = X̄ = 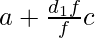
= 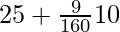
= 24.44
Hence the arithmetic mean is 24.44
Question 4. Calculate the mean using the step deviation method:
Age
| Number of People
|
0 – 20
| 4
|
20 – 40
| 10
|
40 – 60
| 15
|
60 – 80
| 20
|
80 – 100
| 11
|
Solution:
Age
| f
| m
| d = m – A
A = 50
| d1 = d/c
c = 20
| fd1
|
0 – 20
| 4
| 10
| −40
| −2
| −8
|
20 – 40
| 10
| 30
| −20
| −1
| −10
|
40 – 60
| 15
| 50
| 0
| 0
| 0
|
60 – 80
| 20
| 70
| 20
| 1
| 20
|
80 – 100
| 11
| 90
| 40
| 2
| 22
|
| | Σf = 60 | | | | Σfd1 = 24 |
Mean = X̄ = 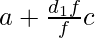
= 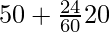
= 50 + 8
= 58
Hence arithmetic mean is 58.
Share your thoughts in the comments
Please Login to comment...