Generalized Linear Models
Last Updated :
02 May, 2023
Prerequisite:
Generalized Linear Models (GLMs) are a class of regression models that can be used to model a wide range of relationships between a response variable and one or more predictor variables. Unlike traditional linear regression models, which assume a linear relationship between the response and predictor variables, GLMs allow for more flexible, non-linear relationships by using a different underlying statistical distribution.
Some of the features of GLMs include:
- Flexibility: GLMs can model a wide range of relationships between the response and predictor variables, including linear, logistic, Poisson, and exponential relationships.
- Model interpretability: GLMs provide a clear interpretation of the relationship between the response and predictor variables, as well as the effect of each predictor on the response.
- Robustness: GLMs can be robust to outliers and other anomalies in the data, as they allow for non-normal distributions of the response variable.
- Scalability: GLMs can be used for large datasets and complex models, as they have efficient algorithms for model fitting and prediction.
- Ease of use: GLMs are relatively easy to understand and use, especially compared to more complex models such as neural networks or decision trees.
- Hypothesis testing: GLMs allow for hypothesis testing and statistical inference, which can be useful in many applications where it’s important to understand the significance of relationships between variables.
- Regularization: GLMs can be regularized to reduce overfitting and improve model performance, using techniques such as Lasso, Ridge, or Elastic Net regression.
- Model comparison: GLMs can be compared using information criteria such as AIC or BIC, which can help to choose the best model among a set of alternatives.
Some of the disadvantages of GLMs include:
- Assumptions: GLMs make certain assumptions about the distribution of the response variable, and these assumptions may not always hold.
- Model specification: Specifying the correct underlying statistical distribution for a GLM can be challenging, and incorrect specification can result in biased or incorrect predictions.
- Overfitting: Like other regression models, GLMs can be prone to overfitting if the model is too complex or has too many predictor variables.
- Overall, GLMs are a powerful and flexible tool for modeling relationships between response and predictor variables, and are widely used in many fields, including finance, marketing, and epidemiology. If you’re interested in learning more about GLMs, you might consider reading an introductory textbook on regression analysis, such as “An Introduction to Generalized Linear Models” by Annette J. Dobson and Annette J. Barnett.
- Limited flexibility: While GLMs are more flexible than traditional linear regression models, they may still not be able to capture more complex relationships between variables, such as interactions or non-linear effects.
- Data requirements: GLMs require a sufficient amount of data to estimate model parameters and make accurate predictions, and may not perform well with small or imbalanced datasets.
- Model assumptions: GLMs rely on certain assumptions about the distribution of the response variable and the relationship between the response and predictor variables, and violation of these assumptions can lead to biased or incorrect predictions.
The following article discusses the Generalized linear models (GLMs) which explains how Linear regression and Logistic regression are a member of a much broader class of models. GLMs can be used to construct the models for regression and classification problems by using the type of distribution which best describes the data or labels given for training the model. Below given are some types of datasets and the corresponding distributions which would help us in constructing the model for a particular type of data (The term data specified here refers to the output data or the labels of the dataset).
- Binary classification data – Bernoulli distribution
- Real valued data – Gaussian distribution
- Count-data – Poisson distribution
To understand GLMs we will begin by defining exponential families. Exponential families are a class of distributions whose probability density function(PDF) can be molded into the following form:
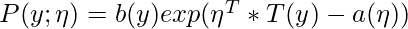

Proof – Bernoulli distribution is a member of the exponential family.
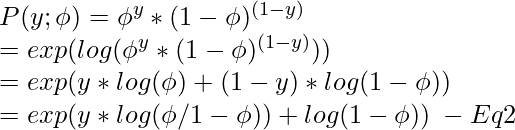
Therefore, on comparing
Eq1 and Eq2 :
\eta = log(\phi/1-\phi)\\
\phi = 1/1+e^{-\eta} - Eq 3\\
b(y) = 1\\ T(y) = y\\ a(\eta) = -log(1-\phi)
Note: As mentioned above the value of phi (which is the same as the activation or sigmoid function for Logistic regression) is not a coincidence. And it will be proved later in the article how Logistic regression model can be derived from the Bernoulli distribution.
Proof – Gaussian distribution is a member of the exponential family.
P(y, mu) = 1/\sqrt{2\pi} * exp(-1/2*(y-\mu)^2)\\ \hspace{1.5cm} = 1/\sqrt{2\pi}*exp(-1/2*y^{2}) * exp(\mu*y-1/2*\mu^{2}) - Eq3\\
Therefore, on comparing Eq1 and Eq3:
b(y) = 1/\sqrt{2\pi}*exp(-1/2*y^{2})\\ \eta = \mu\\ T(y) = y\\ a(\eta) = 1/2*\eta^2\\
Constructing GLMs: To construct GLMs for a particular type of data or more generally for linear or logistic classification problems the following three assumptions or design choices are to be considered:
![Rendered by QuickLaTeX.com y|x;\theta \sim exponential\hspace{1mm} family(\eta)\\ Given \hspace{1mm}x\hspace{1mm} our\hspace{1mm} goal\hspace{1mm} is\hspace{1mm} to\hspace{1mm} predict \hspace{1mm}T(y)\hspace{1mm} which \hspace{1mm}is \hspace{1mm}equal \hspace{1mm}to\hspace{1mm} y \hspace{1mm}in\hspace{1mm} our\hspace{1mm} case \hspace{1mm}or \hspace{1mm}h(x) = E[y|x] = \mu\\ \eta = \theta^T * x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8028c08100c8c1711abb5b262d3f9aec_l3.png)
The first assumption is that if x is the input data parameterized by theta the resulting output or y will be a member of the exponential family. This means if we are provided with some labeled data our goal is to find the right parameters theta which fits the given model as closely as possible. The third assumption is the least justified and can be considered as a design choice.
Linear Regression Model: To show that Linear Regression is a special case of the GLMs. It is considered that the output labels are continuous values and are therefore a Gaussian distribution. So, we have
![Rendered by QuickLaTeX.com y|x;\theta \sim \mathcal{N}(\mu, \sigma^2) \\ h_\theta(x) = E[y|x;\theta]\\ \hspace{0.9cm} = \mu\\ \hspace{0.9cm} = \eta\\ \hspace{0.9cm} = \theta^Tx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-57002eb51beb014d68e143794f1c2709_l3.png)
The first equation above corresponds to the first assumption that the output labels (or target variables) should be the member of an exponential family, the Second equation corresponds to the assumption that the hypothesis is equal the expected value or mean of the distribution and lastly, the third equation corresponds to the assumption that natural parameter and the input parameters follow a linear relationship.
Logistic Regression Model: To show that Logistic Regression is a special case of the GLMs. It is considered that the output labels are Binary valued and are therefore a
Bernoulli distribution. So, we have
![Rendered by QuickLaTeX.com y|x;\theta \sim Bernoulli(\phi) \\ h_\theta(x) = E[y|x;\theta]\\ \hspace{0.9cm} = \mu\\ \hspace{0.9cm} = 1/1+e^{-\eta}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3b5d7c2e847b41422d62cd4c7d11a4ab_l3.png)
From the third assumption, it is proven that:
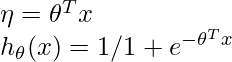
The function that maps the natural parameter to the canonical parameter is known as the canonical response function (here, the log-partition function) and the inverse of it is known as the canonical link function.
Therefore by using the three assumptions mentioned before it can be proved that the Logistic and Linear Regression belongs to a much larger family of models known as GLMs.
Share your thoughts in the comments
Please Login to comment...