Friends Pairing Problem
Last Updated :
12 Dec, 2022
Given n friends, each one can remain single or can be paired up with some other friend. Each friend can be paired only once. Find out the total number of ways in which friends can remain single or can be paired up.
Examples:
Input : n = 3
Output : 4
Explanation:
{1}, {2}, {3} : all single
{1}, {2, 3} : 2 and 3 paired but 1 is single.
{1, 2}, {3} : 1 and 2 are paired but 3 is single.
{1, 3}, {2} : 1 and 3 are paired but 2 is single.
Note that {1, 2} and {2, 1} are considered same.
Mathematical Explanation:
The problem is simplified version of how many ways we can divide n elements into multiple groups.
(here group size will be max of 2 elements).
In case of n = 3, we have only 2 ways to make a group:
1) all elements are individual(1,1,1)
2) a pair and individual (2,1)
In case of n = 4, we have 3 ways to form a group:
1) all elements are individual (1,1,1,1)
2) 2 individuals and one pair (2,1,1)
3) 2 separate pairs (2,2)
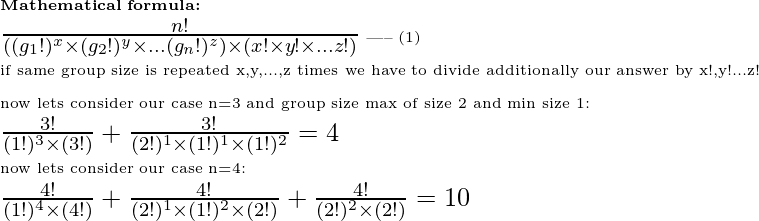
For n-th person there are two choices:1) n-th person remains single, we recur for f(n – 1)2) n-th person pairs up with any of the remaining n – 1 persons. We get (n – 1) * f(n – 2)Therefore we can recursively write f(n) as:f(n) = f(n – 1) + (n – 1) * f(n – 2)
Since the above recursive formula has overlapping subproblems, we can solve it using Dynamic Programming.
C++
#include <bits/stdc++.h>
using namespace std;
int countFriendsPairings(int n)
{
int dp[n + 1];
for (int i = 0; i <= n; i++) {
if (i <= 2)
dp[i] = i;
else
dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
}
return dp[n];
}
int main()
{
int n = 4;
cout << countFriendsPairings(n) << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
static int countFriendsPairings(int n)
{
int dp[] = new int[n + 1];
for (int i = 0; i <= n; i++) {
if (i <= 2)
dp[i] = i;
else
dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
}
return dp[n];
}
public static void main(String[] args)
{
int n = 4;
System.out.println(countFriendsPairings(n));
}
}
|
Python3
def countFriendsPairings(n):
dp = [0 for i in range(n + 1)]
for i in range(n + 1):
if(i <= 2):
dp[i] = i
else:
dp[i] = dp[i - 1] + (i - 1) * dp[i - 2]
return dp[n]
n = 4
print(countFriendsPairings(n))
|
C#
using System;
class GFG {
static int countFriendsPairings(int n)
{
int[] dp = new int[n + 1];
for (int i = 0; i <= n; i++) {
if (i <= 2)
dp[i] = i;
else
dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
}
return dp[n];
}
public static void Main()
{
int n = 4;
Console.Write(countFriendsPairings(n));
}
}
|
PHP
<?php
function countFriendsPairings($n)
{
$dp[$n + 1] = 0;
for ($i = 0; $i <= $n; $i++)
{
if ($i <= 2)
$dp[$i] = $i;
else
$dp[$i] = $dp[$i - 1] +
($i - 1) *
$dp[$i - 2];
}
return $dp[$n];
}
$n = 4;
echo countFriendsPairings($n) ;
?>
|
Javascript
<script>
function countFriendsPairings(n)
{
let dp = [];
for (let i = 0; i <= n; i++) {
if (i <= 2)
dp[i] = i;
else
dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
}
return dp[n];
}
let n = 4;
document.write(countFriendsPairings(n));
</script>
|
Time Complexity : O(n)
Auxiliary Space : O(n)
Another approach: (Using recursion)
C++
#include <bits/stdc++.h>
using namespace std;
int dp[1000];
int countFriendsPairings(int n)
{
if (dp[n] != -1)
return dp[n];
if (n > 2)
return dp[n] = countFriendsPairings(n - 1) + (n - 1) * countFriendsPairings(n - 2);
else
return dp[n] = n;
}
int main()
{
memset(dp, -1, sizeof(dp));
int n = 4;
cout << countFriendsPairings(n) << endl;
}
|
Java
import java.io.*;
class GFG {
static int[] dp = new int[1000];
static int countFriendsPairings(int n)
{
if (dp[n] != -1)
return dp[n];
if (n > 2)
return dp[n] = countFriendsPairings(n - 1) + (n - 1) * countFriendsPairings(n - 2);
else
return dp[n] = n;
}
public static void main(String[] args)
{
for (int i = 0; i < 1000; i++)
dp[i] = -1;
int n = 4;
System.out.println(countFriendsPairings(n));
}
}
|
Python3
dp = [-1] * 1000
def countFriendsPairings(n):
global dp
if(dp[n] != -1):
return dp[n]
if(n > 2):
dp[n] = (countFriendsPairings(n - 1) +
(n - 1) * countFriendsPairings(n - 2))
return dp[n]
else:
dp[n] = n
return dp[n]
n = 4
print(countFriendsPairings(n))
|
C#
using System;
class GFG {
static int[] dp = new int[1000];
static int countFriendsPairings(int n)
{
if (dp[n] != -1)
return dp[n];
if (n > 2)
return dp[n] = countFriendsPairings(n - 1) + (n - 1) * countFriendsPairings(n - 2);
else
return dp[n] = n;
}
static void Main()
{
for (int i = 0; i < 1000; i++)
dp[i] = -1;
int n = 4;
Console.Write(countFriendsPairings(n));
}
}
|
PHP
<?php
function countFriendsPairings($n)
{
$dp = array_fill(0, 1000, -1);
if($dp[$n] != -1)
return $dp[$n];
if($n > 2)
{
$dp[$n] = countFriendsPairings($n - 1) + ($n - 1) *
countFriendsPairings($n - 2);
return $dp[$n];
}
else
{
$dp[$n] = $n;
return $dp[$n];
}
}
$n = 4;
echo countFriendsPairings($n)
?>
|
Javascript
<script>
let dp = new Array(1000);
function countFriendsPairings(n)
{
if (dp[n] != -1)
return dp[n];
if (n > 2)
return dp[n] = countFriendsPairings(n - 1)
+ (n - 1) * countFriendsPairings(n - 2);
else
return dp[n] = n;
}
for (let i = 0; i < 1000; i++)
dp[i] = -1;
let n = 4;
document.write(countFriendsPairings(n));
</script>
|
Time Complexity : O(n)
Auxiliary Space : O(n)
Since the above formula is similar to fibonacci number, we can optimize the space with an iterative solution.
C++
#include <bits/stdc++.h>
using namespace std;
int countFriendsPairings(int n)
{
int a = 1, b = 2, c = 0;
if (n <= 2) {
return n;
}
for (int i = 3; i <= n; i++) {
c = b + (i - 1) * a;
a = b;
b = c;
}
return c;
}
int main()
{
int n = 4;
cout << countFriendsPairings(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int countFriendsPairings(int n)
{
int a = 1, b = 2, c = 0;
if (n <= 2) {
return n;
}
for (int i = 3; i <= n; i++) {
c = b + (i - 1) * a;
a = b;
b = c;
}
return c;
}
public static void main(String[] args)
{
int n = 4;
System.out.println(countFriendsPairings(n));
}
}
|
Python3
def countFriendsPairings(n):
a, b, c = 1, 2, 0;
if (n <= 2):
return n;
for i in range(3, n + 1):
c = b + (i - 1) * a;
a = b;
b = c;
return c;
n = 4;
print(countFriendsPairings(n));
|
C#
using System;
class GFG {
static int countFriendsPairings(int n)
{
int a = 1, b = 2, c = 0;
if (n <= 2) {
return n;
}
for (int i = 3; i <= n; i++) {
c = b + (i - 1) * a;
a = b;
b = c;
}
return c;
}
public static void Main(String[] args)
{
int n = 4;
Console.WriteLine(countFriendsPairings(n));
}
}
|
PHP
<?php
function countFriendsPairings($n)
{
$a = 1;
$b = 2;
$c = 0;
if ($n <= 2)
{
return $n;
}
for ($i = 3; $i <= $n; $i++)
{
$c = $b + ($i - 1) * $a;
$a = $b;
$b = $c;
}
return $c;
}
$n = 4;
print(countFriendsPairings($n));
?>
|
Javascript
<script>
function countFriendsPairings(n)
{
let a = 1, b = 2, c = 0;
if (n <= 2) {
return n;
}
for (let i = 3; i <= n; i++) {
c = b + (i - 1) * a;
a = b;
b = c;
}
return c;
}
let n = 4;
document.write(countFriendsPairings(n));
</script>
|
Time Complexity : O(n)
Auxiliary Space : O(1)
Another Approach: Since we can solve the above problem using maths, the solution below is done without using dynamic programming.
C++
#include <bits/stdc++.h>
using namespace std;
void preComputeFact(vector<long long int>& fact, int n)
{
for(int i = 1; i <= n; i++)
fact.push_back(fact[i - 1] * i);
}
int countFriendsPairings(vector<long long int> fact,
int n)
{
int ones = n, twos = 1, ans = 0;
while (ones >= 0)
{
ans += fact[n] / (twos * fact[ones] *
fact[(n - ones) / 2]);
ones -= 2;
twos *= 2;
}
return ans;
}
int main()
{
vector<long long int> fact;
fact.push_back(1);
preComputeFact(fact, 100);
int n = 4;
cout << countFriendsPairings(fact, n) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG{
static Vector<Integer> fact;
static void preComputeFact( int n)
{
for(int i = 1; i <= n; i++)
fact.add(fact.elementAt(i - 1) * i);
}
static int countFriendsPairings(int n)
{
int ones = n, twos = 1, ans = 0;
while (ones >= 0)
{
ans += fact.elementAt(n) / (twos * fact.elementAt(ones) *
fact.elementAt((n - ones) / 2));
ones -= 2;
twos *= 2;
}
return ans;
}
public static void main(String[] args)
{
fact = new Vector<>();
fact.add(1);
preComputeFact(100);
int n = 4;
System.out.print(countFriendsPairings(n) +"\n");
}
}
|
Python3
fact = [1]
def preComputeFact(n):
for i in range(1, n+1):
fact.append((fact[i-1]*i))
def countFriendsPairings(n):
ones = n
twos = 1
ans = 0
while(ones >= 0):
ans = ans + (fact[n]//(twos*fact[ones]*fact[(n-ones)//2]))
ones = ones - 2
twos = twos * 2
return(ans)
preComputeFact(1000)
n = 4
print(countFriendsPairings(n))
|
C#
using System;
using System.Collections.Generic;
public class GFG
{
static List<int> fact = new List<int>();
static void preComputeFact(int n)
{
for (int i = 1; i <= n; i++) {
fact.Add(fact[i - 1] * i);
}
}
static int countFriendsPairings(int n)
{
int ones = n;
int twos = 1;
int ans = 0;
while (ones >= 0) {
ans += fact[n]
/ (twos * fact[ones]
* fact[(n - ones) / 2]);
ones -= 2;
twos *= 2;
}
return ans;
}
static public void Main()
{
fact.Add(1);
preComputeFact(100);
int n = 4;
Console.Write(countFriendsPairings(n));
}
}
|
Javascript
<script>
let fact = [1];
function preComputeFact(n)
{
for(let i=1;i<n+1;i++)
{
fact.push((fact[i-1]*i));
}
}
function countFriendsPairings(n)
{
let ones = n
let twos = 1;
let ans = 0;
while(ones >= 0)
{
ans = ans + Math.floor(fact[n]/(twos*fact[ones]*
fact[(n-ones)/2]))
ones = ones - 2
twos = twos * 2
}
return ans;
}
preComputeFact(1000)
n = 4
document.write(countFriendsPairings(n))
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(n)
Share your thoughts in the comments
Please Login to comment...