Flow of Electric Charges in a Metallic Conductor
Last Updated :
12 Oct, 2022
Electricity is the flow of electric charges through a metal. All charges present in a conductor whether free or bound, are considered to be at rest. Electric Charge is the property of a matter due to which it experiences and produces electrical and magnetic effects. Charges in motion produce an electric current. Such current occurs in many situations under certain circumstances. If an electric field is applied to an electric charge, it will experience a force. It will move if it is free to do so, generating a current. There exist two types of charges in nature, positive charge and negative charge. Charges with the same electrical sign repel each other and those with the opposite electrical sign attract each other. The S.I. unit of charge is coulombs (C).
Electric Current
Assume a small area in which both the positive and negative charges can flow in forwarding and backward directions across the area. Let q+ be the net amount of positive charges that flow in the forwarding direction across the area and q– be the net amount of negative charges that flows in a forward direction across the area. Let t be the time interval. The total amount of charge flowing through the area in the forward direction in the given time interval t is, q=q+-q–. For a steady current, q is proportional to t.
I = q/t
where,
- I is the current
- q is the charge value
- t is the time taken
It denotes the current across the area in the forwarding direction and if the value is negative, it implies the flow of current in the backward direction. When the current is not steady we define it as follows. During the time interval Δt [i.e. between times t and (t+Δt)] the net amount of charge flowing across the conductor be ΔQ. Then the current across the conductor at time t is given by the value of the ratio of ΔQ to Δt in the limit of Δt tending to zero.
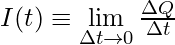
The SI unit of electric current is Ampere and it is denoted by the letter A. Ampere is defined as one coulomb of charge moving past a point in one second.
Flow of Electric Charges in Metallic Conductors
Current is produced in a conductor due to the free movement of electric charges in it. The electric charge experience a force if an electric field is applied to it. The atmosphere too contains charged particles in the upper layer (ionosphere). In an atom both the positively charged nuclei and negatively charged electrons are bound together thus they are not free to move. Solid metals are generally considered good conductors, in these materials most electrons are free to move. An electric charge is developed in them when an electric field is applied. In metallic conductors, the atoms are tightly bound to each other due to which the current is carried by the negatively charged electrons in the background of fixed positive ions.
Metals have a large number of free electrons (approximately 1023 free electrons per meter cube). It is also termed as electron density of the metal. This value varies for different metals. In the absence of an electric field, the electrons in a conductor move randomly due to their thermal energies. As all the electrons are moving in random directions the net thermal velocity is zero. Thus, there are no net motions of electrons in a particular direction in the absence of an electric field. As there is no particular movement of electrons the current generated is zero.

Movement of electrons in a conductor
Imagine an electric field (E) is applied to a metallic conductor in the shape of a cylinder of radius R. Consider two thin discs with the same radius as the cylinder and put positive charge +Q scattered over one disc and similarly put negative charge -Q at the other side. Attach the discs to the two flat surfaces of the cylinder. An electric field is created and is directed from the positive towards the negative charge. The electrons will be accelerated towards +Q (i.e. opposite to the direction of the applied electric field) due to this field and will move to neutralize these charges. This movement of electrons due to this field will generate an electric current. Hence there will be current in the conductor for a concise while and no current after that.

Flow of electrons in a conductor
Solved Examples on Charge Flow
Problem 1: The density of free electrons in a copper conductor is estimated to be 8.5 x 1028 m-3. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of the cross-section of the wire is 2.0 x 10-6m2 and it carries a current of 3.0 A.
Solution:
Density of free electron in a copper conductor, n = 8.5 x 1028 m-3
Length of the copper wire, l = 3.0 m
Area of cross-section of the wire, A = 2.0 x 10-6 m2
Current carried by the wire, I = 3.0 A, which is given by,
I=nAeVd
Where,
e = Electric charge = 1.6 x 10-19 C
Vd = Drift velocity = Length of the wire(l) / Time taken to cover l(t)
I = nAe(l/t)
t = nAel/I
t = 3 x 8.5 x 1028 x 2 x 10-6 x 1.6 x 10-19 / 3.0
t = 2.7 x 104 s
Hence, the time taken by an electron to drift from one end of the wire to the other is 2.7 x 104 s.
Problem 2: Force F is acting between two-point charges. If a sheet of metal (εr= 8) is placed between these charges, then what will be the force?
Solution:
We know,
F = ( 1/(4 π ϵ0K)) ( |q1| |q2| / r2)
= F/K
= F/6
Problem 3: A charge of 5.60 x 10-3 C is placed at one end of the 8.37 km sandcastle, while an unspecified charge is placed at the opposite end. If the electrical potential energy associated with these charges is -50.5 J, what is the quantity of the second charge?
Solution:
PEelectric = -50.5 J
q2 = 5.60 x 10-3 C
r = 8.37 km = 8.37 x 103 m
kc = 8.99 x 109 Nm2/C2
To find : q1
Equation for the electrical potential energy associated with a pair of charges.
q1 = r PEelectric / kc q2
q1 = (8.36 x 103) (-50.5) / (8.99 x 109) (5.60 x 10-3) C
q1 = 8.40 x 10-3
The quantity of the second charge = 8.40 x 10-3 C.
Problem 4: A potentiometer wire has a length of 1.5 m and a resistance of 10 Ω. It is connected in series with the cell of emf 4 volt and internal resistance 5 Ω. Calculate the potential drop per centimeter of the wire.
Solution:
Given: L = 1.5m, R = 10 Ω, E = 4 V, r = 5 Ω.
K = ER / (R + r) L
K = 4 x 10 / (10 + 5) 1.5
K = 400/225 V/m
K = 400/22500 V/cm = 0.0178 V/cm
The potential drop per centimeter of the wire if 0.0178 V/cm.
FAQs on Charge Flow
Question 1: Copper is a good conductor of electricity. Explain.
Answer:
Copper is a metal and they offer low resistance for the flow of electrons.
Question 2: What is the effect of temperature on the resistance of pure metals?
Answer:
The resistance of pure metals increases with increase in temperature and the resistance decreases with decrease in temperature.
Question 3: What is Electric Charge?
Answer:
The property of subatomic particles that causes it to experience a force when placed in a magnetic field or electric field is known as Electric Charge.
Question 4: Does a moving charge contain an electric field?
Answer:
A moving charge has both electric field and magnetic field. Electric field is associated with the moving charge, but simultaneously a magnetic field is also generated. Only moving charges present inside the conductor can experience this magnetic force.
Share your thoughts in the comments
Please Login to comment...