Find the ratio of LCM to GCD of a given Array
Last Updated :
14 Dec, 2021
Given an array arr[] of positive integers, the task is to find the ratio of LCM and GCD of the given array.
Examples:
Input: arr[] = {2, 3, 5, 9}
Output: 90:1
Explanation:
The GCD of the given array is 1 and the LCM is 90.
Therefore, the ratio is evaluated as 90:1.
Input: arr[] = {6, 12, 36}
Output: 6:1
Explanation:
The GCD of the given array is 6 and the LCM is 36.
Therefore the ratio is evaluated as 6:1.
Approach:
Follow the steps below to solve the problems:
- First of all, we will find the GCD of the given array . For this purpose, we can use the inbuilt function for GCD provided by STL or we can use Euclidean algorithm.
- Then, we will find the LCM of the array by using the below formula:
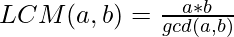
- At last, we will find the required ratio.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findGCD(int arr[], int n)
{
int gcd = arr[0];
for (int i = 1; i < n; i++) {
gcd = __gcd(arr[i], gcd);
if (gcd == 1) {
return 1;
}
}
return gcd;
}
int findLCM(int arr[], int n)
{
int lcm = arr[0];
for (int i = 1; i < n; i++) {
lcm = (((arr[i] * lcm))
/ (__gcd(arr[i], lcm)));
}
return lcm;
}
void findRatio(int arr[], int n)
{
int gcd = findGCD(arr, n);
int lcm = findLCM(arr, n);
cout << lcm / gcd << ":"
<< 1 << endl;
}
int main()
{
int arr[] = { 6, 12, 36 };
int N = sizeof(arr) / sizeof(arr[0]);
findRatio(arr, N);
return 0;
}
|
Java
class GFG{
static int __gcd(int a, int b)
{
if (b == 0)
return a;
return __gcd(b, a % b);
}
static int findGCD(int arr[], int n)
{
int gcd = arr[0];
for (int i = 1; i < n; i++)
{
gcd = __gcd(arr[i], gcd);
if (gcd == 1)
{
return 1;
}
}
return gcd;
}
static int findLCM(int arr[], int n)
{
int lcm = arr[0];
for (int i = 1; i < n; i++)
{
lcm = (((arr[i] * lcm)) /
(__gcd(arr[i], lcm)));
}
return lcm;
}
static void findRatio(int arr[], int n)
{
int gcd = findGCD(arr, n);
int lcm = findLCM(arr, n);
System.out.print((lcm / gcd));
System.out.print(":1");
}
public static void main (String[] args)
{
int arr[] = new int[]{ 6, 12, 36 };
int N = 3;
findRatio(arr, N);
}
}
|
Python3
import math
def findGCD(arr, n):
gcd = arr[0]
for i in range(1, n):
gcd = int(math.gcd(arr[i], gcd))
if (gcd == 1):
return 1
return gcd
def findLCM(arr, n):
lcm = arr[0]
for i in range(1, n):
lcm = int((((arr[i] * lcm)) /
(math.gcd(arr[i], lcm))))
return lcm
def findRatio(arr, n):
gcd = findGCD(arr, n)
lcm = findLCM(arr, n)
print(int(lcm / gcd), ":", "1")
arr = [ 6, 12, 36 ]
N = len(arr)
findRatio(arr, N)
|
C#
using System;
class GFG{
static int __gcd(int a, int b)
{
if (b == 0)
return a;
return __gcd(b, a % b);
}
static int findGCD(int []arr, int n)
{
int gcd = arr[0];
for (int i = 1; i < n; i++)
{
gcd = __gcd(arr[i], gcd);
if (gcd == 1)
{
return 1;
}
}
return gcd;
}
static int findLCM(int []arr, int n)
{
int lcm = arr[0];
for (int i = 1; i < n; i++)
{
lcm = (((arr[i] * lcm)) /
(__gcd(arr[i], lcm)));
}
return lcm;
}
static void findRatio(int []arr, int n)
{
int gcd = findGCD(arr, n);
int lcm = findLCM(arr, n);
Console.Write((lcm / gcd));
Console.Write(":1");
}
public static void Main()
{
int []arr = new int[]{ 6, 12, 36 };
int N = 3;
findRatio(arr, N);
}
}
|
Javascript
<script>
function __gcd(a , b)
{
if (b == 0)
return a;
return __gcd(b, a % b);
}
function findGCD(arr, n)
{
var gcd = arr[0];
for (i = 1; i < n; i++)
{
gcd = __gcd(arr[i], gcd);
if (gcd == 1) {
return 1;
}
}
return gcd;
}
function findLCM(arr, n)
{
var lcm = arr[0];
for (i = 1; i < n; i++)
{
lcm = (((arr[i] * lcm)) / (__gcd(arr[i], lcm)));
}
return lcm;
}
function findRatio(arr , n) {
var gcd = findGCD(arr, n);
var lcm = findLCM(arr, n);
document.write((lcm / gcd));
document.write(":1");
}
var arr = [ 6, 12, 36 ];
var N = 3;
findRatio(arr, N);
</script>
|
Time Complexity: O(N * logN)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...