Find the number of pair of Ideal nodes in a given tree
Last Updated :
05 Oct, 2021
Given a tree of N nodes and an integer K, each node is numbered between 1 and N. The task is to find the number of pairs of ideal nodes in a tree.
A pair of nodes (a, b) is called ideal if
- a is an ancestor of b.
- And, abs(a – b) ? K
Examples:
Input:
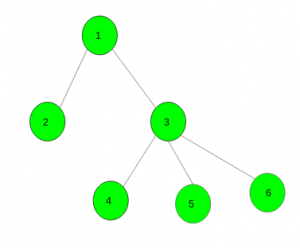
K = 2
Output: 4
(1, 2), (1, 3), (3, 4), (3, 5) are such pairs.
Input: Consider the graph in example 1 and k = 3
Output: 6
(1, 2), (1, 3), (1, 4), (3, 4), (3, 5), (3, 6) are such pairs.
Approach: First, we need to traverse the tree using DFS so we need to find the root node, the node without a parent. As we traverse each node we will store it in a data structure to keep track of all the ancestors for the next node. Before doing that, get the number of the node’s ancestors in the range [presentNode – k, presentNode + k] then add it to the total pairs.
We need a data structure which can:
- Insert a node as we traverse the tree.
- Remove a node as we return.
- Give the number of nodes within the range [presentNode – k, PresentNode + k] which were stored.
Binary indexed tree fulfills the above three operations.
We can do the above 3 operations by initializing all the index values of the BIT to 0 and then:
- Insert a node by updating the index of that node to 1.
- Remove a node by updating the index of that node to 0.
- Get the number of similar pairs of the ancestor of that node by querying for the sum of the range [presentNode – k, PresentNode + k]
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define N 100005
int n, k;
vector<int> al[N];
long long Ideal_pair;
long long bit[N];
bool root_node[N];
long long bit_q(int i, int j)
{
long long sum = 0ll;
while (j > 0) {
sum += bit[j];
j -= (j & (j * -1));
}
i--;
while (i > 0) {
sum -= bit[i];
i -= (i & (i * -1));
}
return sum;
}
void bit_up(int i, long long diff)
{
while (i <= n) {
bit[i] += diff;
i += i & -i;
}
}
void dfs(int node)
{
Ideal_pair += bit_q(max(1, node - k),
min(n, node + k));
bit_up(node, 1);
for (int i = 0; i < al[node].size(); i++)
dfs(al[node][i]);
bit_up(node, -1);
}
void initialise()
{
Ideal_pair = 0;
for (int i = 0; i <= n; i++) {
root_node[i] = true;
bit[i] = 0LL;
}
}
void Add_Edge(int x, int y)
{
al[x].push_back(y);
root_node[y] = false;
}
long long Idealpairs()
{
int r = -1;
for (int i = 1; i <= n; i++)
if (root_node[i]) {
r = i;
break;
}
dfs(r);
return Ideal_pair;
}
int main()
{
n = 6, k = 3;
initialise();
Add_Edge(1, 2);
Add_Edge(1, 3);
Add_Edge(3, 4);
Add_Edge(3, 5);
Add_Edge(3, 6);
cout << Idealpairs();
return 0;
}
|
Java
import java.util.*;
class GFG{
static final int N = 100005;
static int n, k;
@SuppressWarnings("unchecked")
static Vector<Integer> []al = new Vector[N];
static long Ideal_pair;
static long []bit = new long[N];
static boolean []root_node = new boolean[N];
static long bit_q(int i, int j)
{
long sum = 0;
while (j > 0)
{
sum += bit[j];
j -= (j & (j * -1));
}
i--;
while (i > 0)
{
sum -= bit[i];
i -= (i & (i * -1));
}
return sum;
}
static void bit_up(int i, long diff)
{
while (i <= n)
{
bit[i] += diff;
i += i & -i;
}
}
static void dfs(int node)
{
Ideal_pair += bit_q(Math.max(1, node - k),
Math.min(n, node + k));
bit_up(node, 1);
for(int i = 0; i < al[node].size(); i++)
dfs(al[node].get(i));
bit_up(node, -1);
}
static void initialise()
{
Ideal_pair = 0;
for (int i = 0; i <= n; i++) {
root_node[i] = true;
bit[i] = 0;
}
}
static void Add_Edge(int x, int y)
{
al[x].add(y);
root_node[y] = false;
}
static long Idealpairs()
{
int r = -1;
for(int i = 1; i <= n; i++)
if (root_node[i])
{
r = i;
break;
}
dfs(r);
return Ideal_pair;
}
public static void main(String[] args)
{
n = 6;
k = 3;
for(int i = 0; i < al.length; i++)
al[i] = new Vector<Integer>();
initialise();
Add_Edge(1, 2);
Add_Edge(1, 3);
Add_Edge(3, 4);
Add_Edge(3, 5);
Add_Edge(3, 6);
System.out.print(Idealpairs());
}
}
|
Python3
N = 100005
Ideal_pair = 0
al = [[] for i in range(100005)]
bit = [0 for i in range(N)]
root_node = [0 for i in range(N)]
def bit_q(i, j):
sum = 0
while (j > 0):
sum += bit[j]
j -= (j & (j * -1))
i -= 1
while (i > 0):
sum -= bit[i]
i -= (i & (i * -1))
return sum
def bit_up(i, diff):
while (i <= n):
bit[i] += diff
i += i & -i
def dfs(node, x):
Ideal_pair = x
Ideal_pair += bit_q(max(1, node - k),
min(n, node + k))
bit_up(node, 1)
for i in range(len(al[node])):
Ideal_pair = dfs(al[node][i], Ideal_pair)
bit_up(node, -1)
return Ideal_pair
def initialise():
Ideal_pair = 0;
for i in range(n + 1):
root_node[i] = True
bit[i] = 0
def Add_Edge(x, y):
al[x].append(y)
root_node[y] = False
def Idealpairs():
r = -1
for i in range(1, n + 1, 1):
if (root_node[i]):
r = i
break
Ideal_pair = dfs(r, 0)
return Ideal_pair
if __name__ == '__main__':
n = 6
k = 3
initialise()
Add_Edge(1, 2)
Add_Edge(1, 3)
Add_Edge(3, 4)
Add_Edge(3, 5)
Add_Edge(3, 6)
print(Idealpairs())
|
C#
using System;
using System.Collections.Generic;
class GFG{
static readonly int N = 100005;
static int n, k;
static List<int> []al =
new List<int>[N];
static long Ideal_pair;
static long []bit =
new long[N];
static bool []root_node =
new bool[N];
static long bit_q(int i,
int j)
{
long sum = 0;
while (j > 0)
{
sum += bit[j];
j -= (j & (j * -1));
}
i--;
while (i > 0)
{
sum -= bit[i];
i -= (i & (i * -1));
}
return sum;
}
static void bit_up(int i,
long diff)
{
while (i <= n)
{
bit[i] += diff;
i += i & -i;
}
}
static void dfs(int node)
{
Ideal_pair += bit_q(Math.Max(1,
node - k),
Math.Min(n,
node + k));
bit_up(node, 1);
for(int i = 0;
i < al[node].Count; i++)
dfs(al[node][i]);
bit_up(node, -1);
}
static void initialise()
{
Ideal_pair = 0;
for (int i = 0; i <= n; i++)
{
root_node[i] = true;
bit[i] = 0;
}
}
static void Add_Edge(int x,
int y)
{
al[x].Add(y);
root_node[y] = false;
}
static long Idealpairs()
{
int r = -1;
for(int i = 1; i <= n; i++)
if (root_node[i])
{
r = i;
break;
}
dfs(r);
return Ideal_pair;
}
public static void Main(String[] args)
{
n = 6;
k = 3;
for(int i = 0; i < al.Length; i++)
al[i] = new List<int>();
initialise();
Add_Edge(1, 2);
Add_Edge(1, 3);
Add_Edge(3, 4);
Add_Edge(3, 5);
Add_Edge(3, 6);
Console.Write(Idealpairs());
}
}
|
Javascript
<script>
let N = 100005;
let n, k;
let al = new Array(N).fill(0).map((t) => []);
let Ideal_pair;
let bit = new Array(N);
let root_node = new Array(N);
function bit_q(i, j) {
let sum = 0;
while (j > 0) {
sum += bit[j];
j -= (j & (j * -1));
}
i--;
while (i > 0) {
sum -= bit[i];
i -= (i & (i * -1));
}
return sum;
}
function bit_up(i, diff) {
while (i <= n) {
bit[i] += diff;
i += i & -i;
}
}
function dfs(node) {
Ideal_pair += bit_q(Math.max(1, node - k),
Math.min(n, node + k));
bit_up(node, 1);
for (let i = 0; i < al[node].length; i++)
dfs(al[node][i]);
bit_up(node, -1);
}
function initialise() {
Ideal_pair = 0;
for (let i = 0; i <= n; i++) {
root_node[i] = true;
bit[i] = 0;
}
}
function Add_Edge(x, y) {
al[x].push(y);
root_node[y] = false;
}
function Idealpairs() {
let r = -1;
for (let i = 1; i <= n; i++)
if (root_node[i]) {
r = i;
break;
}
dfs(r);
return Ideal_pair;
}
n = 6, k = 3;
initialise();
Add_Edge(1, 2);
Add_Edge(1, 3);
Add_Edge(3, 4);
Add_Edge(3, 5);
Add_Edge(3, 6);
document.write(Idealpairs());
</script>
|
Time Complexity: O(N*log(N))
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...