Find the node whose xor with x gives maximum value
Last Updated :
09 Jun, 2021
Given a tree, and the weights of all the nodes and an integer x, the task is to find a node i such that weight[i] xor x is maximum.
Examples:
Input:
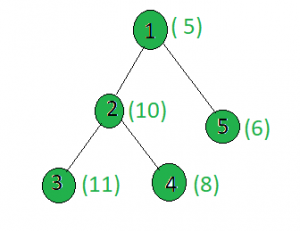
x = 15
Output: 1
Node 1: 5 xor 15 = 10
Node 2: 10 xor 15 = 5
Node 3: 11 xor 15 = 4
Node 4: 8 xor 15 = 7
Node 5: 6 xor 15 = 9
Approach: Perform dfs on the tree and keep track of the node whose weighted xor with x gives the maximum value.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int maximum = INT_MIN, x, ans;
vector<int> graph[100];
vector<int> weight(100);
void dfs(int node, int parent)
{
if (maximum < (weight[node] ^ x)) {
maximum = weight[node] ^ x;
ans = node;
}
for (int to : graph[node]) {
if (to == parent)
continue;
dfs(to, node);
}
}
int main()
{
x = 15;
weight[1] = 5;
weight[2] = 10;
weight[3] = 11;
weight[4] = 8;
weight[5] = 6;
graph[1].push_back(2);
graph[2].push_back(3);
graph[2].push_back(4);
graph[1].push_back(5);
dfs(1, 1);
cout << ans;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int maximum = Integer.MIN_VALUE, x, ans;
@SuppressWarnings("unchecked")
static Vector<Integer>[] graph = new Vector[100];
static int[] weight = new int[100];
static
{
for (int i = 0; i < 100; i++)
graph[i] = new Vector<>();
}
static void dfs(int node, int parent)
{
if (maximum < (weight[node] ^ x))
{
maximum = weight[node] ^ x;
ans = node;
}
for (int to : graph[node])
{
if (to == parent)
continue;
dfs(to, node);
}
}
public static void main(String[] args)
{
x = 15;
weight[1] = 5;
weight[2] = 10;
weight[3] = 11;
weight[4] = 8;
weight[5] = 6;
graph[1].add(2);
graph[2].add(3);
graph[2].add(4);
graph[1].add(5);
dfs(1, 1);
System.out.println(ans);
}
}
|
Python3
import sys
maximum = -sys.maxsize - 1
graph = [[0 for i in range(100)]
for j in range(100)]
weight = [0 for i in range(100)]
ans = []
def dfs(node, parent):
global maximum
if (maximum < (weight[node] ^ x)):
maximum = weight[node] ^ x
ans.append(node)
for to in graph[node]:
if (to == parent):
continue
dfs(to, node)
if __name__ == '__main__':
x = 15
weight[1] = 5
weight[2] = 10
weight[3] = 11
weight[4] = 8
weight[5] = 6
graph[1].append(2)
graph[2].append(3)
graph[2].append(4)
graph[1].append(5)
dfs(1, 1)
print(ans[0])
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int maximum = int.MinValue, x,
ans = int.MaxValue;
static List<List<int>> graph = new List<List<int>>();
static List<int> weight = new List<int>();
static void dfs(int node, int parent)
{
if (maximum < (weight[node] ^ x))
{
maximum = weight[node] ^ x;
ans = node;
}
for (int i = 0; i < graph[node].Count; i++)
{
if (graph[node][i] == parent)
continue;
dfs(graph[node][i], node);
}
}
public static void Main()
{
x = 15;
weight.Add(0);
weight.Add(5);
weight.Add(10);
weight.Add(11);;
weight.Add(8);
weight.Add(6);
for(int i = 0; i < 100; i++)
graph.Add(new List<int>());
graph[1].Add(2);
graph[2].Add(3);
graph[2].Add(4);
graph[1].Add(5);
dfs(1, 1);
Console.Write( ans);
}
}
|
Javascript
<script>
let maximum = Number.MIN_SAFE_INTEGER;
let ans = [];
let graph = new Array();
for(let i = 0; i < 100; i++){
graph.push(new Array().fill(0));
}
let weight = new Array(100).fill(0);
function dfs(node, parent) {
if (maximum < (weight[node] ^ x)) {
maximum = weight[node] ^ x;
ans = node;
}
for (let to of graph[node]) {
if (to == parent)
continue;
dfs(to, node);
}
}
let x = 15;
weight[1] = 5;
weight[2] = 10;
weight[3] = 11;
weight[4] = 8;
weight[5] = 6;
graph[1].push(2);
graph[2].push(3);
graph[2].push(4);
graph[1].push(5);
dfs(1, 1);
document.write(ans);
</script>
|
Complexity Analysis:
- Time Complexity : O(N).
In dfs, every node of the tree is processed once and hence the complexity due to the dfs is O(N) if there are total N nodes in the tree. Therefore, the time complexity is O(N).
- Auxiliary Space : O(1).
Any extra space is not required, so the space complexity is constant.
Share your thoughts in the comments
Please Login to comment...