Find the lexicographically largest palindromic Subsequence of a String
Last Updated :
15 Sep, 2022
Given a string 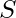 . The task is to find the lexicographically largest subsequence of the string which is a palindrome.
. The task is to find the lexicographically largest subsequence of the string which is a palindrome.
Examples:
Input : str = "abrakadabra"
Output : rr
Input : str = "geeksforgeeks"
Output : ss
The idea is to observe a character a is said to be lexicographically larger than a character b if it’s ASCII value is greater than that of b.
Since the string has to be palindromic, the string should contain the largest characters only, as if we place any other smaller character in between the first and last character then it will make the string lexicographically smaller.
To find the lexicographically largest subsequence, first find the largest characters in the given string and append all of its occurrences in the original string to form the resultant subsequence string.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
string largestPalinSub(string s)
{
string res;
char mx = s[0];
for (int i = 1; i < s.length(); i++)
mx = max(mx, s[i]);
for (int i = 0; i < s.length(); i++)
if (s[i] == mx)
res += s[i];
return res;
}
int main()
{
string s = "geeksforgeeks";
cout << largestPalinSub(s);
}
|
Java
class GFG
{
static String largestPalinSub(String s)
{
String res = "";
char mx = s.charAt(0);
for (int i = 1; i < s.length(); i++)
mx = (char)Math.max((int)mx,
(int)s.charAt(i));
for (int i = 0; i < s.length(); i++)
if (s.charAt(i) == mx)
res += s.charAt(i);
return res;
}
public static void main(String []args)
{
String s = "geeksforgeeks";
System.out.println(largestPalinSub(s));
}
}
|
Python3
def largestPalinSub(s):
res = ""
mx = s[0]
for i in range(1, len(s)):
mx = max(mx, s[i])
for i in range(0, len(s)):
if s[i] == mx:
res += s[i]
return res
if __name__ == "__main__":
s = "geeksforgeeks"
print(largestPalinSub(s))
|
C#
using System;
class GFG
{
static string largestPalinSub(string s)
{
string res = "";
char mx = s[0];
for (int i = 1; i < s.Length; i++)
mx = (char)Math.Max((int)mx,
(int)s[i]);
for (int i = 0; i < s.Length; i++)
if (s[i] == mx)
res += s[i];
return res;
}
public static void Main()
{
string s = "geeksforgeeks";
Console.WriteLine(largestPalinSub(s));
}
}
|
PHP
<?php
function largestPalinSub($s)
{
$res="";
$mx = $s[0];
for ($i = 1; $i < strlen($s); $i++)
{
$mx = max($mx, $s[$i]);
}
for ($i = 0; $i < strlen($s); $i++)
{
if ($s[$i] == $mx)
{
$res.=$s[$i];
}
}
return $res;
}
$s = "geeksforgeeks";
echo(largestPalinSub($s));
?>
|
Javascript
<script>
function largestPalinSub(s)
{
let res = "";
let mx = s[0];
for (let i = 1; i < s.length; i++)
mx = String.fromCharCode(Math.max(mx.charCodeAt(),
s[i].charCodeAt()));
for (let i = 0; i < s.length; i++)
if (s[i] == mx)
res += s[i];
return res;
}
let s = "geeksforgeeks";
document.write(largestPalinSub(s));
</script>
|
Complexity Analysis:
- Time Complexity: O(N), where N is the length of the string.
- Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...