Sum of series M/1 + (M+P)/2 + (M+2*P)/4 + (M+3*P)/8……up to infinite
Last Updated :
20 Feb, 2023
Find the sum of series M/1 + (M+P)/2 + (M+2*P)/4 + (M+3*P)/8……up to infinite where M and P are positive integers.
Examples:
Input : M = 0, P = 3;
Output : 6
Input : M = 2, P = 9;
Output : 22
Method :
S = M/1 + (M + P)/2 + (M + 2*P)/4 + (M + 3*P) / 8……up to infinite
so the solution of this series will be like this
we are going to divide this series into two parts-
S = (M/1 + M/2 + M/4 + M/8……up to infinite) + ( p/2 + (2*p)/4 + (3*p)/8 + ….up to infinite)
let us consider it
S = A + B ……..eq(1)
where,
A = M/1 + M/2 + M/4 + M/8……up to infinite
A = M*(1 + 1/2 + 1/4 + 1/8….up to infinite)
which is G.P of infinite terms with r = 1/2;
According to the formula of G.P sum of infinite terms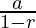 for r < 1 and
for r < 1 and
a is first term and r is common ratio so now,
A = M * ( 1 / (1 – 1/2) )
A = 2 * M ;
Now for B –
B = ( p/2 + (2*p)/4 + (3*p)/8 + ….up to infinite)
B = P/2 * ( 1 + 2*(1/2) + 3*(1/4) + ……up to infinite)
it is sum of AGP of infinite terms with a = 1, r = 1/2 and d = 1;
According to the formula 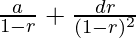 where a is first term,
where a is first term,
r is common ratio and d is common difference so now,
B = P/2 * ( 1 / (1-1/2) + (1*1/2) / (1-1/2)^2 )
B = P/2 * 4
B = 2*P ;
put value of A and B in eq(1)
S = 2(M + P)
C++
#include <iostream>
using namespace std;
int sum(int M, int P)
{
return 2*(M + P);
}
int main() {
int M = 2, P = 9;
cout << sum(M,P);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int sum_series(int M, int P)
{
return 2 * (M + P);
}
public static void main (String[] args)
{
int M = 2;
int P = 9;
System.out.println( sum_series(M, P)) ;
}
}
|
Python3
def sum_series(M, P):
return int(2 * (M + P))
M = 2
P = 9
print(sum_series(M ,P))
|
C#
using System;
class GFG {
static int sum_series(int M, int P)
{
return 2*(M + P);
}
public static void Main ()
{
int M =2;
int P =9;
Console.Write( sum_series(M,P)) ;
}
}
|
PHP
<?php
function sum($M, $P)
{
return 2*($M + $P);
}
$M = 2;
$P = 9;
echo sum($M, $P);
?>
|
Javascript
<script>
function sum_series(M, P)
{
return 2 * (M + P);
}
let M = 2;
let P = 9;
document.write( sum_series(M, P));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...