Find number of path with same moves in full Binary Tree
Last Updated :
23 Mar, 2024
Consider a Binary Tree having N nodes having root equal to 1. In which for any node X, the left and right child are 2*X and ((2*X) + 1). Then in such a Binary Tree, there can be four possible moves:
- From parent node to left child node (Let us name this move as BL, which means Bottom Left)
- From parent node to right child node (Let us name this move as BR, which means Bottom Right)
- From left child node to parent node (Let us name this move as UR, which means Up Right)
- From right child node to parent node (Let us name this move UL, which means Up Left)
You are given two integers A and B. Then your task is to count the number of pairs of nodes having the same path moves as A and B have.
Examples:
Input: N = 11, A = 9, B = 11
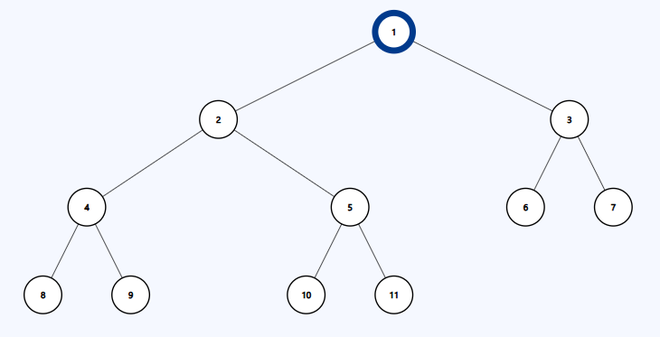
Input Tree having root node as 1
Output: 2
Explanation: There are two pair of nodes which have same path moves. (5, 7) and (9, 11). For more clarification see below.
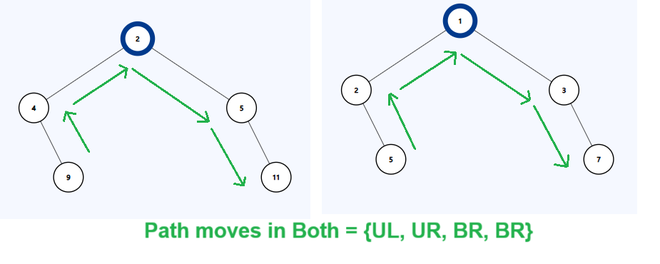
Explanation of Test case 1
- Path from Node 9 to 11: Let us start the path from 9.
- From 9 to 4 as right child to parent: UL
- From 4 to 2 as left child to parent: UR
- From 2 to 5 as parent to right child: BR
- From 5 to 11 as parent to right child: BR
- The path moves will be: {UL, UR, BR, BR}
- Path from Node 5 to 7: Let us start the path from 5.
- From 5 to 2 as right child to parent: UL
- From 2 to 1 as left child to parent: UR
- From 1 to 3 as parent to right child: BR
- From 3 to 7 as parent to right child: BR
- The path moves will be: {UL, UR, BR, BR}
It can be verified that (5, 7) and (9, 11) are the only pairs having the same path moves as A = 9 and B = 11.
Input: N = 10, A = 1, B = 1
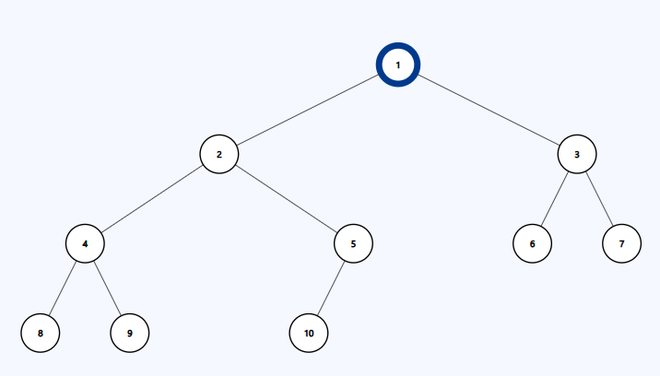
Input tree of Test case 2
Output: 10
Explanation: Going from (1, 1) requires no moves. Hence, there are 10 such pairs, which are: (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (7, 7), (8, 8), (9, 9) and (10, 10). Therefore, output is 10.
Approach: Implement the idea below to solve the problem
The problem is based on the LCA (Lowest Common Ancestor) approach. Let us discuss the different approaches for solving the problem. We will see 3 approaches for solving the problem, having different Time and Space Complexities.
Here’s a brief explanation of the approach used for this approach:
- Main Idea: The code used or this approach builds paths from two given nodes to the root of the binary tree. This is done by repeatedly dividing the node values by 2 until they become equal, which signifies reaching their Lowest Common Ancestor.
- Significance of Stacks: In Stacks path is stored as a stack of integers. Where each integer represents a move to the left child (if it’s 2) or to the right child (if it’s 1). Stacks are used because they provide an efficient way to store and retrieve the path information in a Last-In-First-Out (LIFO) manner.
- Calculating Ranges: After building the paths, the code calculates the range of nodes that can be reached from each node without visiting any node more than once. This is done by iterating over the moves stored in the stacks and updating the range accordingly.
- Counting pairs: Finally, it counts how many nodes within a certain range can be reached from each node. This is done by calculating how many multiples of “diffx” and “diffy” (the sizes of the ranges) fit into [1, N].
- Results: The minimum of these two counts is then printed as the result. This approach ensures that each node is visited at most once, making it an efficient solution.
Steps were taken to solve the problem:
- Build Paths to Root:
- Create two stacks let say StackX and StackY, to store the paths from A and B to the root of the binary tree.
- While (A != B):
- If A is greater than B, update A and push the corresponding direction (1 for right, 2 for left) onto StackX.
- If B is greater than A, update B and push the corresponding direction onto StackY.
- Initialize Node Ranges:
- Initialize the ranges of nodes that can be reached from x and y (xx1, xx2, yy1, yy2).
- Calculate Ranges from Paths:
- Use the Stacks to calculate the ranges of nodes that can be reached from A and B.
- Pop elements from the stacks and update the ranges accordingly.
- Calculate Size of Ranges:
- Calculate the size of each range as diffx and diffy.
- Count Reachable Nodes:
- Calculate how many nodes within the range [1, N] can be reached from A and B (cc1 and cc2).
- Output the result as: (min(cc1, cc2) + 1)
Code to implement the approach:
C++
#include <cmath>
#include <iostream>
#include <stack>
using namespace std;
// Method to count pairs
void Count_pairs(int n, int x, int y)
{
// Create two stacks to store the paths from x and y to
// the root
stack<int> stackx;
stack<int> stacky;
// Build the paths from x and y to the root
while (x != y) {
if (x > y) {
if (x % 2 == 0) {
x = x / 2;
stackx.push(2); // Move to the left child
}
else {
x = (x - 1) / 2;
stackx.push(1); // Move to the right child
}
}
else {
if (y % 2 == 0) {
y = y / 2;
stacky.push(2); // Move to the left child
}
else {
y = (y - 1) / 2;
stacky.push(1); // Move to the right child
}
}
}
// Initialize the ranges of nodes that can be reached
// from x and y
int xx1 = 1, xx2 = 2;
int yy1 = 1, yy2 = 2;
// Calculate the range of nodes that can be reached from
// x
while (!stackx.empty()) {
int ss = stackx.top();
stackx.pop();
if (ss == 2) {
xx1 = xx1 * 2; // Move to the left child
xx2 = xx2 * 2; // Move to the left child
}
else {
// Move to the right child
xx1 = xx1 * 2 + 1;
// Move to the right child
xx2 = xx2 * 2 + 1;
}
}
// Calculate the range of nodes that can be reached from
// y
while (!stacky.empty()) {
int ff = stacky.top();
stacky.pop();
if (ff == 2) {
// Move to the left child
yy1 = yy1 * 2;
// Move to the left child
yy2 = yy2 * 2;
}
else {
// Move to the right child
yy1 = yy1 * 2 + 1;
// Move to the right child
yy2 = yy2 * 2 + 1;
}
}
// Calculate the size of each range
int diffx = xx2 - xx1;
int diffy = yy2 - yy1;
// Count how many nodes within [1, n] can be reached
// from x and y
int cc1 = floor((n - xx1) / diffx);
int cc2 = floor((n - yy1) / diffy);
// Print the minimum count as the result
cout << min(cc1, cc2) + 1 << endl;
}
int main()
{
// Initialize the values of n, x, and y
int n = 11;
int a = 9;
int b = 11;
// Function call
Count_pairs(n, a, b);
return 0;
}
// Java code to implement the approach
import java.util.*;
// Driver Class
class GFG {
// Driver Function
public static void main(String[] args)
{
// Initialize the values of n, x, and y
int n = 11;
int a = 9;
int b = 11;
// Function call
Count_pairs(n, a, b);
}
// Method to count pairs
public static void Count_pairs(int n, int x, int y)
{
// Create two stacks to store the paths from x and y
// to the root
Stack<Integer> stackx = new Stack<>();
Stack<Integer> stacky = new Stack<>();
// Build the paths from x and y to the root
while (x != y) {
if (x > y) {
if (x % 2 == 0) {
x = x / 2;
stackx.push(
2); // Move to the left child
}
else {
x = (x - 1) / 2;
stackx.push(
1); // Move to the right child
}
}
else {
if (y % 2 == 0) {
y = y / 2;
stacky.push(
2); // Move to the left child
}
else {
y = (y - 1) / 2;
stacky.push(
1); // Move to the right child
}
}
}
// Initialize the ranges of nodes that can be
// reached from x and y
int xx1 = 1, xx2 = 2;
int yy1 = 1, yy2 = 2;
// Calculate the range of nodes that can be reached
// from x
while (!stackx.isEmpty()) {
int ss = stackx.pop();
if (ss == 2) {
xx1 = xx1 * 2; // Move to the left child
xx2 = xx2 * 2; // Move to the left child
}
else {
// Move to the right child
xx1 = xx1 * 2 + 1;
// Move to the right child
xx2 = xx2 * 2 + 1;
}
}
// Calculate the range of nodes
// that can be reached from y
while (!stacky.isEmpty()) {
int ff = stacky.pop();
if (ff == 2) {
// Move to the left child
yy1 = yy1 * 2;
// Move to the left child
yy2 = yy2 * 2;
}
else {
// Move to the right child
yy1 = yy1 * 2 + 1;
// Move to the right child
yy2 = yy2 * 2 + 1;
}
}
// Calculate the size of each range
int diffx = xx2 - xx1;
int diffy = yy2 - yy1;
// Count how many nodes within [1, n]
// can be reached from x and y
int cc1 = (int)Math.floor((n - xx1) / diffx);
int cc2 = (int)Math.floor((n - yy1) / diffy);
// Print the minimum count
// as the result
System.out.println(Math.min(cc1, cc2) + 1);
}
}
using System;
using System.Collections.Generic;
class MainClass
{
// Method to count pairs
static void CountPairs(int n, int x, int y)
{
// Create two stacks to store the paths from x and y to
// the root
Stack<int> stackx = new Stack<int>();
Stack<int> stacky = new Stack<int>();
// Build the paths from x and y to the root
while (x != y)
{
if (x > y)
{
if (x % 2 == 0)
{
x = x / 2;
stackx.Push(2); // Move to the left child
}
else
{
x = (x - 1) / 2;
stackx.Push(1); // Move to the right child
}
}
else
{
if (y % 2 == 0)
{
y = y / 2;
stacky.Push(2); // Move to the left child
}
else
{
y = (y - 1) / 2;
stacky.Push(1); // Move to the right child
}
}
}
// Initialize the ranges of nodes that can be reached
// from x and y
int xx1 = 1, xx2 = 2;
int yy1 = 1, yy2 = 2;
// Calculate the range of nodes that can be reached from
// x
while (stackx.Count > 0)
{
int ss = stackx.Pop();
if (ss == 2)
{
xx1 = xx1 * 2; // Move to the left child
xx2 = xx2 * 2; // Move to the left child
}
else
{
// Move to the right child
xx1 = xx1 * 2 + 1;
// Move to the right child
xx2 = xx2 * 2 + 1;
}
}
// Calculate the range of nodes that can be reached from
// y
while (stacky.Count > 0)
{
int ff = stacky.Pop();
if (ff == 2)
{
// Move to the left child
yy1 = yy1 * 2;
// Move to the left child
yy2 = yy2 * 2;
}
else
{
// Move to the right child
yy1 = yy1 * 2 + 1;
// Move to the right child
yy2 = yy2 * 2 + 1;
}
}
// Calculate the size of each range
int diffx = xx2 - xx1;
int diffy = yy2 - yy1;
// Count how many nodes within [1, n] can be reached
// from x and y
int cc1 = (int)Math.Floor((double)(n - xx1) / diffx);
int cc2 = (int)Math.Floor((double)(n - yy1) / diffy);
// Print the minimum count as the result
Console.WriteLine(Math.Min(cc1, cc2) + 1);
}
public static void Main(string[] args)
{
// Initialize the values of n, x, and y
int n = 11;
int a = 9;
int b = 11;
// Function call
CountPairs(n, a, b);
}
}
// JavaScript code for the above approach:
// Function to count pairs
function countPairs(n, x, y) {
// Create two stacks to store the paths
// from x and y to the root
const stackx = [];
const stacky = [];
// Build the paths from x and y to the root
while (x !== y) {
if (x > y) {
if (x % 2 === 0) {
x = x / 2;
stackx.push(2); // Move to the left child
} else {
x = (x - 1) / 2;
stackx.push(1); // Move to the right child
}
} else {
if (y % 2 === 0) {
y = y / 2;
stacky.push(2); // Move to the left child
} else {
y = (y - 1) / 2;
stacky.push(1); // Move to the right child
}
}
}
// Initialize the ranges of nodes that can
// be reached from x and y
let xx1 = 1, xx2 = 2;
let yy1 = 1, yy2 = 2;
// Calculate the range of nodes that can
// be reached from x
while (stackx.length > 0) {
const ss = stackx.pop();
if (ss === 2) {
xx1 *= 2; // Move to the left child
xx2 *= 2; // Move to the left child
} else {
xx1 = xx1 * 2 + 1; // Move to the right child
xx2 = xx2 * 2 + 1; // Move to the right child
}
}
// Calculate the range of nodes that can
// be reached from y
while (stacky.length > 0) {
const ff = stacky.pop();
if (ff === 2) {
yy1 *= 2; // Move to the left child
yy2 *= 2; // Move to the left child
} else {
yy1 = yy1 * 2 + 1; // Move to the right child
yy2 = yy2 * 2 + 1; // Move to the right child
}
}
// Calculate the size of each range
const diffx = xx2 - xx1;
const diffy = yy2 - yy1;
// Count how many nodes within [1, n] can be
// reached from x and y
const cc1 = Math.floor((n - xx1) / diffx);
const cc2 = Math.floor((n - yy1) / diffy);
// Print the minimum count as the result
console.log(Math.min(cc1, cc2) + 1);
}
// Initialize the values of n, x, and y
const n = 11;
let x = 9;
let y = 11;
// Function call
countPairs(n, x, y);
# Python Implementation
import math
def count_pairs(n, x, y):
stackx = []
stacky = []
while x != y:
if x > y:
if x % 2 == 0:
x = x // 2
stackx.append(2) # Move to the left child
else:
x = (x - 1) // 2
stackx.append(1) # Move to the right child
else:
if y % 2 == 0:
y = y // 2
stacky.append(2) # Move to the left child
else:
y = (y - 1) // 2
stacky.append(1) # Move to the right child
xx1, xx2 = 1, 2
yy1, yy2 = 1, 2
while stackx:
ss = stackx.pop()
if ss == 2:
xx1 = xx1 * 2 # Move to the left child
xx2 = xx2 * 2 # Move to the left child
else:
xx1 = xx1 * 2 + 1 # Move to the right child
xx2 = xx2 * 2 + 1 # Move to the right child
while stacky:
ff = stacky.pop()
if ff == 2:
yy1 = yy1 * 2 # Move to the left child
yy2 = yy2 * 2 # Move to the left child
else:
yy1 = yy1 * 2 + 1 # Move to the right child
yy2 = yy2 * 2 + 1 # Move to the right child
diffx = xx2 - xx1
diffy = yy2 - yy1
cc1 = math.floor((n - xx1) / diffx)
cc2 = math.floor((n - yy1) / diffy)
return min(cc1, cc2) + 1
n = 11
a = 9
b = 11
result = count_pairs(n, a, b)
print(result)
# This code is contributed by Sakshi
Complexity Analysis:
Time Complexity: {O(log(max(A, B))) + O(log(N))}, As the while loop runs until A is equal to B. Therefore, the time complexity of this part is O(log(max(A, B))). The subsequent while loops that calculate the ranges from A and B pop elements from the stacks and perform constant-time operations for each element. The size of the stacks is limited by the height of the binary tree, which is O(log(N)) in the worst case. Therefore, total complexity is: {O(log(max(A, B))) + O(log(B))}
Auxiliary Space: O(logN), As Two stacks, StackX and StackY, are used to store the paths from A and B to the root. The size of these stacks is at most O(log(n)) in the worst case, as it is limited by the height of the binary tree.
Approach 2 (Space Optimized):
- Building Paths: This step is the same as previous approach. In this approach builds paths from two given nodes to the root of the binary tree. This is done by repeatedly dividing the node values by 2 until they become equal, which signifies reaching their Lowest Common Ancestor.
- Use of Strings: The path is stored as a string of characters, where each character represents a move to the left child (if it’s ‘0’) or to the right child (if it’s ‘1’). Strings are used because they provide an efficient way to store and retrieve the path information.
- Calculating Ranges: After building the paths, the code calculates the range of nodes that can be reached from each node without visiting any node more than once. This is done by iterating over the characters stored in the strings and updating the range accordingly.
- Counting Nodes: This step is also similar to previous approach. Finally, it counts how many nodes within a certain range can be reached from each node. This is done by calculating how many multiples of m (the size of the range) fit into [1, N].
- Result: The minimum of these two counts is then printed as the result.
Steps were taken to solve the problem:
- Determine Path:
- Create two empty strings let say pathA and pathB.
- Use a while loop to determine the binary path for A and B from the root.
- In each iteration, compare A and B, and update the corresponding path.
- Calculate Maximum Depth:
- Initialize maxDepth to N.
- Use a for loop to calculate the maximum depth by dividing it by 2 for the length of the longest path.
- Check Path:
- Define a function let say CheckPath() that takes a path, current depth, and N as parameters.
- In this function, use a loop to traverse the path configuration and update a pointer.
- Check if the pointer exceeds the N at the current depth.
- Result:
- Calculate the result by subtracting the maximum of the path configuration checks from the maximum depth.
Code to implement the approach:
C++
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
// Function to check if the path configuration exceeds the tree size at a certain depth
int checkPath(string path, long long currentDepth, long long N) {
long long pointer = currentDepth;
for (int j = 0; j < path.length(); j++) {
pointer = pointer * 2 + (path[j] - '0');
}
// Check if the pointer exceeds the tree size
if (pointer > N)
return 1;
return 0;
}
// Method to print number of pairs of node
void Count_pairs(long long N, long long A, long long B) {
// Find the parent of (nodeA, nodeB)
// and path configuration for nodeA,
// nodeB from LCA
string pathA = "";
string pathB = "";
// Determine path configuration for
// nodeA and nodeB from LCA
while (A != B) {
if (A > B) {
if (A % 2 == 0)
pathA = '0' + pathA;
else
pathA = '1' + pathA;
A = A / 2;
} else {
if (B % 2 == 0)
pathB = '0' + pathB;
else
pathB = '1' + pathB;
B = B / 2;
}
}
// Calculate the maximum depth of
// the common path configuration
long long maxDepth = N;
for (int i = 0; i < max(pathA.length(), pathB.length()); i++) {
maxDepth = maxDepth / 2;
}
// Output the result (maximum depth
// - maximum of path configuration checks)
cout << (maxDepth - max(checkPath(pathA, maxDepth, N), checkPath(pathB, maxDepth, N))) << endl;
}
// Driver Function
int main() {
// Input: Size of the binary tree
// and nodes to compare
long long N = 10;
long long A = 1;
long long B = 1;
// Function call
Count_pairs(N, A, B);
return 0;
}
import java.util.Scanner;
public class Main {
// Function to check if the path configuration exceeds the tree size at a certain depth
static int checkPath(String path, long currentDepth, long N) {
long pointer = currentDepth;
for (int j = 0; j < path.length(); j++) {
pointer = pointer * 2 + (path.charAt(j) - '0');
}
// Check if the pointer exceeds the tree size
if (pointer > N)
return 1;
return 0;
}
// Method to print number of pairs of node
static void countPairs(long N, long A, long B) {
// Find the parent of (nodeA, nodeB)
// and path configuration for nodeA,
// nodeB from LCA
StringBuilder pathA = new StringBuilder();
StringBuilder pathB = new StringBuilder();
// Determine path configuration for
// nodeA and nodeB from LCA
while (A != B) {
if (A > B) {
if (A % 2 == 0)
pathA.insert(0, '0');
else
pathA.insert(0, '1');
A = A / 2;
} else {
if (B % 2 == 0)
pathB.insert(0, '0');
else
pathB.insert(0, '1');
B = B / 2;
}
}
// Calculate the maximum depth of
// the common path configuration
long maxDepth = N;
for (int i = 0; i < Math.max(pathA.length(), pathB.length()); i++) {
maxDepth = maxDepth / 2;
}
// Output the result (maximum depth
// - maximum of path configuration checks)
System.out.println(maxDepth - Math.max(checkPath(pathA.toString(), maxDepth, N),
checkPath(pathB.toString(), maxDepth, N)));
}
// Driver Function
public static void main(String[] args) {
// Input: Size of the binary tree
// and nodes to compare
long N = 10;
long A = 1;
long B = 1;
// Function call
countPairs(N, A, B);
}
}
// C# program for the above approach
using System;
public class GFG {
// Function to check if the path configuration exceeds
// the tree size at a certain depth
static int CheckPath(string path, long currentDepth,
long N)
{
long pointer = currentDepth;
for (int j = 0; j < path.Length; j++) {
pointer = pointer * 2 + (path[j] - '0');
}
// Check if the pointer exceeds the tree size
if (pointer > N)
return 1;
return 0;
}
// Method to print number of pairs of node
static void CountPairs(long N, long A, long B)
{
// Find the parent of (nodeA, nodeB)
// and path configuration for nodeA,
// nodeB from LCA
string pathA = "";
string pathB = "";
// Determine path configuration for
// nodeA and nodeB from LCA
while (A != B) {
if (A > B) {
if (A % 2 == 0)
pathA = '0' + pathA;
else
pathA = '1' + pathA;
A = A / 2;
}
else {
if (B % 2 == 0)
pathB = '0' + pathB;
else
pathB = '1' + pathB;
B = B / 2;
}
}
// Calculate the maximum depth of
// the common path configuration
long maxDepth = N;
for (int i = 0;
i < Math.Max(pathA.Length, pathB.Length);
i++) {
maxDepth = maxDepth / 2;
}
// Output the result (maximum depth
// - maximum of path configuration checks)
Console.WriteLine(
maxDepth
- Math.Max(CheckPath(pathA, maxDepth, N),
CheckPath(pathB, maxDepth, N)));
}
// Driver Function
public static void Main(string[] args)
{
// Input: Size of the binary tree
// and nodes to compare
long N = 10;
long A = 1;
long B = 1;
// Function call
CountPairs(N, A, B);
}
}
// This code is contributed by Susobhan Akhuli
// Function to check if the path configuration exceeds the tree size at a certain depth
function checkPath(path, currentDepth, N) {
let pointer = currentDepth;
for (let j = 0; j < path.length; j++) {
pointer = pointer * 2 + parseInt(path[j]);
}
// Check if the pointer exceeds the tree size
return pointer > N ? 1 : 0;
}
// Method to print the number of pairs of nodes
function countPairs(N, A, B) {
// Find the parent of (nodeA, nodeB) and path configuration for nodeA, nodeB from LCA
let pathA = "";
let pathB = "";
// Determine path configuration for nodeA and nodeB from LCA
while (A !== B) {
if (A > B) {
pathA = (A % 2 === 0 ? '0' : '1') + pathA;
A = Math.floor(A / 2);
} else {
pathB = (B % 2 === 0 ? '0' : '1') + pathB;
B = Math.floor(B / 2);
}
}
// Calculate the maximum depth of the common path configuration
let maxDepth = N;
for (let i = 0; i < Math.max(pathA.length, pathB.length); i++) {
maxDepth = Math.floor(maxDepth / 2);
}
// Output the result (maximum depth - maximum of path configuration checks)
console.log(maxDepth - Math.max(checkPath(pathA, maxDepth, N), checkPath(pathB, maxDepth, N)));
}
// Driver Function
function main() {
// Input: Size of the binary tree and nodes to compare
let N = 10;
let A = 1;
let B = 1;
// Function call
countPairs(N, A, B);
}
// Run the main function
main();
# Function to check if the path configuration exceeds the tree size at a certain depth
def check_path(path, current_depth, N):
pointer = current_depth
for j in range(len(path)):
pointer = pointer * 2 + int(path[j])
# Check if the pointer exceeds the tree size
if pointer > N:
return 1
return 0
# Method to print the number of pairs of nodes
def count_pairs(N, A, B):
# Find the parent of (nodeA, nodeB)
# and path configuration for nodeA,
# nodeB from LCA
pathA = ""
pathB = ""
# Determine path configuration for
# nodeA and nodeB from LCA
while A != B:
if A > B:
if A % 2 == 0:
pathA = '0' + pathA
else:
pathA = '1' + pathA
A = A // 2
else:
if B % 2 == 0:
pathB = '0' + pathB
else:
pathB = '1' + pathB
B = B // 2
# Calculate the maximum depth of
# the common path configuration
max_depth = N
for i in range(max(len(pathA), len(pathB))):
max_depth = max_depth // 2
# Output the result (maximum depth
# - maximum of path configuration checks)
print(max_depth - max(check_path(pathA, max_depth, N), check_path(pathB, max_depth, N)))
# Driver Function
if __name__ == "__main__":
# Input: Size of the binary tree
# and nodes to compare
N = 10
A = 1
B = 1
# Function call
count_pairs(N, A, B)
Time Complexity: O(log(max(A, B)))
Auxiliary Space: O(log(max(A, B))). Which is the space required for path by strings.
This approach uses Bitwise and Binary Search concept for solving the problem. Let’s break down the approach step by step:
- Binary Representation Adjustment:
- The binary representations of A and B are obtained and adjusted to align with the LCA. The adjusted binary representations are converted back to decimal as x1 and x2. and the lengths of the adjusted representations are stored in s1 and s2.
- Binary Search Algorithm:
- The approach uses a binary search algorithm to find the maximum depth (lo) such that the adjusted binary representations of A and B (shifted by s1 and s2 bits, respectively) can be combined to form valid nodes within the binary tree.
- The binary search is performed on the range from the LCA (g) to the size of the tree (N). The conditions for a valid combination involve checking if the combined values (x and y) are within the range of valid nodes in the binary tree.
- LCA Function:
- The LCA() function implements a bitwise method to find the Lowest Common Ancestor of A and B in a binary tree. It uses bitwise operations to iteratively reduce both A and B until they have the same highest one-bit.
- Results:
- The result of the binary search (lo) represents the maximum depth at which the path of nodes A and B are the same.
- Complexity:
- The time complexity of the binary search is O(log n), where N is the size of the binary tree.
- The LCA function has a time complexity proportional to the number of bits in the larger of A or B.
This approach efficiently finds the maximum depth at which the path of nodes A and B are the same in a binary tree using a binary search algorithm and bitwise operations for LCA calculation.
Steps were taken to solve the problem:
- Find Lowest Common Ancestor (LCA):
- Use the findLCA() function to find the Lowest Common Ancestor let say lca of A and B.
- Convert to Binary:
- Convert A, B, and LCA of both to their binary representations, name them as A_binary, B_binary, lca_binary.
- Adjust Binary Representations:
- Adjust the binary representations of A and B by removing the common bits with the lca binary.
- Convert Back to Decimal:
- Convert the adjusted binary representations of A and B back to decimal in adjustedABinary and adjustedBBinary respectively.
- Binary Search Algorithm:
- Use a binary search algorithm to find the maximum depth.
- Iterate until low is not less than high, updating low and high based on binary operations.
- Result:
- Output the maximum depth.
Code to implement the approach:
C++
// CPP program for the above approach
#include <bitset>
#include <iostream>
using namespace std;
// Function to find the Lowest Common Ancestor (LCA) of two
// numbers A and B in a Binary Tree
long findLCA(long A, long B)
{
while (B > A)
B >>= 1;
while (A > B)
A >>= 1;
while (A != B) {
A >>= 1;
B >>= 1;
}
return A;
}
// Method to output the number of pairs
void Count_pairs(long n, long u, long v)
{
// Finding the Lowest Common Ancestor (LCA) of u and v
long lca = findLCA(u, v);
string lcaBinaryRepresentation
= bitset<64>(lca).to_string();
// Getting the binary representations of u and v
string uBinaryRepresentation
= bitset<64>(u).to_string();
string vBinaryRepresentation
= bitset<64>(v).to_string();
// Adjusting binary representations to align with the
// LCA
int lcaLength = lcaBinaryRepresentation.length();
uBinaryRepresentation = uBinaryRepresentation.substr(
uBinaryRepresentation.length() - lcaLength);
vBinaryRepresentation = vBinaryRepresentation.substr(
vBinaryRepresentation.length() - lcaLength);
// Converting adjusted binary representations back to
// decimal
long adjustedUBinary
= uBinaryRepresentation.empty()
? 0
: stoll(uBinaryRepresentation, nullptr, 2);
long adjustedVBinary
= vBinaryRepresentation.empty()
? 0
: stoll(vBinaryRepresentation, nullptr, 2);
// Binary Search algorithm to find the maximum depth
long lo = lca, hi = n;
while (lo < hi) {
long mid = (lo + hi + 1) / 2;
long x = (mid << lcaLength) | adjustedUBinary;
long y = (mid << lcaLength) | adjustedVBinary;
// Checking if the combined values are within the
// range of valid nodes
if (x <= n && y <= n) {
lo = mid;
}
else {
hi = mid - 1;
}
}
// Printing the result (maximum depth)
cout << lo << endl;
}
// Driver Function
int main()
{
// Inputs
long N = 8;
long A = 1;
long B = 8;
// Function call
Count_pairs(N, A, B);
return 0;
}
// This code is contributed by Susobhan Akhuli
// Java code to implement the approach
import java.io.*;
import java.util.*;
// Driver Class
public class Main {
// Driver Function
public static void main(String[] args)
{
// Inputs
long N = 8;
long A = 1;
long B = 8;
// Function call
Count_pairs(N, A, B);
}
// Method to output the number of pairs
public static void Count_pairs(long n, long u, long v)
{
// Finding the Lowest Common Ancestor
// (LCA) of u and v
long lca = findLCA(u, v);
String lcaBinaryRepresentation
= Long.toString(lca, 2);
// Getting the binary representations
// of u and v
String uBinaryRepresentation = Long.toString(u, 2);
String vBinaryRepresentation = Long.toString(v, 2);
// Adjusting binary representations
// to align with the LCA
uBinaryRepresentation
= uBinaryRepresentation.substring(
lcaBinaryRepresentation.length());
vBinaryRepresentation
= vBinaryRepresentation.substring(
lcaBinaryRepresentation.length());
// Converting adjusted binary
// representations back to decimal
long adjustedUBinary
= uBinaryRepresentation.length() == 0
? 0
: Long.parseLong(uBinaryRepresentation,
2);
long adjustedVBinary
= vBinaryRepresentation.length() == 0
? 0
: Long.parseLong(vBinaryRepresentation,
2);
// Storing lengths of adjusted binary
// representations
long uBinaryLength = uBinaryRepresentation.length();
long vBinaryLength = vBinaryRepresentation.length();
// Binary Search algorithm to find
// the maximum depth
long lo = lca, hi = n;
while (lo < hi) {
long mid = (lo + hi + 1) / 2;
long x
= (mid << uBinaryLength) | adjustedUBinary;
long y
= (mid << vBinaryLength) | adjustedVBinary;
// Checking if the combined values
// are within the range
// of valid nodes
if (x <= n && y <= n) {
lo = mid;
}
else {
hi = mid - 1;
}
}
// Printing the result
// (maximum depth)
System.out.println(lo);
}
// Bitwise method to find the LCA of
// two numbers A, B in a Binary Tree
public static long findLCA(long A, long B)
{
while (Long.highestOneBit(B)
> Long.highestOneBit(A))
B /= 2;
while (Long.highestOneBit(A)
> Long.highestOneBit(B))
A /= 2;
while (A != B) {
A /= 2;
B /= 2;
}
return A;
}
}
using System;
class Program
{
// Function to find the Lowest Common Ancestor (LCA) of two
// numbers A and B in a Binary Tree
static long FindLCA(long A, long B)
{
while (B > A)
B >>= 1;
while (A > B)
A >>= 1;
while (A != B)
{
A >>= 1;
B >>= 1;
}
return A;
}
// Method to output the number of pairs
static void CountPairs(long n, long u, long v)
{
// Finding the Lowest Common Ancestor (LCA) of u and v
long lca = FindLCA(u, v);
string lcaBinaryRepresentation = Convert.ToString(lca, 2);
// Getting the binary representations of u and v
string uBinaryRepresentation = Convert.ToString(u, 2);
string vBinaryRepresentation = Convert.ToString(v, 2);
// Adjusting binary representations to align with the
// LCA
int lcaLength = lcaBinaryRepresentation.Length;
uBinaryRepresentation = uBinaryRepresentation.Substring(uBinaryRepresentation.Length - lcaLength);
vBinaryRepresentation = vBinaryRepresentation.Substring(vBinaryRepresentation.Length - lcaLength);
// Converting adjusted binary representations back to
// decimal
long adjustedUBinary = uBinaryRepresentation == "" ? 0 : Convert.ToInt64(uBinaryRepresentation, 2);
long adjustedVBinary = vBinaryRepresentation == "" ? 0 : Convert.ToInt64(vBinaryRepresentation, 2);
// Binary Search algorithm to find the maximum depth
long lo = lca, hi = n;
while (lo < hi)
{
long mid = (lo + hi + 1) / 2;
long x = (mid << lcaLength) | adjustedUBinary;
long y = (mid << lcaLength) | adjustedVBinary;
// Checking if the combined values are within the
// range of valid nodes
if (x <= n && y <= n)
{
lo = mid;
}
else
{
hi = mid - 1;
}
}
// Printing the result (maximum depth)
Console.WriteLine(lo);
}
// Driver Function
static void Main(string[] args)
{
// Inputs
long N = 8;
long A = 1;
long B = 8;
// Function call
CountPairs(N, A, B);
}
}
//This code is contributed by Adarsh.
// Function to find the Lowest Common Ancestor (LCA) of two numbers A, B in a Binary Tree
function findLCA(A, B) {
while (Math.max(B) > Math.max(A)) // Loop until the highest bit of B is greater than the highest bit of A
B >>= 1; // Right shift B by 1 (equivalent to dividing by 2)
while (Math.max(A) > Math.max(B)) // Loop until the highest bit of A is greater than the highest bit of B
A >>= 1; // Right shift A by 1 (equivalent to dividing by 2)
while (A !== B) { // Loop until A is equal to B
A >>= 1; // Right shift A by 1
B >>= 1; // Right shift B by 1
}
return A; // Return the LCA
}
// Method to output the number of pairs
function countPairs(N, u, v) {
// Finding the Lowest Common Ancestor (LCA) of u and v
let lca = findLCA(u, v);
let lcaBinaryRepresentation = lca.toString(2); // Convert LCA to binary representation
// Getting the binary representations of u and v
let uBinaryRepresentation = u.toString(2);
let vBinaryRepresentation = v.toString(2);
// Adjusting binary representations to align with the LCA
uBinaryRepresentation = uBinaryRepresentation.substring(lcaBinaryRepresentation.length);
vBinaryRepresentation = vBinaryRepresentation.substring(lcaBinaryRepresentation.length);
// Converting adjusted binary representations back to decimal
let adjustedUBinary = uBinaryRepresentation.length === 0 ? 0 : parseInt(uBinaryRepresentation, 2);
let adjustedVBinary = vBinaryRepresentation.length === 0 ? 0 : parseInt(vBinaryRepresentation, 2);
// Storing lengths of adjusted binary representations
let uBinaryLength = uBinaryRepresentation.length;
let vBinaryLength = vBinaryRepresentation.length;
// Binary Search algorithm to find the maximum depth
let lo = lca;
let hi = N;
while (lo < hi) {
let mid = Math.floor((lo + hi + 1) / 2);
let x = (mid << uBinaryLength) | adjustedUBinary;
let y = (mid << vBinaryLength) | adjustedVBinary;
// Checking if the combined values are within the range of valid nodes
if (x <= N && y <= N) {
lo = mid;
} else {
hi = mid - 1;
}
}
// Printing the result (maximum depth)
console.log(lo);
}
// Inputs
let N = 8;
let A = 1;
let B = 8;
// Function call
countPairs(N, A, B);
# Function to find the Lowest Common Ancestor (LCA) of two
# numbers A and B in a Binary Tree
def findLCA(A, B):
while B > A:
B >>= 1
while A > B:
A >>= 1
while A != B:
A >>= 1
B >>= 1
return A
# Method to output the number of pairs
def Count_pairs(n, u, v):
# Finding the Lowest Common Ancestor (LCA) of u and v
lca = findLCA(u, v)
lcaBinaryRepresentation = format(lca, '064b')
# Getting the binary representations of u and v
uBinaryRepresentation = format(u, '064b')
vBinaryRepresentation = format(v, '064b')
# Adjusting binary representations to align with the LCA
lcaLength = len(lcaBinaryRepresentation)
uBinaryRepresentation = uBinaryRepresentation[-lcaLength:]
vBinaryRepresentation = vBinaryRepresentation[-lcaLength:]
# Converting adjusted binary representations back to decimal
adjustedUBinary = int(uBinaryRepresentation, 2)
adjustedVBinary = int(vBinaryRepresentation, 2)
# Binary Search algorithm to find the maximum depth
lo, hi = lca, n
while lo < hi:
mid = (lo + hi + 1) // 2
x = (mid << lcaLength) | adjustedUBinary
y = (mid << lcaLength) | adjustedVBinary
# Checking if the combined values are within the range of valid nodes
if x <= n and y <= n:
lo = mid
else:
hi = mid - 1
# Printing the result (maximum depth)
print(lo)
# Driver Function
if __name__ == "__main__":
# Inputs
N = 8
A = 1
B = 8
# Function call
Count_pairs(N, A, B)
#This code is contributed by Utkarsh
Time Complexity: O(logN), As Binary Search is used.
Auxiliary Space: ~O(1)
Comparison of all approaches:
Let’s compare the three approaches in terms of time and space complexity, and other relevant factors:
- First Approach (Stack-Based):
- Time Complexity:
- In Building paths the complexity is: O(log(max(x, y)))
- In Calculating ranges: O(log(n))
- The Overall Time Complexity for first approach is: O(log(max(x, y))) + O(log(n))
- Space Complexity:
- As Stacks for storing paths are used. Therefore, O(log(n)).
- Advantages:
- Explicit path calculations.
- Clarity in binary tree traversal.
- Clearly defined ranges.
- Disadvantages:
- Higher space complexity due to stacks.
- Second Approach (Bit Manipulation):
- Time Complexity:
- In Building paths: O(log(max(x, y)))
- Overall complexity: O(log(max(x, y)))
- Space Complexity:
- Binary representations took O(log(n)) space.
- Advantages:
- Simpler path building.
- No explicit stacks are used, potentially lower space complexity.
- Disadvantages:
- Bit manipulation may be less intuitive for some.
- Third Approach (Binary Search):
- Time Complexity:
- Finding LCA takes O(log(min(A, B))) through Binary Search.
- Space Complexity:
- Binary representations: O(log(n)), which is ~O(1)
- Advantages:
- Efficient use of bitwise operations.
- Binary search reduces time complexity.
- Disadvantages:
- More complex bitwise operations.
- Slightly higher time complexity for finding LCA.
Share your thoughts in the comments
Please Login to comment...