Find ‘N’ number of solutions with the given inequality equations
Last Updated :
21 Aug, 2022
Find the value of a1, a2, a3, ….an such that the following two conditions are satisfied.
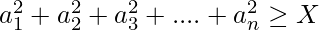
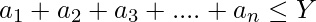
Print the value of a1, a2, …, an and “No solution” otherwise.
Note: There maybe a several solutions, print any of them.
Examples:
Input: n = 5, x = 15, y = 15
Output:
11
1
1
1
1
Input: n = 4, x = 324, y = 77
Output:
74
1
1
1
Approach: Below is the step by step algorithm to solve this problem:
- Initialize the number of elements and the value of x and y.
- There is no solution of a1…a2 if y is less than n or if x is very larger than n.
- Print first solution as y – n + 1 and 1 as the solution of rest of the elements.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define ll long long
void findsolution(ll n, ll x, ll y)
{
if ((y - n + 1) * (y - n + 1) + n - 1 < x || y < n) {
cout << "No solution";
return;
}
cout << y - n + 1;
while (n-- > 1)
cout << endl
<< 1;
}
int main()
{
ll n, x, y;
n = 5, x = 15, y = 15;
findsolution(n, x, y);
return 0;
}
|
Java
import java.io.*;
class GFG {
static void findsolution(long n, long x, long y)
{
if ((y - n + 1) * (y - n + 1) + n - 1 < x || y < n) {
System.out.println( "No solution");
return;
}
System.out.println( y - n + 1);
while (n-- > 1)
System.out.println( "1");
}
public static void main (String[] args) {
long n, x, y;
n = 5; x = 15; y = 15;
findsolution(n, x, y);
}
}
|
Python3
def findsolution(n, x, y):
if ((y - n + 1) * (y - n + 1) +
n - 1 < x or y < n):
print("No solution");
return;
print(y - n + 1);
while (n > 1):
print(1);
n -= 1;
n = 5;
x = 15;
y = 15;
findsolution(n, x, y);
|
C#
using System;
class GFG
{
static void findsolution(long n,
long x, long y)
{
if ((y - n + 1) * (y - n + 1) +
n - 1 < x || y < n)
{
Console.WriteLine( "No solution");
return;
}
Console.WriteLine( y - n + 1);
while (n-- > 1)
Console.WriteLine( "1");
}
static public void Main ()
{
long n, x, y;
n = 5; x = 15; y = 15;
findsolution(n, x, y);
}
}
|
PHP
<?php
function findsolution($n, $x, $y)
{
if (($y - $n + 1) * ($y - $n + 1) +
$n - 1 < $x || $y < $n)
{
echo "No solution";
return;
}
echo $y - $n + 1;
while ($n-- > 1)
echo "\n" . 1;
}
$n = 5; $x = 15; $y = 15;
findsolution($n, $x, $y);
|
Javascript
<script>
function findsolution(n, x, y)
{
if ((y - n + 1) * (y - n + 1) +
n - 1 < x || y < n)
{
document.write( "No solution");
return;
}
document.write( y - n + 1);
while (n-- > 1)
document.write( "<br>" + 1);
}
let n = 5;
let x = 15;
let y = 15;
findsolution(n, x, y);
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...