Find length of longest subsequence of one string which is substring of another string

Given two strings X and Y. The task is to find the length of the longest subsequence of string X which is a substring in sequence Y.

Examples:

Input : X = "ABCD",  Y = "BACDBDCD"
Output : 3
"ACD" is longest subsequence of X which
is substring of Y.

Input : X = "A",  Y = "A"
Output : 1

PREREQUISITES: Longest common subsequence problem will help you understand this problem in a snap 🙂

Method 1 (Brute Force):

Use brute force to find all the subsequences of X and for each subsequence check whether it is a substring of Y or not. If it is a substring of Y, maintain a maximum length variable and compare its length. 

Time Complexity: O(2^n *(n*m)) 

Method 2: (Recursion):

Let n be the length of X and m be the length of Y. We will make a recursive function as follows with 4 arguments and the return type is int as we will get the length of a maximum possible subsequence of X which is the Substring of Y. We will take judgment for further process based on the last char in strings by using n-1 and m-1.

int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
    ....
    return ans;
}

For recursion we need 2 things, we will make 1st the base case and 2nd is calls on smaller input (for that we will see the choice diagram). 

BASE CASE:

By seeing the argument of function we can see only 2 arguments that will change while recursion calls, i.e. lengths of both strings. So for the base case think of the smallest input we can give. You’ll see the smallest input is 0, i.e. empty lengths. hence when n == 0 or m == 0 is the base case. n and m can’t be less than zero. Now we know the condition and we need to return the length of subsequence as per the question. if the length is 0, then means one of the string is empty, and there is no common subsequence possible, so we have to return 0 for the same.

int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
    if (n==0 || m==0) return 0;
    ....
    return ans;
}

CHILDREN CALLS: 

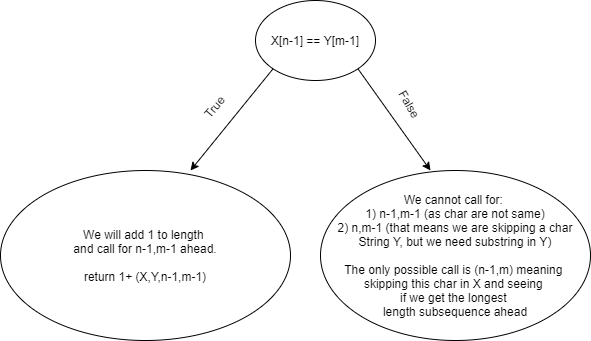
Choice Diagram

We can see how to make calls by seeing if the last char of both strings are the same or not. We can see how this is slightly different from the LCS (Longest Common Subsequence) question.

int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
    // Base Case
    if (n==0 || m==0) return 0;
    
    // Calls on smaller inputs
    
    // if the last char of both strings are equal
    if(X[n-1] == Y[m-1])
    {
        return  1 + maxSubsequenceSubstring(X,Y,n-1,m-1);
    }
    
    // if the last char of both strings are not equal
    else
    {
        return maxSubsequenceSubstring(X,Y,n-1,m);    
    }
}

Now here is the main crux of the question, we can see we are calling for X[0..n] and Y[0..m], in our recursion function it will return the answer of maximum length of the subsequence of X, and Substring of Y (and the ending char of that substring of Y ends at length m). This is very important as we want to find all intermediary substrings also. hence we need to use a for loop where we will call the above function for all the lengths from 0 to m of Y, and return the maximum of the answer there. Here is the final code in C++ for the same.

Implementation:

C++

#include<bits/stdc++.h>
using namespace std;

int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
    // Base Case
    if (n==0 || m==0) return 0;

    // Calls on smaller inputs

    // if the last char of both strings are equal
    if(X[n-1] == Y[m-1])
    {
        return  1 + maxSubsequenceSubstring(X,Y,n-1,m-1);
    }

    // if the last char of both strings are not equal
    else
    {
        return maxSubsequenceSubstring(X,Y,n-1,m);
    }
}

int main()
{
     string X = "abcd";
      string Y = "bacdbdcd";
      int n = X.size(),m = Y.size();
      int maximum_length = 0; //as minimum length can be 0 only.
      for(int i = 0;i<=m;i++) // traversing for every length of Y.
    {
        int temp_ans = maxSubsequenceSubstring(X,Y,n,i);
          if(temp_ans > maximum_length) maximum_length = temp_ans;
    }
      cout<<"Length for maximum possible Subsequence of string X which is Substring of Y -> "<<maximum_length;
      return 0;
}

Java

import java.util.*;
class GFG {

    static int maxSubsequenceSubString(String X, String Y,
                                       int n, int m)
    {

        // Base Case
        if (n == 0 || m == 0)
            return 0;

        // Calls on smaller inputs

        // if the last char of both Strings are equal
        if (X.charAt(n - 1) == Y.charAt(m - 1)) {
            return 1
                + maxSubsequenceSubString(X, Y, n - 1,
                                          m - 1);
        }

        // if the last char of both Strings are not equal
        else {
            return maxSubsequenceSubString(X, Y, n - 1, m);
        }
    }

  // Driver code
    public static void main(String[] args)
    {
        String X = "abcd";
        String Y = "bacdbdcd";
        int n = X.length(), m = Y.length();
        int maximum_length
            = 0; // as minimum length can be 0 only.
        for (int i = 0; i <= m;
             i++) // traversing for every length of Y.
        {
            int temp_ans
                = maxSubsequenceSubString(X, Y, n, i);
            if (temp_ans > maximum_length)
                maximum_length = temp_ans;
        }
        System.out.print(
            "Length for maximum possible Subsequence of String X which is SubString of Y->"
            + maximum_length);
    }
}

// This code is contributed by gauravrajput1

Python3

def maxSubsequenceSubstring(X, Y, n, m):

    # Base Case
    if (n == 0 or m == 0):
        return 0

    # Calls on smaller inputs

    # if the last char of both strings are equal
    if(X[n - 1] == Y[m - 1]):
        return 1 + maxSubsequenceSubstring(X, Y, n - 1, m - 1)

    # if the last char of both strings are not equal
    else:
        return maxSubsequenceSubstring(X, Y, n - 1, m)

# driver code
X = "abcd"
Y = "bacdbdcd"
n, m = len(X), len(Y)
maximum_length = 0 #as minimum length can be 0 only.
for i in range(m + 1):# traversing for every length of Y.

    temp_ans = maxSubsequenceSubstring(X, Y, n, i)
    if(temp_ans > maximum_length):
         maximum_length = temp_ans

print(f"Length for maximum possible Subsequence of string X which is Substring of Y -> {maximum_length}")

# This code is contributed by shinjanpatra

C#

using System;

public class GFG {

    static int maxSubsequenceSubString(String X, String Y,
                                       int n, int m)
    {

        // Base Case
        if (n == 0 || m == 0)
            return 0;

        // Calls on smaller inputs

        // if the last char of both Strings are equal
        if (X[n - 1] == Y[m - 1]) {
            return 1
                + maxSubsequenceSubString(X, Y, n - 1,
                                          m - 1);
        }

        // if the last char of both Strings are not equal
        else {
            return maxSubsequenceSubString(X, Y, n - 1, m);
        }
    }

    // Driver code
    public static void Main(String[] args)
    {
        String X = "abcd";
        String Y = "bacdbdcd";
        int n = X.Length, m = Y.Length;
        int maximum_length
            = 0; // as minimum length can be 0 only.
        for (int i = 0; i <= m;
             i++) // traversing for every length of Y.
        {
            int temp_ans
                = maxSubsequenceSubString(X, Y, n, i);
            if (temp_ans > maximum_length)
                maximum_length = temp_ans;
        }
        Console.Write(
            "Length for maximum possible Subsequence of String X which is SubString of Y->"
            + maximum_length);
    }
}

// This code is contributed by gauravrajput1

Javascript

<script>

function maxSubsequenceSubstring(X,Y,n,m)
{
    // Base Case
    if (n==0 || m==0) return 0;

    // Calls on smaller inputs

    // if the last char of both strings are equal
    if(X[n-1] == Y[m-1])
    {
        return 1 + maxSubsequenceSubstring(X,Y,n-1,m-1);
    }

    // if the last char of both strings are not equal
    else
    {
        return maxSubsequenceSubstring(X,Y,n-1,m);
    }
}

// driver code

let X = "abcd";
let Y = "bacdbdcd";
let n = X.length,m = Y.length;
let maximum_length = 0; //as minimum length can be 0 only.
for(let i = 0;i<=m;i++) // traversing for every length of Y.
{
    let temp_ans = maxSubsequenceSubstring(X,Y,n,i);
    if(temp_ans > maximum_length) maximum_length = temp_ans;
}
document.write("Length for maximum possible Subsequence of string X which is Substring of Y -> "+ maximum_length);

// This code is contributed by shinjanpatra

</script>

Output

Length for maximum possible Subsequence of string X which is Substring of Y -> 3

Time Complexity: O(n*m) (For every call in the recursion function we are decreasing n, hence we will reach the base case exactly after n calls, and we are using for loop for m times for the different lengths of string Y).

Space Complexity: O(n) (For recursion calls we are using stacks for each call).

Method 3: (Dynamic Programming):

Submethod 1:-  Memoization

NOTE: Must see the above recursion solution to understand its optimization as Memoization

From the above recursion solution, there are multiple calls and further, we are using recursion in for loop, there is a high probability we have already solved the answer for a call. hence to optimize our recursion solution we will use? (See we have only 2 arguments that vary throughout the calls, hence the dimension of the array is 2 and the size is 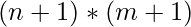 because we need to store answers for all possible calls from 0..n and 0..m). Hence it is a 2D array.

we can use vectors for the same or dynamic allocation of the array.

// initialise a vector like this
vector<vector<int>> dp(n+1,vector<int>(m+1,-1));

// or Dynamic allocation
int **dp = new int*[n+1];
for(int i = 0;i<=n;i++)
{
    dp[i] = new int[m+1];
    for(int j = 0;j<=m;j++)
    {
        dp[i][j] = -1;
    }
}

By initializing the 2D vector we will use this array as the 5th argument in recursion and store our answer. also, we have filled it with -1, which means we have not solved this call hence use traditional recursion for it, if dp[n][m] at any call is not -1, means we have already solved the call, hence use the answer of dp[n][m].

// In recursion calls we will check for if we have solved the answer for the call or not
if(dp[n][m] != -1) return dp[n][m];

// Else we will store the result and return that back from this call
if(X[n-1] == Y[m-1]) 
    return dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
else 
    return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);

Code for memoization is here:

C++

#include<bits/stdc++.h>
using namespace std;

int maxSubsequenceSubstring(string &X,string &Y,int n,int m,vector<vector<int>>& dp)
{
    // Base Case
    if (n==0 || m==0) return 0;

      // check if we have already solved it?
      if(dp[n][m] != -1) return dp[n][m];


    // Calls on smaller inputs

    // if the last char of both strings are equal
    if(X[n-1] == Y[m-1])
    {
        return  dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
    }

    // if the last char of both strings are not equal
    else
    {
        return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);
    }
}

int main()
{
     string X = "abcd";
      string Y = "bacdbdcd";
      int n = X.size(),m = Y.size();
      int maximum_length = 0; //as minimum length can be 0 only.

      vector<vector<int>> dp(n+1,vector<int>(m+1,-1));
      for(int i = 0;i<=m;i++) // traversing for every length of Y.
    {
        int temp_ans = maxSubsequenceSubstring(X,Y,n,i,dp);
          if(temp_ans > maximum_length) maximum_length = temp_ans;
    }
      cout<<"Length for maximum possible Subsequence of string X which is Substring of Y -> "<<maximum_length;
      return 0;
}

Java

/*package whatever //do not write package name here */

import java.io.*;
import java.util.*;

class GFG {
    static int maxSubsequenceSubstring(String X,String Y,int n,int m,int dp[][])
    {
        // Base Case
        if (n==0 || m==0) return 0;

        // check if we have already solved it?
        if(dp[n][m] != -1) return dp[n][m];


        // Calls on smaller inputs

        // if the last char of both strings are equal
        if(X.charAt(n-1) == Y.charAt(m-1))
        {
            return dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
        }

        // if the last char of both strings are not equal
        else
        {
            return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);
        }
    }

// Driver Code
public static void main(String args[])
{
    String X = "abcd";
    String Y = "bacdbdcd";
    int n = X.length(),m = Y.length();
    int maximum_length = 0; //as minimum length can be 0 only.

    int dp[][] = new int[n+1][m+1];
    for(int i = 0; i < n + 1; i++){
        Arrays.fill(dp[i], -1);
    }
    for(int i = 0;i<=m;i++) // traversing for every length of Y.
    {
        int temp_ans = maxSubsequenceSubstring(X,Y,n,i,dp);
        if(temp_ans > maximum_length) maximum_length = temp_ans;
    }
    System.out.println("Length for maximum possible Subsequence of string X which is Substring of Y -> "+maximum_length);
}
}

// This code is contributed by shinjanpatra

Python3

# Python implementation of above approach
def maxSubsequenceSubstring(X, Y, n, m, dp):

    # Base Case
    if (n == 0 or m == 0):
        return 0

    # check if we have already solved it?
    if(dp[n][m] != -1):
        return dp[n][m]

    # Calls on smaller inputs

    # if the last char of both strings are equal
    if(X[n - 1] == Y[m - 1]):
        dp[n][m] = 1 + maxSubsequenceSubstring(X, Y, n - 1, m - 1, dp)
        return dp[n][m]

    # if the last char of both strings are not equal
    else:
        dp[n][m] = maxSubsequenceSubstring(X, Y, n - 1, m, dp)
        return dp[n][m]

# driver code
X = "abcd"
Y = "bacdbdcd"
n,m = len(X),len(Y)
maximum_length = 0 #as minimum length can be 0 only.

dp = [[-1 for i in range(m+1)]for j in range(n+1)]

for i in range(m+1): # traversing for every length of Y.

    temp_ans = maxSubsequenceSubstring(X, Y, n, i, dp)
    if(temp_ans > maximum_length):
        maximum_length = temp_ans

print("Length for maximum possible Subsequence of string X which is Substring of Y -> "+str(maximum_length))

# This code is contributed by shinjanpatra

C#

// C# code for the above approach
using System;

class GFG
{
  static int maxSubsequenceSubstring(string X, string Y, int n, int m, int[,] dp)
  {
    // Base Case
    if (n == 0 || m == 0) return 0;

    // check if we have already solved it?
    if (dp[n, m] != -1) return dp[n, m];

    // Calls on smaller inputs

    // if the last char of both strings are equal
    if (X[n - 1] == Y[m - 1])
    {
      return dp[n, m] = 1 + maxSubsequenceSubstring(X, Y, n - 1, m - 1, dp);
    }

    // if the last char of both strings are not equal
    else
    {
      return dp[n, m] = maxSubsequenceSubstring(X, Y, n - 1, m, dp);
    }
  }

  // Driver Code
  public static void Main(string[] args)
  {
    string X = "abcd";
    string Y = "bacdbdcd";
    int n = X.Length, m = Y.Length;
    int maximum_length = 0; //as minimum length can be 0 only.

    int[,] dp = new int[n + 1, m + 1];
    for (int i = 0; i < n + 1; i++)
    {
      for (int j = 0; j < m + 1; j++)
      {
        dp[i, j] = -1;
      }
    }
    for (int i = 0; i <= m; i++) // traversing for every length of Y.
    {
      int temp_ans = maxSubsequenceSubstring(X, Y, n, i, dp);
      if (temp_ans > maximum_length) maximum_length = temp_ans;
    }
    Console.WriteLine("Length for maximum possible Subsequence of string X which is Substring of Y -> " + maximum_length);
  }
}

// This code is contributed by lokeshpotta20.

Javascript

<script>

// JavaScript implementation of above approach


function maxSubsequenceSubstring(X,Y,n,m,dp)
{
    // Base Case
    if (n==0 || m==0) return 0;

      // check if we have already solved it?
      if(dp[n][m] != -1) return dp[n][m];


    // Calls on smaller inputs

    // if the last char of both strings are equal
    if(X[n-1] == Y[m-1])
    {
        return  dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
    }

    // if the last char of both strings are not equal
    else
    {
        return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);
    }
}

// driver code

let X = "abcd";
let Y = "bacdbdcd";
let n = X.length,m = Y.length;
let maximum_length = 0; //as minimum length can be 0 only.

let dp = new Array(n+1);
for(let i=0;i<n+1;i++){
    dp[i] = new Array(m+1).fill(-1);
}
for(let i = 0;i<=m;i++) // traversing for every length of Y.
{
    let temp_ans = maxSubsequenceSubstring(X,Y,n,i,dp);
    if(temp_ans > maximum_length) maximum_length = temp_ans;
}
document.write("Length for maximum possible Subsequence of string X which is Substring of Y -> ",maximum_length);

// This code is contributed by shinjanpatra

</script>

Output

Length for maximum possible Subsequence of string X which is Substring of Y -> 3

Time Complexity: O(n*m) (It will be definitely better than the recursion solution, the worst case is possible only possible when none of the char of string X is there in String Y.)
Space Complexity: O(n*m + n) (the Size of Dp array and stack call size of recursion)

Submethod 2:  Tabulation

Let n be length of X and m be length of Y. Create a 2D array ‘dp[][]’ of m + 1 rows and n + 1 columns. Value dp[i][j] is maximum length of subsequence of X[0….j] which is substring of Y[0….i]. Now for each cell of dp[][] fill value as : 

for (i = 1 to m)
  for (j = 1 to n)
    if (x[j-1] == y[i - 1])
      dp[i][j] = dp[i-1][j-1] + 1;
    else
      dp[i][j] = dp[i][j-1];

And finally, the length of the longest subsequence of x which is substring of y is max(dp[i][n]) where 1 <= i <= m.

Below is implementing this approach:

C++

// C++ code to implement the approach
#include <bits/stdc++.h>
using namespace std;

const int MAX = 1000;

// Return the maximum size of substring of
// X which is substring in Y.
int maxSubsequenceSubstring(string x,string y,int n,int m)
{
    vector<vector<int>>dp(MAX,vector<int>(MAX,0));

    // Calculating value for each element.
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {

            // If alphabet of string X and Y are
            // equal make dp[i][j] = 1 + dp[i-1][j-1]
            if (x[j - 1] == y[i - 1])
                dp[i][j] = 1 + dp[i - 1][j - 1];

            // Else copy the previous value in the
            // row i.e dp[i-1][j-1]
            else
                dp[i][j] = dp[i][j - 1];
        }
    }

    // Finding the maximum length.
    int ans = 0;
    for (int i = 1; i <= m; i++)
        ans = max(ans, dp[i][n]);

    return ans;
}

// Driver code
int main()
{
    string x = "ABCD";
    string y = "BACDBDCD";
    int n = x.length(), m = y.length();
    cout<<maxSubsequenceSubstring(x, y, n, m);
}

// This code is contributed by shinjanpatra

Java

// Java program to find maximum length of
// subsequence of a string X such it is
// substring in another string Y.

public class GFG
{
    static final int MAX = 1000;

    // Return the maximum size of substring of
    // X which is substring in Y.
    static int maxSubsequenceSubstring(char x[], char y[],
                                int n, int m)
    {
        int dp[][] = new int[MAX][MAX];

        // Initialize the dp[][] to 0.
        for (int i = 0; i <= m; i++)
            for (int j = 0; j <= n; j++)
                dp[i][j] = 0;

        // Calculating value for each element.
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {

                // If alphabet of string X and Y are
                // equal make dp[i][j] = 1 + dp[i-1][j-1]
                if (x[j - 1] == y[i - 1])
                    dp[i][j] = 1 + dp[i - 1][j - 1];

                // Else copy the previous value in the
                // row i.e dp[i-1][j-1]
                else
                    dp[i][j] = dp[i][j - 1];
            }
        }

        // Finding the maximum length.
        int ans = 0;
        for (int i = 1; i <= m; i++)
            ans = Math.max(ans, dp[i][n]);

        return ans;
    }

    // Driver Method
    public static void main(String[] args)
    {
        char x[] = "ABCD".toCharArray();
        char y[] = "BACDBDCD".toCharArray();
        int n = x.length, m = y.length;
        System.out.println(maxSubsequenceSubstring(x, y, n, m));
    }
}

Python3

# Python3 program to find maximum
# length of subsequence of a string
# X such it is substring in another
# string Y.

MAX = 1000

# Return the maximum size of
# substring of X which is
# substring in Y.
def maxSubsequenceSubstring(x, y, n, m):
    dp = [[0 for i in range(MAX)]
             for i in range(MAX)]

    # Initialize the dp[][] to 0.

    # Calculating value for each element.
    for i in range(1, m + 1):
        for j in range(1, n + 1):

            # If alphabet of string
            # X and Y are equal make
            # dp[i][j] = 1 + dp[i-1][j-1]
            if(x[j - 1] == y[i - 1]):
                dp[i][j] = 1 + dp[i - 1][j - 1]

            # Else copy the previous value
            # in the row i.e dp[i-1][j-1]
            else:
                dp[i][j] = dp[i][j - 1]

    # Finding the maximum length
    ans = 0
    for i in range(1, m + 1):
        ans = max(ans, dp[i][n])
    return ans

# Driver Code
x = "ABCD"
y = "BACDBDCD"
n = len(x)
m = len(y)
print(maxSubsequenceSubstring(x, y, n, m))

# This code is contributed
# by sahilshelangia

C#

// C# program to find maximum length of
// subsequence of a string X such it is
// substring in another string Y.
using System;

public class GFG
{
    static int MAX = 1000;

    // Return the maximum size of substring of
    // X which is substring in Y.
    static int maxSubsequenceSubstring(string x, string y,
                                            int n, int m)
    {
        int[ ,]dp = new int[MAX, MAX];

        // Initialize the dp[][] to 0.
        for (int i = 0; i <= m; i++)
            for (int j = 0; j <= n; j++)
                dp[i, j] = 0;

        // Calculating value for each element.
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {

                // If alphabet of string X and Y are
                // equal make dp[i][j] = 1 + dp[i-1][j-1]
                if (x[j - 1] == y[i - 1])
                    dp[i, j] = 1 + dp[i - 1, j - 1];

                // Else copy the previous value in the
                // row i.e dp[i-1][j-1]
                else
                    dp[i, j] = dp[i, j - 1];
            }
        }

        // Finding the maximum length.
        int ans = 0;

        for (int i = 1; i <= m; i++)
            ans = Math.Max(ans, dp[i,n]);

        return ans;
    }

    // Driver Method
    public static void Main()
    {
        string x = "ABCD";
        string y = "BACDBDCD";
        int n = x.Length, m = y.Length;

        Console.WriteLine(maxSubsequenceSubstring(x,
                                            y, n, m));
    }
}

// This code is contributed by vt_m.

PHP

<?php
// PHP program to find maximum length of
// subsequence of a string X such it is
// substring in another string Y.

// Return the maximum size of substring of
// X which is substring in Y.
function maxSubsequenceSubstring($x, $y,
                                 $n, $m)
{
    $dp;

    // Initialize the dp[][] to 0.
    for ($i = 0; $i <= $m; $i++)
        for ($j = 0; $j <= $n; $j++)
            $dp[$i][$j] = 0;

    // Calculating value for each element.
    for ($i = 1; $i <= $m; $i++) {
        for ( $j = 1; $j <= $n; $j++) {

            // If alphabet of string
            // X and Y are equal make
            // dp[i][j] = 1 + dp[i-1][j-1]
            if ($x[$j - 1] == $y[$i - 1])
                $dp[$i][$j] = 1 + $dp[$i - 1][$j - 1];

            // Else copy the previous
            // value in the
            // row i.e dp[i-1][j-1]
            else
                $dp[$i][$j] = $dp[$i][$j - 1];
        }
    }

    // Finding the maximum length.
    $ans = 0;
    for ( $i = 1; $i <= $m; $i++)
        $ans = max($ans, $dp[$i][$n]);

    return $ans;
}

// Driver Code
{
    $x = "ABCD";
    $y = "BACDBDCD";
    $n = strlen($x); $m = strlen($y);
    echo maxSubsequenceSubstring($x, $y, $n, $m);
    return 0;
}

// This code is contributed by nitin mittal
?>

Javascript

<script>


// Javascript program to find maximum length of
// subsequence of a string X such it is
// substring in another string Y.
var MAX = 1000;

// Return the maximum size of substring of
// X which is substring in Y.
function maxSubsequenceSubstring(x, y, n, m)
{
    var dp = Array.from(Array(MAX), ()=> Array(MAX));

    // Initialize the dp[][] to 0.
    for (var i = 0; i <= m; i++)
        for (var j = 0; j <= n; j++)
            dp[i][j] = 0;

    // Calculating value for each element.
    for (var i = 1; i <= m; i++) {
        for (var j = 1; j <= n; j++) {

            // If alphabet of string X and Y are
            // equal make dp[i][j] = 1 + dp[i-1][j-1]
            if (x[j - 1] == y[i - 1])
                dp[i][j] = 1 + dp[i - 1][j - 1];

            // Else copy the previous value in the
            // row i.e dp[i-1][j-1]
            else
                dp[i][j] = dp[i][j - 1];
        }
    }

    // Finding the maximum length.
    var ans = 0;
    for (var i = 1; i <= m; i++)
        ans = Math.max(ans, dp[i][n]);

    return ans;
}

// Driver Program
var x = "ABCD";
var y = "BACDBDCD";
var n = x.length, m = y.length;
document.write( maxSubsequenceSubstring(x, y, n, m));

</script>

Output

3

Time Complexity: O(n*m) (Time required to fill the Dp array)
Space Complexity: O(n*m + n) (the Size of Dp array)

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.