Factorial of Large numbers using Logarithmic identity

Given a very large number N, the task is to find the factorial of the number using Log.

Factorial of a non-negative integer is the multiplication of all integers smaller than or equal to N.

We have previously discussed a simple program to find the factorial in this article. Here, we will discuss an efficient way to find the factorial of large numbers. Examples:

Input: N = 100 Output: 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000 Input: N = 50 Output: 30414093201713378043612608166064768844377641568960512000000000000

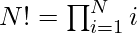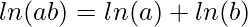Approach: The most common iterative version runs in expected O(N) time. But as numbers become big it will be wrong to assume that multiplication takes constant time. The naive approach takes O(K*M) time for multiplication where K is the length of the multiplier and M is the length of the multiplicand. Therefore, the idea is to use logarithmic properties: As we know that and Therefore: 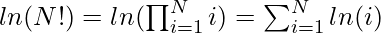Another property is 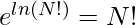by substituting the value of ln(N!). Below is the implementation of the above approach: 

C++

// C++ program to compute the
// factorial of big numbers

#include <bits/stdc++.h>
using namespace std;

// Maximum number of digits
// in output
#define MAX 1000

// Function to find the factorial
// of large number and return
// them in string format
string factorial(long long n)
{
    if (n > MAX) {
        cout << " Integer Overflow"
             << endl;
        return "";
    }

    long long counter;
    long double sum = 0;

    // Base case
    if (n == 0)
        return "1";

    // Calculate the sum of
    // logarithmic values

    for (counter = 1; counter <= n;
         counter++) {
        sum = sum + log(counter);
    }

    // Number becomes too big to hold in
    // unsigned long integers.
    // Hence converted to string
    // Answer is sometimes under
    // estimated due to floating point
    // operations so round() is used
    string result
        = to_string(round(exp(sum)));

    return result;
}

// Driver code
int main()
{
    clock_t tStart = clock();
    string str;
    str = factorial(100);
    cout << "The factorial is: "
         << str << endl;

    // Calculates the time taken
    // by the algorithm to execute
    cout << "Time taken: " << setprecision(10)
         << ((double)(clock() - tStart)
             / CLOCKS_PER_SEC)
         << " s" << endl;
}

Python3

# Python program to compute the
# factorial of big numbers
import math
import time

# Maximum number of digits
# in output
MAX=1000

# Function to find the factorial
# of large number and return
# them in string format
def factorial(n):
    if(n > MAX):
        print(" Integer Overflow")
        return ""

    counter = 0
    sum = 0

    # Base case
    if(n == 0):
        return "1"

    # Calculate the sum of
    # logarithmic values

    for counter in range(1,n+1):
        sum = sum + math.log(counter)

    # Number becomes too big to hold in
    # unsigned long integers.
    # Hence converted to string
    # Answer is sometimes under
    # estimated due to floating point
    # operations so round() is used
    result = str(round(math.exp(sum)))

    return result

# Driver code
tStart = time.perf_counter()
str = factorial(100)
print("The factorial is: ",end="")
print(str)

# Calculates the time taken
# by the algorithm to execute
tEnd = time.perf_counter()
print("Time taken: ",end="")
print('%.10f' % (tEnd-tStart),end="")
print(" s")

# This code is contributed by Pushpesh Raj.

Output:The factorial is: 93326215443944231979346762015249956831505959550546075483971433508015162170687116519232751238036777284091181469944786448222582618323317549251483571058789842944.000000 Time taken: 0.000114 s

Time Complexity: O(N), where N is the given number.

Space complexity: O(1) since using constant variables