Factorial of Large numbers using Logarithmic identity
Last Updated :
07 Jan, 2024
Given a very large number N, the task is to find the factorial of the number using Log.
Factorial of a non-negative integer is the multiplication of all integers smaller than or equal to N.
We have previously discussed a simple program to find the factorial in this article. Here, we will discuss an efficient way to find the factorial of large numbers. Examples:
Input: N = 100
Output: 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
Input: N = 50
Output: 30414093201713378043612608166064768844377641568960512000000000000
Approach: The most common iterative version runs in expected O(N) time. But as numbers become big it will be wrong to assume that multiplication takes constant time. The naive approach takes O(K*M) time for multiplication where K is the length of the multiplier and M is the length of the multiplicand. Therefore, the idea is to use logarithmic properties: As we know that 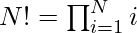 and
and 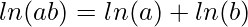 Therefore:
Therefore: 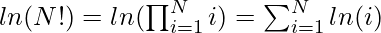 Another property is
Another property is 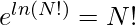 by substituting the value of ln(N!). Below is the implementation of the above approach:
by substituting the value of ln(N!). Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define MAX 1000
string factorial(long long n)
{
if (n > MAX) {
cout << " Integer Overflow"
<< endl;
return "";
}
long long counter;
long double sum = 0;
if (n == 0)
return "1";
for (counter = 1; counter <= n;
counter++) {
sum = sum + log(counter);
}
string result
= to_string(round(exp(sum)));
return result;
}
int main()
{
clock_t tStart = clock();
string str;
str = factorial(100);
cout << "The factorial is: "
<< str << endl;
cout << "Time taken: " << setprecision(10)
<< ((double)(clock() - tStart)
/ CLOCKS_PER_SEC)
<< " s" << endl;
}
|
Java
import java.math.BigDecimal;
import java.math.RoundingMode;
public class Factorial {
static int MAX = 1000;
static String factorial(int n) {
if (n > MAX) {
System.out.println(" Integer Overflow");
return "";
}
int counter;
double sum = 0;
if (n == 0)
return "1";
for (counter = 1; counter <= n; counter++) {
sum = sum + Math.log(counter);
}
BigDecimal result = new BigDecimal(Math.exp(sum));
result = result.setScale(0, RoundingMode.HALF_UP);
return result.toString();
}
public static void main(String[] args) {
long startTime = System.currentTimeMillis();
String str;
str = factorial(100);
System.out.println("The factorial is: " + str);
System.out.println("Time taken: " + (System.currentTimeMillis() - startTime) + " ms");
}
}
|
Python3
import math
import time
MAX=1000
def factorial(n):
if(n > MAX):
print(" Integer Overflow")
return ""
counter = 0
sum = 0
if(n == 0):
return "1"
for counter in range(1,n+1):
sum = sum + math.log(counter)
result = str(round(math.exp(sum)))
return result
tStart = time.perf_counter()
str = factorial(100)
print("The factorial is: ",end="")
print(str)
tEnd = time.perf_counter()
print("Time taken: ",end="")
print('%.10f' % (tEnd-tStart),end="")
print(" s")
|
Javascript
function factorial(n) {
const MAX = 1000;
if (n > MAX) {
console.log(" Integer Overflow");
return "";
}
let counter;
let sum = 0;
if (n === 0)
return "1";
for (counter = 1; counter <= n; counter++) {
sum = sum + Math.log(counter);
}
const result = BigInt(Math.round(Math.exp(sum))).toString();
return result;
}
const startTime = Date.now();
let str;
str = factorial(100);
console.log("The factorial is: " + str);
console.log("Time taken: " + (Date.now() - startTime) + " ms");
|
C#
using System;
using System.Diagnostics;
using System.Numerics;
public class Factorial {
const int MAX = 1000;
static string ComputeFactorial(long n) {
if (n > MAX) {
Console.WriteLine(" Integer Overflow");
return "";
}
long counter;
double sum = 0;
if (n == 0)
return "1";
for (counter = 1; counter <= n; counter++) {
sum = sum + Math.Log(counter);
}
string result = BigInteger.Exp(sum).ToString();
return result;
}
static void Main(string[] args) {
Stopwatch stopwatch = Stopwatch.StartNew();
string str;
str = ComputeFactorial(100);
Console.WriteLine("The factorial is: " + str);
Console.WriteLine("Time taken: " + stopwatch.Elapsed.TotalSeconds.ToString("0.000000") + " s");
}
}
|
OutputThe factorial is: 93326215443944231979346762015249956831505959550546075483971433508015162170687116519232751238036777284091181469944786448222582618323317549251483571058789842944.000000
Time taken: 0.000198 s
Time Complexity: O(N), where N is the given number.
Auxiliary Space: O(1) since using constant variables
Share your thoughts in the comments
Please Login to comment...