Expected number of coin flips to get two heads in a row?
Last Updated :
07 Dec, 2018
Problem : Find the expected number of times a coin must be flipped to get two heads consecutively?
Solution : The key is to observe that if we see a tail on the first flip, it basically ruins any streak and so we have to start over again. In other words, the first tails makes all the previous tosses “wasted” and that increases the conditional expected time by that many tosses.
Let the expected number of coin flips be
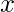
. Now, there are three possible cases as listed below:
- If a tail appears on the first flip of coin. If in the first flip, a tail occurs then it means that we have wasted one flip and we will have to do
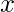 more flips to reach our goal. The probability of this event is 1/2 and the total number of flips now required will be x+1.
more flips to reach our goal. The probability of this event is 1/2 and the total number of flips now required will be x+1.
- If a heads appears on the first flip of coin and a tails appears on the second flip. In this case it means that we have wasted two flips and we will have to do
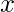 more flips to reach our goal. Therefore the total number of flips now required will be x+2 and the probability of this event is 1/4.
more flips to reach our goal. Therefore the total number of flips now required will be x+2 and the probability of this event is 1/4.
- The last case is, if we get two consecutive heads on two consecutive flips of the coin respectively. The probability of this event is 1/4 and the total number of flips required will be 2.
Framing the above three cases in the form of equations and adding we will get:
x = (1/2)(x+1) + (1/4)(x+2) + (1/4)2
x = 1/2 [ (1+x) + 1/2(2+x) + 1 ]
x = 1/2 [ 1 + x + 1 + x/2 + 1 ]
x / 4 = 3/2
x = 6
Therefore,
x = 6.
Thus, the expected number of coin flips for getting two consecutive heads is 6.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...