Estimating the value of Pi using Monte Carlo

Monte Carlo estimation
Monte Carlo methods are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. One of the basic examples of getting started with the Monte Carlo algorithm is the estimation of Pi. 
Estimation of Pi
The idea is to simulate random (x, y) points in a 2-D plane with domain as a square of side 2r units centered on (0,0). Imagine a circle inside the same domain with same radius r and inscribed into the square. We then calculate the ratio of number points that lied inside the circle and total number of generated points. Refer to the image below:

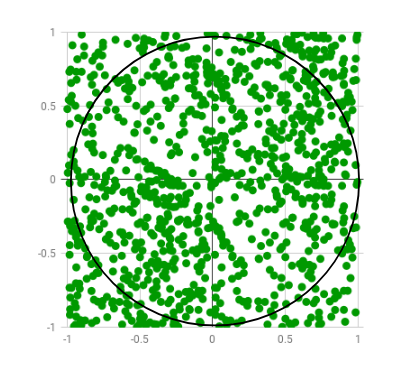
Random points are generated only few of which lie outside the imaginary circle

We know that area of the square is 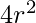 unit sq while that of circle is 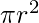.  The ratio of these two areas is as follows :

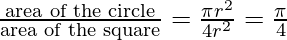
Now for a very large number of generated points, 

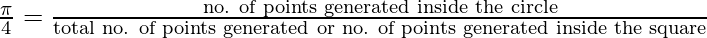that is,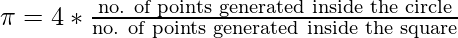

The beauty of this algorithm is that we don’t need any graphics or simulation to display the generated points. We simply generate random (x, y) pairs and then check if 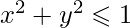. If yes, we increment the number of points that appears inside the circle. In randomized and simulation algorithms like Monte Carlo, the more the number of iterations, the more accurate the result is. Thus, the title is “Estimating the value of Pi” and not “Calculating the value of Pi”. Below is the algorithm for the method:
The Algorithm
1. Initialize circle_points, square_points and interval to 0. 
2. Generate random point x. 
3. Generate random point y. 
4. Calculate d = x*x + y*y. 
5. If d <= 1, increment circle_points. 
6. Increment square_points. 
7. Increment interval. 
8. If increment < NO_OF_ITERATIONS, repeat from 2. 
9. Calculate pi = 4*(circle_points/square_points). 
10. Terminate.
The code doesn’t wait for any input via stdin as the macro INTERVAL could be changed as per the required number of iterations. Number of iterations are the square of INTERVAL. Also, I’ve paused the screen for first 10 iterations with getch() and outputs are displayed for every iteration with format given below. You can change or delete them as per requirement. 

x y circle_points square_points - pi 

Examples:

INTERVAL = 5
Output : Final Estimation of Pi = 2.56

INTERVAL = 10
Output : Final Estimation of Pi = 3.24

INTERVAL = 100
Output : Final Estimation of Pi = 3.0916

C++

/* C++ program for estimation of Pi using Monte
   Carlo Simulation */
#include <bits/stdc++.h>

// Defines precision for x and y values. More the
// interval, more the number of significant digits
#define INTERVAL 10000
using namespace std;

int main()
{
    int interval, i;
    double rand_x, rand_y, origin_dist, pi;
    int circle_points = 0, square_points = 0;

    // Initializing rand()
    srand(time(NULL));

    // Total Random numbers generated = possible x
    // values * possible y values
    for (i = 0; i < (INTERVAL * INTERVAL); i++) {

        // Randomly generated x and y values
        rand_x = double(rand() % (INTERVAL + 1)) / INTERVAL;
        rand_y = double(rand() % (INTERVAL + 1)) / INTERVAL;

        // Distance between (x, y) from the origin
        origin_dist = rand_x * rand_x + rand_y * rand_y;

        // Checking if (x, y) lies inside the define
        // circle with R=1
        if (origin_dist <= 1)
            circle_points++;

        // Total number of points generated
        square_points++;

        // estimated pi after this iteration
        pi = double(4 * circle_points) / square_points;

        // For visual understanding (Optional)
        cout << rand_x << " " << rand_y << " "
             << circle_points << " " << square_points
             << " - " << pi << endl
             << endl;

        // Pausing estimation for first 10 values (Optional)
        if (i < 20)
            getchar();
    }

    // Final Estimated Value
    cout << "\nFinal Estimation of Pi = " << pi;

    return 0;
}

Java

// Java program for estimation of Pi using Monte
//Carlo Simulation
import java.util.*;
import java.io.*;
import java.util.concurrent.ThreadLocalRandom;

class GFG
{
    // Defines precision for x and y values. More the
    // interval, more the number of significant digits
    static int INTERVAL = 10000;

    // Driver code
    public static void main(String[] args)throws IOException
    {
        double rand_x, rand_y, origin_dist, pi=0;
        int circle_points = 0, square_points = 0;

        // Total Random numbers generated = possible x
        // values * possible y values
        for (int i = 0; i < (INTERVAL * INTERVAL); i++) {

            // Randomly generated x and y values in the range [-1,1]
            rand_x = Math.random()*2-1;
            rand_y = Math.random()*2-1;

            // Distance between (x, y) from the origin
            origin_dist = rand_x * rand_x + rand_y * rand_y;

            // Checking if (x, y) lies inside the define
            // circle with R=1
            if (origin_dist <= 1)
                circle_points++;

            // Total number of points generated
            square_points++;

            // estimated pi after this iteration
            pi = ((4.0 * circle_points) / square_points);

            // For visual understanding (Optional)
            //System.out.println(rand_x+" "+rand_y+" "+circle_points+" "+square_points+" - "+pi);
        }

        // Final Estimated Value
        System.out.println("Final Estimation of Pi = " + pi);
    }
}

// This code is contributed by shruti456rawal

Python

import random

INTERVAL = 1000

circle_points = 0
square_points = 0

# Total Random numbers generated= possible x
# values* possible y values
for i in range(INTERVAL**2):

    # Randomly generated x and y values from a
    # uniform distribution
    # Range of x and y values is -1 to 1
    rand_x = random.uniform(-1, 1)
    rand_y = random.uniform(-1, 1)

    # Distance between (x, y) from the origin
    origin_dist = rand_x**2 + rand_y**2

    # Checking if (x, y) lies inside the circle
    if origin_dist <= 1:
        circle_points += 1

    square_points += 1

    # Estimating value of pi,
    # pi= 4*(no. of points generated inside the
    # circle)/ (no. of points generated inside the square)
    pi = 4 * circle_points / square_points

##    print(rand_x, rand_y, circle_points, square_points, "-", pi)
# print("\n")

print("Final Estimation of Pi=", pi)

C#

// C# program for estimation of Pi using Monte
// Carlo Simulation
using System;
using System.Collections.Generic;

class GFG
{

  // Defines precision for x and y values. More the
  // interval, more the number of significant digits
  static int INTERVAL = 10000;

  // Driver code
  public static void Main(string[] args)
  {

    // Instantiate random number generator using
    // system-supplied value as seed
    var rand = new Random();
    double rand_x, rand_y, origin_dist, pi = 0;
    int circle_points = 0, square_points = 0;

    // Total Random numbers generated = possible x
    // values * possible y values
    for (int i = 0; i < (INTERVAL * INTERVAL); i++) {

      // Randomly generated x and y values in the
      // range [-1,1]
      rand_x = (double)(rand.Next() % (INTERVAL + 1))
        / INTERVAL;
      rand_y = (double)(rand.Next() % (INTERVAL + 1))
        / INTERVAL;

      // Distance between (x, y) from the origin
      origin_dist = rand_x * rand_x + rand_y * rand_y;

      // Checking if (x, y) lies inside the define
      // circle with R=1
      if (origin_dist <= 1)
        circle_points++;

      // Total number of points generated
      square_points++;

      // estimated pi after this iteration
      pi = ((4.0 * circle_points) / square_points);

      // For visual understanding (Optional)
      // System.out.println(rand_x+" "+rand_y+"
      // "+circle_points+" "+square_points+" - "+pi);
    }

    // Final Estimated Value
    Console.WriteLine("Final Estimation of Pi = " + pi);
  }
}

// This code is contributed by phasing17

Javascript

/* JavaScript program for estimation of Pi using Monte
   Carlo Simulation */

// Defines precision for x and y values. More the
// interval, more the number of significant digits
let INTERVAL = 10000

    let interval,
    i;
let rand_x, rand_y, origin_dist, pi;
let circle_points = 0, square_points = 0;

// Total Random numbers generated = possible x
// values * possible y values
for (i = 0; i < (INTERVAL * INTERVAL); i++) {

    // Randomly generated x and y values
    rand_x = (Math.random() * (INTERVAL)) / INTERVAL;
    rand_y = (Math.random() * (INTERVAL)) / INTERVAL;

    // Distance between (x, y) from the origin
    origin_dist = rand_x * rand_x + rand_y * rand_y;

    // Checking if (x, y) lies inside the define
    // circle with R=1
    if (origin_dist <= 1)
        circle_points++;

    // Total number of points generated
    square_points++;

    // estimated pi after this iteration
    pi = (4 * circle_points) / square_points;

    // For visual understanding (Optional)
    // console.log(rand_x,  rand_y , circle_points,
    // square_points, "-", pi)
}

// Final Estimated Value
console.log("\nFinal Estimation of Pi = " + pi);

// This code is contributed by phasing17

Output:

Final Estimation of Pi = 3.16116

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.