Dynamic Programming (DP) and Directed Acyclic Graphs (DAG)
Last Updated :
07 Mar, 2024
Pre-Requisite:
What is Directed Graph? | Directed Graph meaning
Dynamic Programming (DP) Tutorial with Problems
Every Dynamic Programming problem can be represented as a Directed Acyclic Graph(DAG). The nodes of the DAG represent the subproblems and the edges represents the transitions between the subproblems.

1. Subproblems and DAG Nodes:
- Dynamic Programming involves breaking down a problem into similar subproblems and these subproblems are solved independently and their result is used to solve the original problem.
- Nodes of Directed Acyclic Graph represents the subproblems. We can also say these nodes represent a state.
2. Transitions and DAG Edges:
- Like the Nodes represents subproblems in the DAG, similarly the edges represent transition.
- The transition from one subproblem to another is represented by an edge.
3. Cycles and Redundancy:
- The reason it’s a directed acyclic graph is that if there are cycles in the directed graph then some states would lead back to themselves after a series of transitions leading to redundancy.
Let’s take an example to understand the above points:
Problem: Finding Longest Path in Directed Acyclic Graphs (DAG):
The dp state and the transition in this case will be:
Let dp[v] denote the length of the longest path ending at the node v. Initialize all the positions in dp array as 1. Clearly,
For every edge from node u to node v, dp[v] = max (dp[u]+1)
At the end check for the maximum value in dp[] array, which will be the longest path in the DAG.
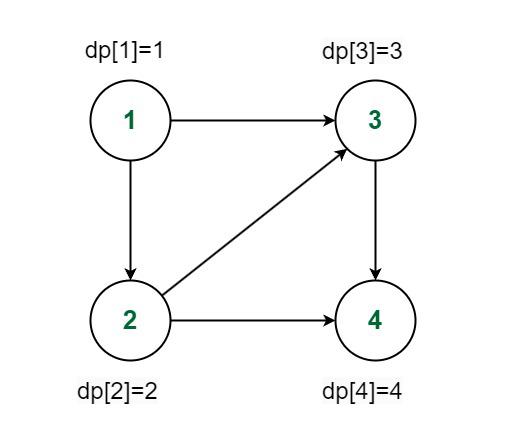
DP on Directed Graphs
What happens when the graph is not Directed Acyclic Graphs (DAG)?
If the graph contains a cycle, then some states would lead back to themselves after a series of transitions. This would lead to infinite calculations. Thus, answer will not exist if the graph is cyclic in this case. As shown in below image, we potentially keep traversing the cycle indefinitely, making it impossible to find the longest path.
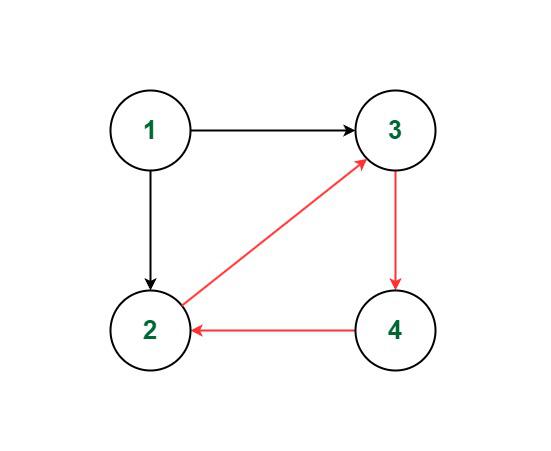
DP on Directed Graphs
How to Solve Dynamic Programming (DP) Problems on Directed Graphs:
Let us consider few problems which will tell how to define the states and make the transition:
Count the number of different ways to reach a node:
Given a Directed Acyclic Graph consisting of N nodes and M edges. The task is to determine the number of different ways to reach Node N from Node 1.
Solution: The problem can be solved in following steps:
1. Define the States: As mentioned above each Nodes of Directed Acyclic Graph represents a state. Let dp[v] be the number of ways to reach Node N from the vertex v.
2. Make the Transitions: Like the Nodes represents states in the DAG, similarly the edges represent transition. Thus dp[v] can be calculated by:
dp[v] = Σdp[u], for every edge v->u
3. Topological Consideration: We process the nodes topologically i.e., if edge v->u exists then dp[u] should be computed before dp[v].
Hence ,dp[1] will be our final answer.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int dfs(int n, vector<vector<int> >& adj, vector<int>& dp,
vector<int>& vis, int curr)
{
if (vis[curr] == 1)
return dp[curr];
vis[curr] = 1;
for (auto x : adj[curr]) {
if (!vis[x]) {
dfs(n, adj, dp, vis, x);
}
dp[curr] += dp[x];
}
return dp[curr];
}
int noOfWays(int n, vector<vector<int> >& edges)
{
vector<vector<int> > adj(n + 1);
for (vector<int> i : edges) {
adj[i[0]].push_back(i[1]);
}
vector<int> dp(n + 1, 0);
vector<int> vis(n + 1, 0);
dp[n] = 1;
vis[n] = 1;
int res = dfs(n, adj, dp, vis, 1);
return res;
}
int main()
{
int N = 5;
vector<vector<int> > edges = {
{ 1, 2 }, { 1, 3 }, { 2, 4 }, { 3, 4 }, { 4, 5 }
};
int result = noOfWays(N, edges);
cout << "No. of ways to reach Node N from Node 1: "
<< result << endl;
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.List;
public class WaysToReachNodeN {
private static int dfs(int n, List<List<Integer>> adj, int[] dp,
int[] vis, int curr) {
if (vis[curr] == 1)
return dp[curr];
vis[curr] = 1;
for (int x : adj.get(curr)) {
if (vis[x] == 0) {
dfs(n, adj, dp, vis, x);
}
dp[curr] += dp[x];
}
return dp[curr];
}
private static int noOfWays(int n, List<List<Integer>> edges) {
List<List<Integer>> adj = new ArrayList<>(n + 1);
for (int i = 0; i <= n; i++) {
adj.add(new ArrayList<>());
}
for (List<Integer> edge : edges) {
adj.get(edge.get(0)).add(edge.get(1));
}
int[] dp = new int[n + 1];
int[] vis = new int[n + 1];
dp[n] = 1;
vis[n] = 1;
int res = dfs(n, adj, dp, vis, 1);
return res;
}
public static void main(String[] args) {
int N = 5;
List<List<Integer>> edges = List.of(
List.of(1, 2), List.of(1, 3), List.of(2, 4), List.of(3, 4), List.of(4, 5)
);
int result = noOfWays(N, edges);
System.out.println("No. of ways to reach Node N from Node 1: " + result);
}
}
|
C#
using System;
using System.Collections.Generic;
class Program
{
static int DFS(int n, List<List<int>> adj, List<int> dp,
List<int> vis, int curr)
{
if (vis[curr] == 1)
return dp[curr];
vis[curr] = 1;
foreach (int x in adj[curr])
{
if (vis[x] == 0)
DFS(n, adj, dp, vis, x);
dp[curr] += dp[x];
}
return dp[curr];
}
static int NoOfWays(int n, List<List<int>> edges)
{
List<List<int>> adj = new List<List<int>>(n + 1);
for (int i = 0; i <= n; i++)
{
adj.Add(new List<int>());
}
foreach (List<int> i in edges)
{
adj[i[0]].Add(i[1]);
}
List<int> dp = new List<int>(new int[n + 1]);
List<int> vis = new List<int>(new int[n + 1]);
dp[n] = 1;
vis[n] = 1;
int res = DFS(n, adj, dp, vis, 1);
return res;
}
static void Main()
{
int N = 5;
List<List<int>> edges = new List<List<int>>
{
new List<int> {1, 2},
new List<int> {1, 3},
new List<int> {2, 4},
new List<int> {3, 4},
new List<int> {4, 5}
};
int result = NoOfWays(N, edges);
Console.WriteLine($"No. of ways to reach Node N from Node 1: {result}");
}
}
|
Javascript
function dfs(n, adj, dp, vis, curr) {
if (vis[curr] === 1)
return dp[curr];
vis[curr] = 1;
for (let x of adj[curr]) {
if (vis[x] === 0) {
dfs(n, adj, dp, vis, x);
}
dp[curr] += dp[x];
}
return dp[curr];
}
function noOfWays(n, edges) {
let adj = new Array(n + 1).fill().map(() => []);
for (let edge of edges) {
adj[edge[0]].push(edge[1]);
}
let dp = new Array(n + 1).fill(0);
let vis = new Array(n + 1).fill(0);
dp[n] = 1;
vis[n] = 1;
let res = dfs(n, adj, dp, vis, 1);
return res;
}
let N = 5;
let edges = [
[1, 2], [1, 3], [2, 4], [3, 4], [4, 5]
];
let result = noOfWays(N, edges);
console.log("No. of ways to reach Node N from Node 1:", result);
|
Python3
from collections import defaultdict
def dfs(n, adj, dp, vis, curr):
if vis[curr] == 1:
return dp[curr]
vis[curr] = 1
for x in adj[curr]:
if vis[x] == 0:
dfs(n, adj, dp, vis, x)
dp[curr] += dp[x]
return dp[curr]
def no_of_ways(n, edges):
adj = defaultdict(list)
for edge in edges:
adj[edge[0]].append(edge[1])
dp = [0] * (n + 1)
vis = [0] * (n + 1)
dp[n] = 1
vis[n] = 1
res = dfs(n, adj, dp, vis, 1)
return res
N = 5
edges = [
(1, 2), (1, 3), (2, 4), (3, 4), (4, 5)
]
result = no_of_ways(N, edges)
print("No. of ways to reach Node N from Node 1:", result)
|
Output
No. of ways to reach Node N from Node 1: 2
Time Complexity: O(N), Where ‘N’ is the number of nodes in the given graph.
Auxiliary Space: O(N)
Find the largest number of nodes colored with the most occurring color on any path of DAG:
Given a Directed Acyclic Graph consisting of N nodes and M edges. Each node is assigned a lowercase alphabet representing the color of that node (‘a’ to ‘z’). The task is to determine the largest value of any path. The value of a path is defined as the number of nodes which are colored with the most occurring color in the path.
Solution: The problem can be solved in following steps:
1. Define the States: We can observe that there are total 26 colors possible. So, we can make a 2D dp[][] array of size N*26. Let dp[v][i] represent the maximum count of vertices having color i of any path starting from vertex v.
2. Make the Transitions: Again, like the Nodes represent states in the DAG, similarly the edges represent transitions. Thus dp[v][i] can be calculated by:
dp[v][i] = max(dp[u][i]+col, dp[v][i]), for each edge v->u and each color i from 0 to 25. The value of col will be 1 if color of vertex v is equal to i otherwise it will be 0.
3. Topological Consideration: Again, we process the nodes topologically i.e., if edge v->u exists then the node u should be processed before node v.
Hence, our final answer will be maximum of dp[v][i] for each vertex from 1 to N and color from 0 to 25.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void dfs(int n, vector<vector<int>>& adj, vector<vector<int>>& dp,
vector<int>& vis, int curr, string& s) {
if (vis[curr] == 1)
return;
vis[curr] = 1;
dp[curr][s[curr - 1] - 97] = 1;
for (auto x : adj[curr]) {
if (!vis[x]) {
dfs(n, adj, dp, vis, x, s);
}
for (int j = 0; j < 26; j++) {
int col = 0;
if (s[curr - 1] - 97 == j)
col = 1;
dp[curr][j] = max(dp[curr][j], dp[x][j] + col);
}
}
}
int maxcolorpath(int n, vector<vector<int>>& edges, string s) {
vector<vector<int>> adj(n + 1);
for (vector<int> i : edges) {
adj[i[0]].push_back(i[1]);
}
vector<vector<int>> dp(n + 1, vector<int>(26, 0));
vector<int> vis(n + 1);
dfs(n, adj, dp, vis, 1, s);
int res = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 26; j++) {
res = max(res, dp[i][j]);
}
}
return res;
}
int main() {
int N = 5;
vector<vector<int>> edges = {
{1, 2}, {1, 3}, {2, 4}, {3, 4}, {4, 5}
};
string color = "abaca";
int result = maxcolorpath(N, edges, color);
cout << "Maximum count of vertices having the most occurring color: "
<< result << endl;
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.Arrays;
public class MaxColorPath {
static void dfs(int n, ArrayList<ArrayList<Integer>> adj, int[][] dp,
int[] vis, int curr, String s) {
if (vis[curr] == 1)
return;
vis[curr] = 1;
dp[curr][s.charAt(curr - 1) - 'a'] = 1;
for (int x : adj.get(curr)) {
if (vis[x] == 0) {
dfs(n, adj, dp, vis, x, s);
}
for (int j = 0; j < 26; j++) {
int col = (s.charAt(curr - 1) - 'a' == j) ? 1 : 0;
dp[curr][j] = Math.max(dp[curr][j], dp[x][j] + col);
}
}
}
static int maxColorPath(int n, int[][] edges, String s) {
ArrayList<ArrayList<Integer>> adj = new ArrayList<>(n + 1);
for (int i = 0; i <= n; i++) {
adj.add(new ArrayList<>());
}
for (int[] edge : edges) {
adj.get(edge[0]).add(edge[1]);
}
int[][] dp = new int[n + 1][26];
int[] vis = new int[n + 1];
dfs(n, adj, dp, vis, 1, s);
int res = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 26; j++) {
res = Math.max(res, dp[i][j]);
}
}
return res;
}
public static void main(String[] args) {
int N = 5;
int[][] edges = {
{1, 2}, {1, 3}, {2, 4}, {3, 4}, {4, 5}
};
String color = "abaca";
int result = maxColorPath(N, edges, color);
System.out.println("Maximum count of vertices having the most occurring color: " + result);
}
}
|
C#
using System;
using System.Collections.Generic;
using System.Linq;
class Program
{
static void Dfs(int n, List<int>[] adj, int[][] dp, int[] vis, int curr, string s)
{
if (vis[curr] == 1)
return;
vis[curr] = 1;
dp[curr][s[curr - 1] - 97] = 1;
foreach (var x in adj[curr])
{
if (vis[x] == 0)
{
Dfs(n, adj, dp, vis, x, s);
}
for (int j = 0; j < 26; j++)
{
int col = 0;
if (s[curr - 1] - 97 == j)
col = 1;
dp[curr][j] = Math.Max(dp[curr][j], dp[x][j] + col);
}
}
}
static int MaxColorPath(int n, int[][] edges, string s)
{
var adj = new List<int>[n + 1];
for (int i = 0; i < adj.Length; i++)
{
adj[i] = new List<int>();
}
foreach (var i in edges)
{
adj[i[0]].Add(i[1]);
}
var dp = new int[n + 1][];
for (int i = 0; i < dp.Length; i++)
{
dp[i] = new int[26];
}
var vis = new int[n + 1];
Dfs(n, adj, dp, vis, 1, s);
int res = 0;
for (int i = 1; i <= n; i++)
{
for (int j = 0; j < 26; j++)
{
res = Math.Max(res, dp[i][j]);
}
}
return res;
}
static void Main()
{
int N = 5;
int[][] edges = {
new int[] {1, 2}, new int[] {1, 3}, new int[] {2, 4}, new int[] {3, 4}, new int[] {4, 5}
};
string color = "abaca";
int result = MaxColorPath(N, edges, color);
Console.WriteLine("Maximum count of vertices having the most occurring color: "
+ result);
}
}
|
Javascript
function dfs(n, adj, dp, vis, curr, s) {
if (vis[curr] === 1)
return;
vis[curr] = 1;
dp[curr][s.charCodeAt(curr - 1) - 97] = 1;
for (let x of adj[curr]) {
if (!vis[x]) {
dfs(n, adj, dp, vis, x, s);
}
for (let j = 0; j < 26; j++) {
let col = 0;
if (s.charCodeAt(curr - 1) - 97 === j)
col = 1;
dp[curr][j] = Math.max(dp[curr][j], dp[x][j] + col);
}
}
}
function maxcolorpath(n, edges, s) {
let adj = new Array(n + 1).fill(null).map(() => []);
for (let i of edges) {
adj[i[0]].push(i[1]);
}
let dp = new Array(n + 1).fill(null).map(() => new Array(26).fill(0));
let vis = new Array(n + 1).fill(0);
dfs(n, adj, dp, vis, 1, s);
let res = 0;
for (let i = 1; i <= n; i++) {
for (let j = 0; j < 26; j++) {
res = Math.max(res, dp[i][j]);
}
}
return res;
}
let N = 5;
let edges = [
[1, 2], [1, 3], [2, 4], [3, 4], [4, 5]
];
let color = "abaca";
let result = maxcolorpath(N, edges, color);
console.log("Maximum count of vertices having the most occurring color: " + result);
|
Python3
def dfs(n, adj, dp, vis, curr, s):
if vis[curr] == 1:
return
vis[curr] = 1
dp[curr][ord(s[curr - 1]) - 97] = 1
for x in adj[curr]:
if not vis[x]:
dfs(n, adj, dp, vis, x, s)
for j in range(26):
col = 0
if ord(s[curr - 1]) - 97 == j:
col = 1
dp[curr][j] = max(dp[curr][j], dp[x][j] + col)
def maxcolorpath(n, edges, s):
adj = [[] for _ in range(n + 1)]
for i in edges:
adj[i[0]].append(i[1])
dp = [[0] * 26 for _ in range(n + 1)]
vis = [0] * (n + 1)
dfs(n, adj, dp, vis, 1, s)
res = 0
for i in range(1, n + 1):
for j in range(26):
res = max(res, dp[i][j])
return res
N = 5
edges = [
[1, 2], [1, 3], [2, 4], [3, 4], [4, 5]
]
color = "abaca"
result = maxcolorpath(N, edges, color)
print("Maximum count of vertices having the most occurring color:", result)
|
Output
Maximum count of vertices having the most occurring color: 3
Time Complexity: O(N), Where ‘N’ is the number of nodes in the given graph.
Auxiliary Space: O(N)
Practice Problems Dynamic Programming (DP) on Directed Graphs for Competitive Programming:
Share your thoughts in the comments
Please Login to comment...