Dixon’s Factorization Method with implementation
Last Updated :
05 Mar, 2023
Dixon’s Factorization method is an integer factorization algorithm. In this article, this method is explained to find the factors of a composite number. Dixon Factorization is based on the well-known fact of number theory that:
- If
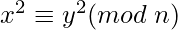 with
with 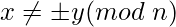 it is likely that gcd(x – y, n) will be factor of n.
it is likely that gcd(x – y, n) will be factor of n.
For example:
if N = 84923, by starting at 292, the first number greater than √N and counting up 5052 mod 84923 = 256 = 162 So (505 – 16)(505 + 16) = 0 mod 84923. Computing the greatest common divisor of 505 – 16 and N using Euclid’s algorithm gives 163, which is a factor of N.
Dixon’s Factorization Algorithm:
- Step 1: Choose a bound B and identify the factor base (P) of all primes less than or equal to B.
- Step 2: Search for positive integer z, such that
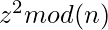 is B-Smooth.
is B-Smooth. (1) 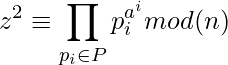
B-Smooth: A positive integer is called B-Smooth if none of its prime factors is greater than B. For example:
720 has prime factorization as 24 * 32 * 51 Therefore 720 is 5 smooth because none of its prime factors is greater than 5.
- Step 3: After generating enough of these relations (generally few more than the size of P), we use the method of linear algebra (e.g Gaussian Elimination) to multiply together these relations. Repeat this step until we formed a sufficient number of smooth squares.
- Step 4: After multiplying all these relations, we get the final equation say:
a2 = b2 mod(N)
- Step 5: Therefore, the factors of the above equation can be determined as:
GCD(a - b, N), GCD(a + b, N)
Step by Step execution of the Dixon’s Factorization Algorithm:
- Let’s say, we want to factor N = 23449 using bound B = 7. Therefore, the factor base P = {2, 3, 5, 7}.
- Here, x = ceil(sqrt(n)) = 154. So, we search randomly for integers between 154 and N whose squares are B-Smooth.
- As mentioned before, a positive integer is called B-Smooth if none of its prime factors is greater than B. So, let’s say, we find two numbers which are 970 and 8621 such that their none of their squares have prime factors greater than 7.
- Starting here the first related squares we get are:
- 9702 % 23499 = 2940 = 22 * 3 * 5 * 72
- 86212 % 23499 = 11760 = 24 * 3 * 5 * 72
- So, (970 * 8621)2 = (23 * 3 * 5 * 72)2 % 23499. That is: 142562 = 58802 % 23499.
- Now, we find:
gcd(14256 - 5880, 23449) = 131
gcd(14256 + 5880, 23449) = 179
- Therefore, the factors are: N = 131 * 179
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
#include<vector>
void factor(int n)
{
int base[4] = {2, 3, 5, 7};
int start = int(sqrt(n));
vector<vector<int> >pairs;
int len=sizeof(base)/sizeof(base[0]);
for(int i = start; i < n; i++)
{
vector<int> v;
for(int j = 0; j < len; j++)
{
int lhs = ((int)pow(i,2))% n;
int rhs = ((int)pow(base[j],2)) % n;
if(lhs == rhs)
{
v.push_back(i);
v.push_back(base[j]);
pairs.push_back(v);
}
}
}
vector<int>newvec;
len = pairs.size();
for (int i = 0; i < len;i++){
int factor = __gcd(pairs[i][0] - pairs[i][1], n);
if(factor != 1)
newvec.push_back(factor);
}
set<int>s;
for (int i = 0; i < newvec.size(); i++)
s.insert(newvec[i]);
for(auto i = s.begin(); i != s.end(); i++)
cout<<(*i)<<" ";
}
int main()
{
factor(23449);
}
|
Java
import java.util.*;
class GFG {
static int gcd(int num1, int num2)
{
int a = Math.abs(num1);
int b = Math.abs(num2);
while ((a != 0) && (b != 0) && (a != b)) {
if (a > b) {
a = a - b;
}
else {
b = b - a;
};
};
return a | b;
}
static void factor(int n)
{
int[] base1 = { 2, 3, 5, 7 };
int start = (int)(Math.sqrt(n));
int len = base1.length;
ArrayList<ArrayList<Integer> > pairs
= new ArrayList<ArrayList<Integer> >();
for (int i = start; i < n; i++) {
for (int j = 0; j < len; j++) {
int lhs = ((int)Math.pow(i, 2)) % n;
int rhs = ((int)Math.pow(base1[j], 2)) % n;
if (lhs == rhs) {
ArrayList<Integer> l1
= new ArrayList<Integer>();
l1.add(i);
l1.add(base1[j]);
pairs.add(l1);
}
}
}
ArrayList<Integer> newvec
= new ArrayList<Integer>();
len = pairs.size();
for (int i = 0; i < len; i++) {
int factor = gcd(pairs.get(i).get(0)
- pairs.get(i).get(1),
n);
if (factor != 1)
newvec.add(factor);
}
HashSet<Integer> s = new HashSet<Integer>();
for (int i = 0; i < newvec.size(); i++)
s.add(newvec.get(i));
for (int s1 : s)
System.out.print(s1 + " ");
}
public static void main(String[] args)
{
factor(23449);
}
}
|
Python3
from math import sqrt, gcd
import numpy as np
def factor(n):
base = [2, 3, 5, 7]
start = int(sqrt(n))
pairs = []
for i in range(start, n):
for j in range(len(base)):
lhs = i**2 % n
rhs = base[j]**2 % n
if(lhs == rhs):
pairs.append([i, base[j]])
new = []
for i in range(len(pairs)):
factor = gcd(pairs[i][0] - pairs[i][1], n)
if(factor != 1):
new.append(factor)
x = np.array(new)
return(np.unique(x))
if __name__ == "__main__":
print(factor(23449))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int gcd (int num1, int num2) {
int a = Math.Abs(num1);
int b = Math.Abs(num2);
while ( (a != 0) && (b != 0) && (a != b)) {
if(a > b){
a = a - b;
}else{
b = b - a;
};
};
return a | b;
}
static void factor(int n)
{
int[] base1 = {2, 3, 5, 7};
int start = (int)(Math.Sqrt(n));
List<int []> pairs = new List<int []>();
int len= base1.Length;
for(int i = start; i < n; i++)
{
List<int> v = new List<int>();
for(int j = 0; j < len; j++)
{
int lhs = ((int)Math.Pow(i, 2)) % n;
int rhs = ((int)Math.Pow(base1[j], 2)) % n;
if(lhs == rhs)
{
pairs.Add(new [] {i, base1[j]});
}
}
}
List<int> newvec = new List<int>();
len = pairs.Count;
for (int i = 0; i < len;i++){
int factor = gcd(pairs[i][0] - pairs[i][1], n);
if(factor != 1)
newvec.Add(factor);
}
HashSet<int> s = new HashSet<int>();
for (int i = 0; i < newvec.Count; i++)
s.Add(newvec[i]);
foreach (var s1 in s)
Console.Write(s1 + " ");
}
public static void Main(string[] args)
{
factor(23449);
}
}
|
Javascript
const gcd = (num1, num2) => {
let a = Math.abs(num1);
let b = Math.abs(num2);
while (a && b && a !== b) {
if(a > b){
[a, b] = [a - b, b];
}else{
[a, b] = [a, b - a];
};
};
return a || b;
};
function factor(n)
{
let base = [2, 3, 5, 7];
let start = Math.floor(Math.sqrt(n));
let pairs = [];
let len= base.length;
for(let i = start; i < n; i++)
{
let v = [];
for(let j = 0; j < len; j++)
{
let lhs = (i ** 2)% n;
let rhs = ((base[j] ** 2)) % n;
if(lhs == rhs)
{
pairs.push([i, base[j]]);
}
}
}
let newvec = [];
len = pairs.length;
for (let i = 0; i < len;i++){
let factor = gcd(pairs[i][0] - pairs[i][1], n);
if(factor != 1)
newvec.push(factor);
}
let s = new Set();
for (let i = 0; i < newvec.length; i++)
s.add(newvec[i]);
console.log(s)
}
factor(23449);
|
Time Complexity : O(sqrt(N))
Space complexity : O(B)
Share your thoughts in the comments
Please Login to comment...