Wheel Factorization Algorithm

Given a number N. The task is to check if the given number is Prime Number or not.
Examples:

Input: N = 987 
Output: Not a Prime Number 
Explanation:
As, 987 = 3*7*47. Therefore 987 is not a prime number.
Input: N = 67 
Output: Prime Number 

Wheel Factorization Method:
Wheel Factorization is the improvement of the method Sieve of Eratosthenes. For wheel factorization, one starts from a small list of numbers, called the basis — generally the first few prime numbers, then one generates the list, called the wheel, of the integers that are coprime with all numbers of the basis. Then to find the smallest divisor of the number to be factorized, one divides it successively by the numbers on the basis, and in the wheel. 

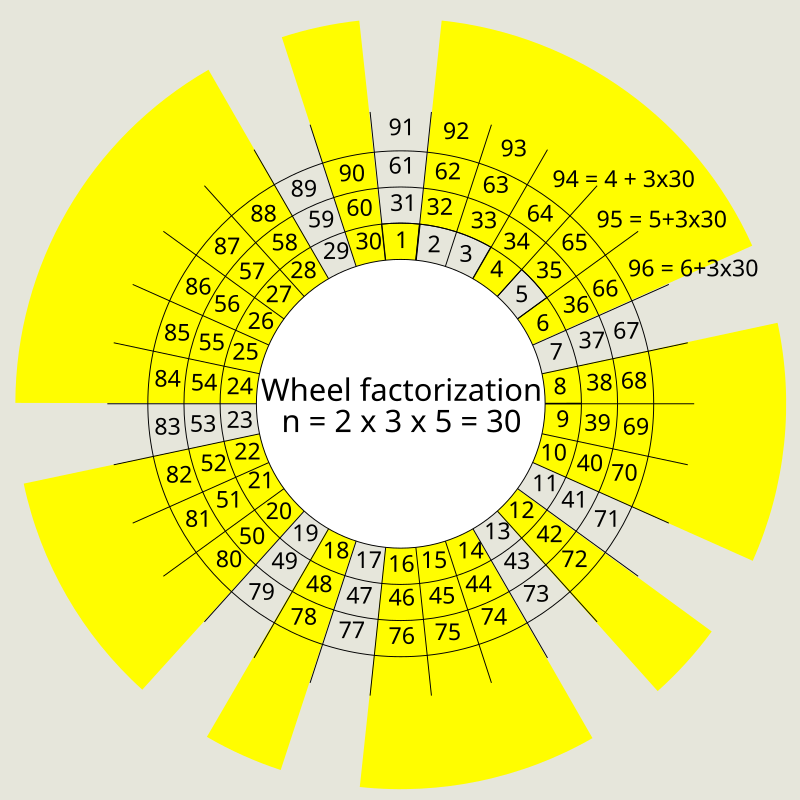
Let say we select basis as {2, 3, 5} and the numbers which are coprime to the basis are {7, 11, 13, 17, 19, 23, 29, 31} are set as the wheel. 
To understand it more, see the pattern in the above image that the numbers exhibit. The LCM of the first three Prime Numbers is 30. The numbers(less than 30) which are ending with 7, 1, and 3 and are not a multiple of 2, 3, and 5 and are always prime i.e {7, 11, 13, 17, 19, 23, 29}. Adding the no. 31 to this list and then if we add multiples of 30 to any of the numbers in the list, it gives us a Prime Number. 
Algorithm for Wheel Factorization Method:

For the number N to be Prime or not:
bool isPrime(x) {
    if (x < 2) {
          return False;
    }
    for N in {2, 3, 5} {
          return False;
    }
    for p= [0, sqrt(N)] such that p = p + 30: {
          for c in [p+7, p+11, p+13, p+17, p+19, p+23, p+29, p+31] {
              if c > sqrt(N)      
                  break;
              else if N % (c+p) = 0:
                  return False;
          }
    }
}
return True;
}

Approach:
Following is the approach for the above algorithm: 

1. For Primality Test of a given Number N, check if the given number is divisible by any of the number 2, 3, 5 or not.
2. If the number is not divisible by any of 2, 3, 5, then check if the number formed by adding multiples of 30 in the list [7, 11, 13, 17, 19, 23, 29, 31] divides the given number N or not. If Yes then the given number is not Prime Number, else it is a Prime Number.

Below is the implementation of the above approach: 

C++

// C++ program to check if the
// given number is prime using
// Wheel Factorization Method
#include "bits/stdc++.h"
using namespace std;

// Function to check if a given
// number x is prime or not
void isPrime(int N)
{
    bool isPrime = true;
    // The Wheel for checking
    // prime number
    int arr[8] = { 7, 11, 13, 17,
                   19, 23, 29, 31 };

    // Base Case
    if (N < 2) {
        isPrime = false;
    }

    // Check for the number taken
    // as basis
    if (N % 2 == 0 || N % 3 == 0
        || N % 5 == 0) {
        isPrime = false;
    }

    // Check for Wheel
    // Here i, acts as the layer
    // of the wheel
    for (int i = 0; i < sqrt(N); i += 30) {

        // Check for the list of
        // Sieve in arr[]
        for (int c : arr) {

            // If number is greater
            // than sqrt(N) break
            if (c > sqrt(N)) {
                break;
            }

            // Check if N is a multiple
            // of prime number in the
            // wheel
            else {
                if (N % (c + i) == 0) {
                    isPrime = false;
                    break;
                }
            }

            // If at any iteration
            // isPrime is false,
            // break from the loop
            if (!isPrime)
                break;
        }
    }

    if (isPrime)
        cout << "Prime Number";
    else
        cout << "Not a Prime Number";
}

// Driver's Code
int main()
{
    int N = 121;

    // Function call for primality
    // check
    isPrime(N);
    return 0;
}

Java

// Java program to check if the
// given number is prime using
// Wheel Factorization Method
import java.util.*;

class GFG{

// Function to check if a given
// number x is prime or not
static void isPrime(int N)
{
    boolean isPrime = true;

        // The Wheel for checking
    // prime number
    int []arr = { 7, 11, 13, 17,19, 23, 29, 31 };

    // Base Case
    if (N < 2) {
        isPrime = false;
    }

    // Check for the number taken
    // as basis
    if (N % 2 == 0 || N % 3 == 0
        || N % 5 == 0) {
        isPrime = false;
    }

    // Check for Wheel
    // Here i, acts as the layer
    // of the wheel
    for (int i = 0; i < Math.sqrt(N); i += 30) {

        // Check for the list of
        // Sieve in arr[]
        for (int c : arr) {

            // If number is greater
            // than sqrt(N) break
            if (c > Math.sqrt(N)) {
                break;
            }

            // Check if N is a multiple
            // of prime number in the
            // wheel
            else {
                if (N % (c + i) == 0) {
                    isPrime = false;
                    break;
                }
            }

            // If at any iteration
            // isPrime is false,
            // break from the loop
            if (!isPrime)
                break;
        }
    }

    if (isPrime)
        System.out.println("Prime Number");
    else
        System.out.println("Not a Prime Number");
}

// Driver's Code
public static void main(String args[])
{
    int N = 121;

    // Function call for primality
    // check
    isPrime(N);
}
}

// This code is contributed by Surendra_Gangwar

C#

// C# program to check if the
// given number is prime using
// Wheel Factorization Method
using System;

class GFG{

// Function to check if a given
// number x is prime or not
static void isPrime(int N)
{
    bool isPrime = true;

     // The Wheel for checking
    // prime number
    int []arr = { 7, 11, 13, 17,19, 23, 29, 31 };

    // Base Case
    if (N < 2) {
        isPrime = false;
    }

    // Check for the number taken
    // as basis
    if (N % 2 == 0 || N % 3 == 0
        || N % 5 == 0) {
        isPrime = false;
    }

    // Check for Wheel
    // Here i, acts as the layer
    // of the wheel
    for (int i = 0; i < (int)Math.Sqrt(N); i += 30) {

        // Check for the list of
        // Sieve in arr[]
        foreach (int c in arr) {

            // If number is greater
            // than sqrt(N) break
            if (c > (int)Math.Sqrt(N)) {
                break;
            }

            // Check if N is a multiple
            // of prime number in the
            // wheel
            else {
                if (N % (c + i) == 0) {
                    isPrime = false;
                    break;
                }
            }

            // If at any iteration
            // isPrime is false,
            // break from the loop
            if (!isPrime)
                break;
        }
    }

    if (isPrime)
        Console.WriteLine("Prime Number");
    else
        Console.WriteLine("Not a Prime Number");
}

// Driver's Code
public static void Main(String []args)
{
    int N = 121;

    // Function call for primality
    // check
    isPrime(N);
}
}

// This code is contributed by Yash_R

Python3

# Python3  program to check if the
# given number is prime using
# Wheel Factorization Method
import math

# Function to check if a given
# number x is prime or not
def isPrime( N):

    isPrime = True;
    # The Wheel for checking
    # prime number
    arr= [ 7, 11, 13, 17,
                19, 23, 29, 31 ]

    # Base Case
    if (N < 2) :
        isPrime = False

    # Check for the number taken
    # as basis
    if (N % 2 == 0 or N % 3 == 0
        or N % 5 == 0):
        isPrime = False

    # Check for Wheel
    # Here i, acts as the layer
    # of the wheel
    for i in range(0,int(math.sqrt(N)), 30) :

        # Check for the list of
        # Sieve in arr[]
        for c in  arr:

            # If number is greater
            # than sqrt(N) break
            if (c > int(math.sqrt(N))):
                break

            # Check if N is a multiple
            # of prime number in the
            # wheel
            else :
                if (N % (c + i) == 0) :
                    isPrime = False
                    break

            # If at any iteration
            # isPrime is false,
            # break from the loop
            if (not isPrime):
                break

    if (isPrime):
        print("Prime Number")
    else:
        print("Not a Prime Number")

# Driver's Code
if __name__ == "__main__":
    N = 121

    # Function call for primality
    # check
    isPrime(N)

# This code is contributed by chitranayal

Javascript

<script>

// JavaScript program to check if the
// given number is prime using
// Wheel Factorization Method


// Function to check if a given
// number x is prime or not
function isPrime(N)
{
    let isPrime = true;
    // The Wheel for checking
    // prime number
    let arr = [ 7, 11, 13, 17,
                19, 23, 29, 31 ];

    // Base Case
    if (N < 2) {
        isPrime = false;
    }

    // Check for the number taken
    // as basis
    if (N % 2 == 0 || N % 3 == 0
        || N % 5 == 0) {
        isPrime = false;
    }

    // Check for Wheel
    // Here i, acts as the layer
    // of the wheel
    for (let i = 0; i < Math.sqrt(N); i += 30) {

        // Check for the list of
        // Sieve in arr[]
        for (let c of arr) {

            // If number is greater
            // than sqrt(N) break
            if (c > Math.sqrt(N)) {
                break;
            }

            // Check if N is a multiple
            // of prime number in the
            // wheel
            else {
                if (N % (c + i) == 0) {
                    isPrime = false;
                    break;
                }
            }

            // If at any iteration
            // isPrime is false,
            // break from the loop
            if (!isPrime)
                break;
        }
    }

    if (isPrime)
        document.write("Prime Number");
    else
        document.write("Not a Prime Number");
}

// Driver's Code


    let N = 121;

    // Function call for primality
    // check
    isPrime(N);


    // This code is contributed by _saurabh_jaiswal

</script>

Output:

Not a Prime Number

Time Complexity: O(N^3/2)

Auxiliary Space: O(1)