Difference Between sum of degrees of odd and even degree nodes in an Undirected Graph

Given an undirected graph with N vertices and M edges, the task is to find the absolute difference Between the sum of degrees of odd degree nodes and even degree nodes in an undirected Graph.

Examples:

Input: N = 4, edges[][] = { { 1, 2 }, { 1, 3 }, { 1, 4 }, { 2, 3 }, { 2, 4 }, { 3, 4 } } 
Output: 12 
Explanation:
Below is the graph for the above information:  

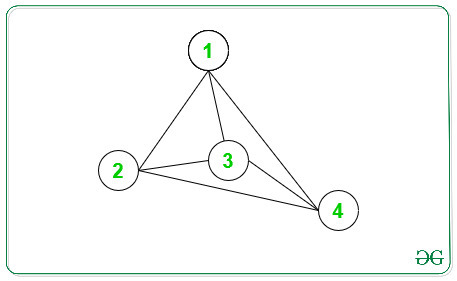
Node -> Degree 
1 -> 3 
2 -> 3 
3 -> 3 
4 -> 3
Sum of odd degree node = 3 + 3 + 3 + 3 = 12 
Sum of even degree node = 0 
Difference = 12

Input: N = 5, edges[][] = { { 1, 2 }, { 1, 3 }, { 2, 4 }, { 2, 5 } } 
Output: 4

Approach:

1. For each vertex, the degree can be calculated by the length of the Adjacency List of the given graph at the corresponding vertex.
2. Count the sum of degrees of odd degree nodes and even degree nodes and print the difference.

Below is the implementation of the above approach:

C++

// C++ implementation to print the
// Difference Between sum of degrees
// of odd degree nodes and even
// degree nodes.
#include <bits/stdc++.h>
using namespace std;

// Function to print the difference
// Between sum of degrees of odd
// degree nodes and even degree nodes.
int OddEvenDegree(int N, int M,
                    int edges[][2])
{
    // To store Adjacency List of
    // a Graph
    vector<int> Adj[N + 1];

    int EvenSum = 0;
    int OddSum = 0;

    // Make Adjacency List
    for (int i = 0 ; i < M ; i++) {
        int x = edges[i][0];
        int y = edges[i][1];

        Adj[x].push_back(y);
        Adj[y].push_back(x);
    }

    // Traverse each vertex
    for (int i = 1; i <= N; i++) {

        // Find size of Adjacency List
        int x = Adj[i].size();

        // If length of Adj[i] is
        // an odd number, add
        // length in OddSum
        if (x % 2 != 0)
        {
            OddSum += x;
        }
        else
        {
            // If length of Adj[i] is
            // an even number, add
            // length in EvenSum
            EvenSum += x;
        }

    }

    return abs(OddSum - EvenSum);
}

// Driver code
int main()
{
    // Vertices and Edges
    int N = 4, M = 6;

    // Edges
    int edges[M][2] = { { 1, 2 }, { 1, 3 }, { 1, 4 },
                       { 2, 3 }, { 2, 4 }, { 3, 4 } };

    // Function Call
    cout<< OddEvenDegree(N, M, edges);

    return 0;
}

Java

// Java implementation to print the
// difference between sum of degrees
// of odd degree nodes and even
// degree nodes.
import java.util.*;

class GFG{

// Function to print the difference
// between sum of degrees of odd
// degree nodes and even degree nodes.
static int OddEvenDegree(int N, int M,
                         int edges[][])
{

    // To store adjacency list
    // of a graph
    @SuppressWarnings("unchecked")
    Vector<Integer> []Adj = new Vector[N + 1];

    for(int i = 0; i < N + 1; i++)
    {
       Adj[i] = new Vector<Integer>();
    }

    int EvenSum = 0;
    int OddSum = 0;

    // Make adjacency list
    for(int i = 0; i < M; i++)
    {
       int x = edges[i][0];
       int y = edges[i][1];

       Adj[x].add(y);
       Adj[y].add(x);
    }

    // Traverse each vertex
    for(int i = 1; i <= N; i++)
    {

       // Find size of adjacency list
       int x = Adj[i].size();

       // If length of Adj[i] is
       // an odd number, add
       // length in OddSum
       if (x % 2 != 0)
       {
           OddSum += x;
       }
       else
       {

           // If length of Adj[i] is
           // an even number, add
           // length in EvenSum
           EvenSum += x;
       }
    }
    return Math.abs(OddSum - EvenSum);
}

// Driver code
public static void main(String[] args)
{

    // Vertices and edges
    int N = 4, M = 6;

    // Edges
    int edges[][] = { { 1, 2 }, { 1, 3 }, { 1, 4 },
                      { 2, 3 }, { 2, 4 }, { 3, 4 } };

    // Function call
    System.out.print(OddEvenDegree(N, M, edges));
}
}

// This code is contributed by PrinciRaj1992

Python3

# Python3 implementation to print the
# Difference Between sum of degrees
# of odd degree nodes and even
# degree nodes.

# Function to print the difference
# Between sum of degrees of odd
# degree nodes and even degree nodes.
def OddEvenDegree(N, M, edges):

    # To store Adjacency
    # List of a Graph
    Adj = [[] for i in range(N + 1)]

    EvenSum = 0;
    OddSum = 0;

    # Make Adjacency List
    for i in range(M):
        x = edges[i][0];
        y = edges[i][1];

        Adj[x].append(y);
        Adj[y].append(x);

    # Traverse each vertex
    for i in range(1, N + 1):

        # Find size of
        # Adjacency List
        x = len(Adj[i])

        # If length of Adj[i] is
        # an odd number, add
        # length in OddSum
        if (x % 2 != 0):
            OddSum += x;
        else:

            # If length of Adj[i] is
            # an even number, add
            # length in EvenSum
            EvenSum += x;

    return abs(OddSum - EvenSum);

# Driver code
if __name__ == "__main__":

    # Vertices and Edges
    N = 4
    M = 6

    # Edges
    edges = [[1, 2], [1, 3],
             [1, 4], [2, 3],
             [2, 4], [3, 4]]

    # Function Call
    print(OddEvenDegree(N, M,
                        edges));

# This code is contributed by rutvik_56

C#

// C# implementation to print the
// difference between sum of degrees
// of odd degree nodes and even
// degree nodes.
using System;
using System.Collections.Generic;
class GFG{

// Function to print the difference
// between sum of degrees of odd
// degree nodes and even degree nodes.
static int OddEvenDegree(int N, int M,
                         int [,]edges)
{
  // To store adjacency list
  // of a graph
  List<int> []Adj = new List<int>[N + 1];

  for(int i = 0; i < N + 1; i++)
  {
    Adj[i] = new List<int>();
  }

  int EvenSum = 0;
  int OddSum = 0;

  // Make adjacency list
  for(int i = 0; i < M; i++)
  {
    int x = edges[i, 0];
    int y = edges[i, 1];

    Adj[x].Add(y);
    Adj[y].Add(x);
  }

  // Traverse each vertex
  for(int i = 1; i <= N; i++)
  {
    // Find size of adjacency list
    int x = Adj[i].Count;

    // If length of Adj[i] is
    // an odd number, add
    // length in OddSum
    if (x % 2 != 0)
    {
      OddSum += x;
    }
    else
    {
      // If length of Adj[i] is
      // an even number, add
      // length in EvenSum
      EvenSum += x;
    }
  }
  return Math.Abs(OddSum - EvenSum);
}

// Driver code
public static void Main(String[] args)
{
  // Vertices and edges
  int N = 4, M = 6;

  // Edges
  int [,]edges = {{1, 2}, {1, 3}, {1, 4},
                  {2, 3}, {2, 4}, {3, 4}};

  // Function call
  Console.Write(OddEvenDegree(N, M, edges));
}
}

// This code is contributed by Princi Singh

Javascript

<script>

// Javascript implementation to print the
// Difference Between sum of degrees
// of odd degree nodes and even
// degree nodes.

// Function to print the difference
// Between sum of degrees of odd
// degree nodes and even degree nodes.
function OddEvenDegree(N, M, edges)
{
    // To store Adjacency List of
    // a Graph
    var Adj = Array.from(Array(N+1), ()=>Array());

    var EvenSum = 0;
    var OddSum = 0;

    // Make Adjacency List
    for (var i = 0 ; i < M ; i++) {
        var x = edges[i][0];
        var y = edges[i][1];

        Adj[x].push(y);
        Adj[y].push(x);
    }

    // Traverse each vertex
    for (var i = 1; i <= N; i++) {

        // Find size of Adjacency List
        var x = Adj[i].length;

        // If length of Adj[i] is
        // an odd number, add
        // length in OddSum
        if (x % 2 != 0)
        {
            OddSum += x;
        }
        else
        {
            // If length of Adj[i] is
            // an even number, add
            // length in EvenSum
            EvenSum += x;
        }

    }

    return Math.abs(OddSum - EvenSum);
}

// Driver code
// Vertices and Edges
var N = 4, M = 6;
// Edges
var edges = [ [ 1, 2 ], [ 1, 3 ], [ 1, 4 ],
                   [ 2, 3 ], [ 2, 4 ], [ 3, 4 ] ];
// Function Call
document.write( OddEvenDegree(N, M, edges));


</script>

Output

12